小型無人船阻力CFD模擬方法

肖國權，李天成，黎日升，洪曉斌

(華南理工大學機械與汽車工程學院，廣東 廣州 510641)

0 引 言

不同于傳統的船模試驗，船舶水動力學 CFD 研究借助計算機的強大功能可提高設計質量，縮短設計周期，降低設計成本，也可為減少船舶阻力、船型優化和改進設計做出指導[1]。李勇躍等[2]運用RANS方程對船舶縱傾進行優化，得出航速和線型會對縱傾優化產生影響的結果。陳一凡[3]對船舶3自由度運動進行了仿真，模擬船舶運動軌跡，并利用Matlab編寫求解程序得出結論文章中的數學模型能夠復現船舶運動。張圣東等[4]基于有限元建立了波浪載荷計算模型和船體變形計算模型，計算得出初相位、浪高和波浪與船的夾角對尾軸載荷的影響。熊楊婷[5]利用CFD對船舶的四種球鼻艏進行了仿真和優化，得出特定條件下的最佳球鼻艏選擇。王易晨[6]運用雷諾平均方法模擬計算復雜船型的船舶阻力進行阻力預報，對比發現RANS方法與試驗值非常接近，可以較為準確的預報船舶阻力。賈寶柱等[7]采用RANS方法的RNGk-ε模型得出了在不同傅汝德數、流攻角、流速變化率和船型下船體周圍流場及壓力場分布。邵峰等[8]采用FLUENT方法來模擬無人船阻力，并進行了試驗驗證。陶毅涵[9]介紹了3種湍流模型：標準k-ε模型、RNGk-ε模型和k-ε、SSTk-ε模型。韓思奇等[10]基于FLUENT研究了雙聲道超聲波流量計聲道，并提出了優化方案。楊劍鋒等[11]面向環境適應性的無人機飛行姿態模擬器進行了設計與仿真。上述這些研究大多采用CFD方法，有些針對大型的傳統運輸船，主要研究了水動力因素對船舶的運動軌跡、縱傾及尾軸載荷的影響，而針對小型無人船水動力學阻力CFD的研究鮮有文獻報道。

本文針對小型無人船水動力學進行CFD模擬，研究吃水深度、航速以及船體偏離水流方向角度條件下的船舶水動力特性。

1 計算模型

1.1 幾何模型

根據早期模型試驗船舶的大小和形狀初步設計無人船船體結構的尺寸：長2m，寬0.6m，高0.33m，如圖1所示。

1.2 計算域與網格模型

1.2.1 計算域

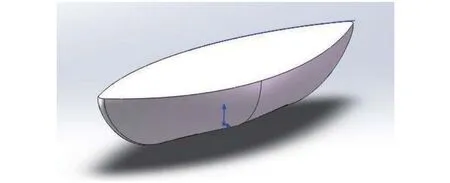
圖1 無人船船體結構

選擇流體域形狀為長方體，以自由水表面為界，流動介質下層為水，上層為空氣，分別設置為速度入口、壓力出口、壁面邊界。即船頭方向為入口inlet，船尾方向為出口outlet，船體和水域底部、船側方向、船上方空氣等邊界的無窮遠處設為壁面wall，確定長方體的計算域，船體前部取1倍船長，船兩側及上下方各取2倍船長，船體尾部取5倍船長。

1.2.2 網格模型

將設置好邊界的計算域導入ICEM-CFD軟件，進行混合網格的劃分，船體表面單元網格大小為64 mm，外部網格為500 mm，網格總數約為30萬，網格質量不低于0.7，如圖2所示。

圖2 網格模型

1.3 數值方法及計算方案

1.3.1 數值方法

設定求解器。選用RNGk-e湍流模型，壓力與速度的耦合方式選擇PISO，進行3次獨立仿真計算。其中，RNGk-e模型方程[12]如式（1）和式（2）所示。

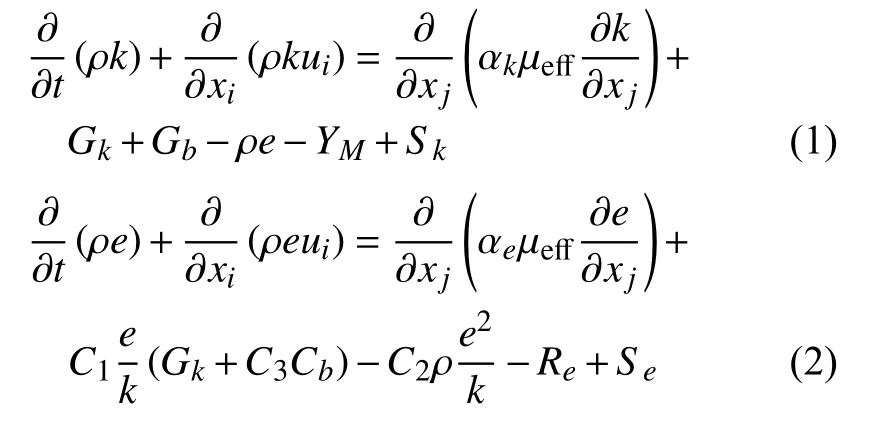
C1，C2，C3——常量；

1.3.2 計算方案

針對小型無人船的試驗研究，一般在水池、人工湖泊、游覽區和江河邊等水流平緩水域，無人船試驗速度相對緩慢。針對不同吃水深度、航速及流速方向確定計算方案如下：

1）航速恒為1 m/s，選取吃水深度分別為4，12，16 cm。

2）吃水深度為 16 cm，選取航速為 0～2 m/s，分別為 0.25，0.5，0.75，1.0，1.25，1.75，2.0 m/s。

3）航速恒為1 m/s，吃水深度為20 cm，水速為1 m/s。航速與水速夾角分別為 0°、15°、30°、45°、60°、75°、90°。

2 無人船水動力特性分析

通過對小型無人船流動特性的模擬，得到無人船航行的速度和壓力，選取一個垂直于船舶航行方向的船中間截面（X=0）的速度和壓力分布，分別從吃水深度、航速、航速與水速夾角這3個方面分析無人船航行阻力特性。

2.1 吃水深度的影響

無人船吃水深度為4，12，16 cm時，垂直于船舶航行方向的船中間截面（X=0）的速度分別如圖3、圖4和圖5所示。

由圖3～圖5可知, 吃水深度分別為4，12，16 cm時, 垂直于船舶航行方向的船中間截面（X=0）上船體周圍的速度范圍分別為 0.9～1.0 m/s、0.7～0.9 m/s、0.4～0.7 m/s，即無人船航行速度隨吃水深度的增大而減小。

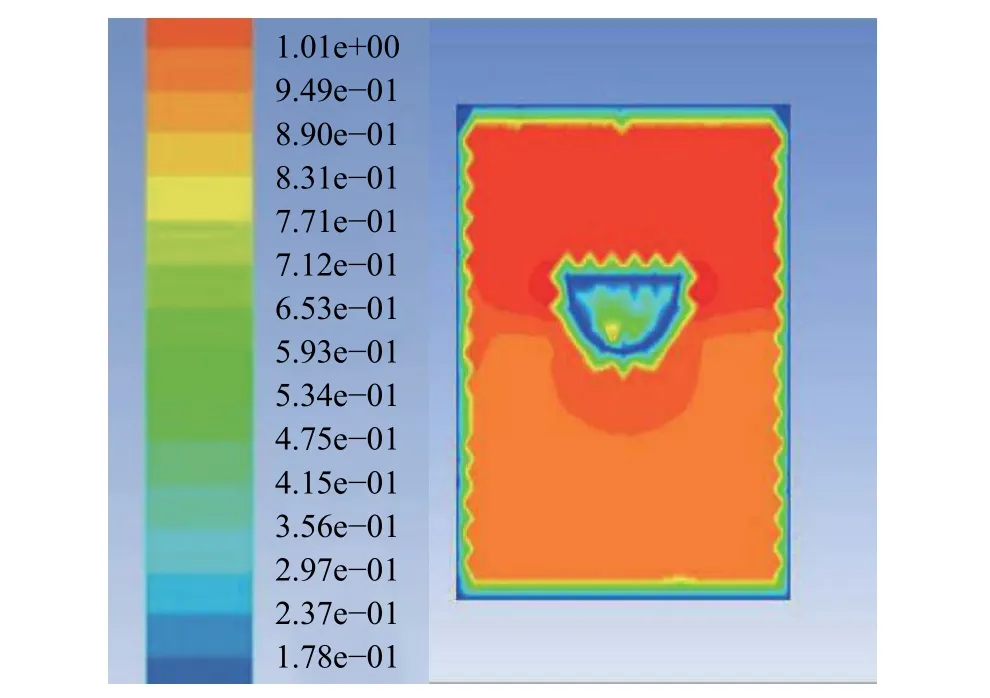
圖3 吃水深度為4 cm時的速度分布

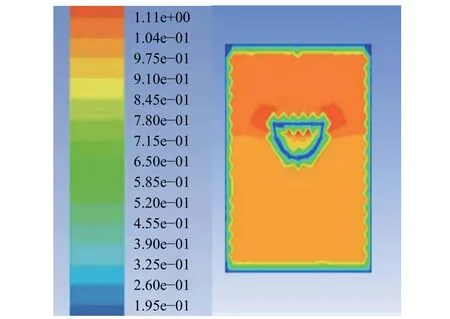
圖4 吃水深度為12 cm時的速度分布

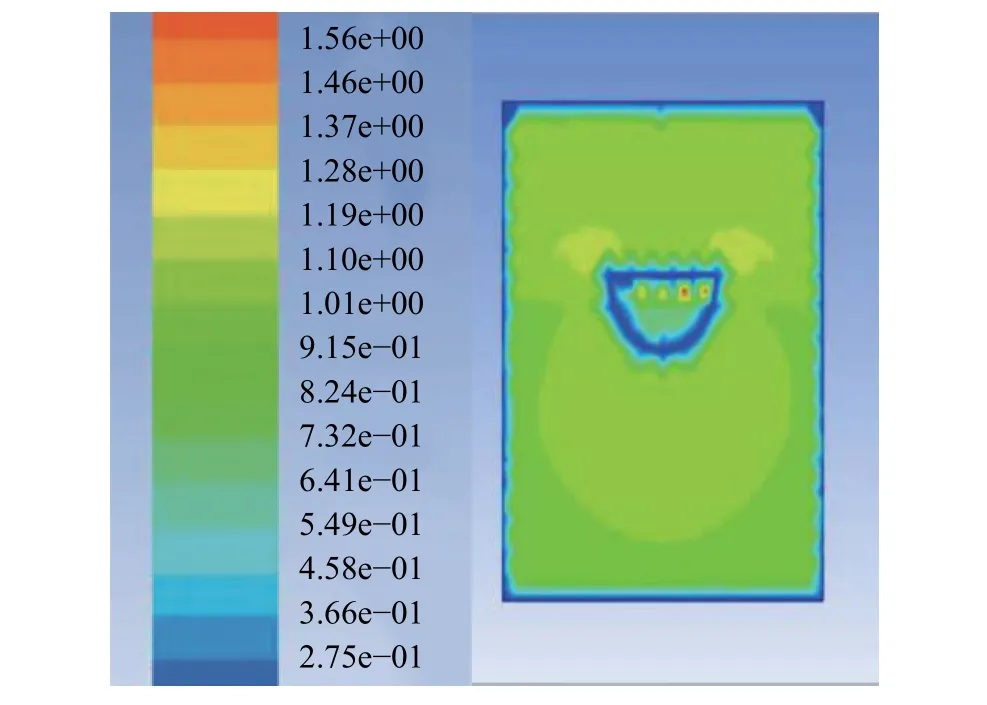
圖5 吃水深度為16 cm時的速度分布

無人船吃水深度為4，12，16 cm時，垂直于船舶航行方向的船中間截面（X=0）的壓力分別如圖6、圖7和圖8所示。

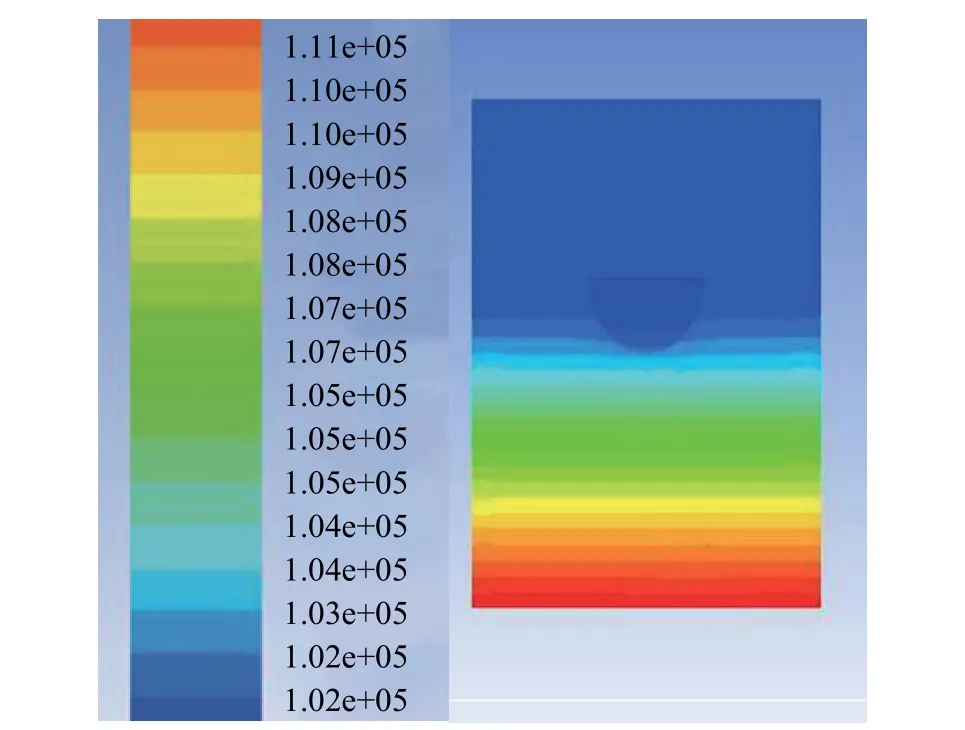
圖6 吃水深度為4 cm時的壓力分布

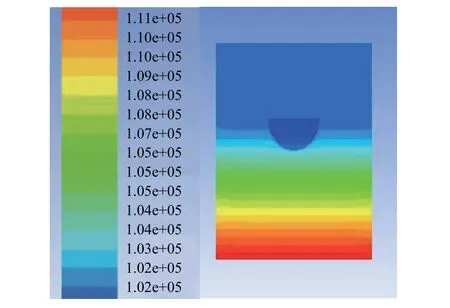
圖7 吃水深度為12 cm時的壓力分布

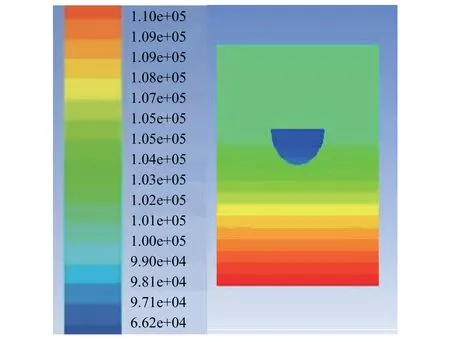
圖8 吃水深度為16 cm時的壓力分布

由圖6～圖8可知，吃水深度分別為4，12，16 cm時, 垂直于船舶航行方向的船中間截面（X=0）上船體周圍的壓力范圍分別為1.01 e+05～1.02 e+05 Pa、1.02 e+05～1.05 e+05 Pa、1.05 e+05～1.08 e+05 Pa，即無人船船體周圍的壓力隨吃水深度的增大而增大。

無人船水動力阻力隨吃水深度的變化如圖9所示。由圖得知，隨吃水深度的增加，無人船船舶阻力逐步增大，且阻力值較小時，波動較小；阻力增大后，波動也隨之增大。

圖9 隨吃水深度變化的船舶阻力

綜上所述，吃水深度從4 cm增加到16 cm時，船舶速度減小，壓力增大；所受到的水動力阻力從0.25 N增加到4.58 N。

2.2 航速的影響

航速分別為0.5，1.25，1.75 m/s時，無人船船體周圍的速度在1.3～1.6 m/s之間,分布無明顯差異，即船舶周圍的水速沒有造成相對明顯的影響。

航速分別為0.5，1.25，1.75 m/s時，無人船船體周圍的壓力在1.03 e+05～1.05 e+05 Pa之間,分布無明顯差異，即船舶周圍的壓力沒有造成相對明顯的影響。

無人船阻力隨航速的變化如圖10所示。由圖可知，隨航速的增大,無人船阻力逐步增大,且航速為0.25～1.25 m/s時，阻力較小且波動不大；1.25～2 m/s時，阻力急劇增大。

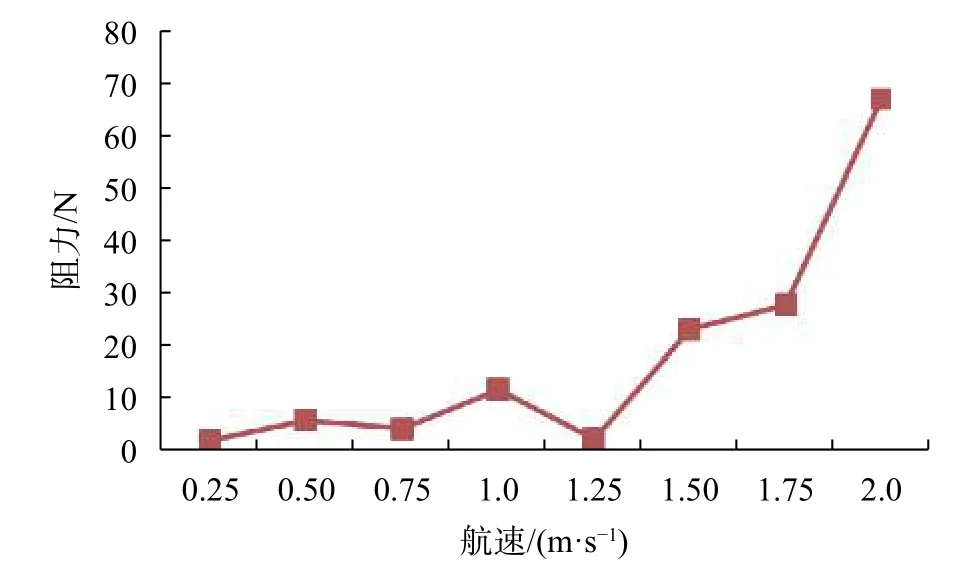
圖10 隨航速變化的船舶阻力

綜上所述，航速在0～2 m/s范圍內逐漸增大時，速度和壓力無明顯變化。航速為0.25～1.25 m/s時，阻力較小且波動不大；1.25～2 m/s時，阻力急劇增大。

2.3 航速與水速夾角的影響

無人船航速與水速夾角分別為 15°、45°、75°時，垂直于船舶航行方向的船中間截面（X=0）的速度分別如圖11、圖12和圖13所示。

由圖11～圖13可以看出，航速與水速夾角為15°時，速度范圍為 1.0～1.3 m/s；45°時，速度范圍為 0.8～1.0 m/s；75°時，速度范圍為 0.4～0.8 m/s。即夾角為15°、45°、75°時，隨著夾角的增大，流速隨夾角的增大而減小。

無人船航速與水速夾角為 30°、45°、60°時，垂直于船舶航行方向的船中間截面（X=0）的壓力分別如圖14、圖15和圖16所示。

圖11 夾角為15°時的速度分布

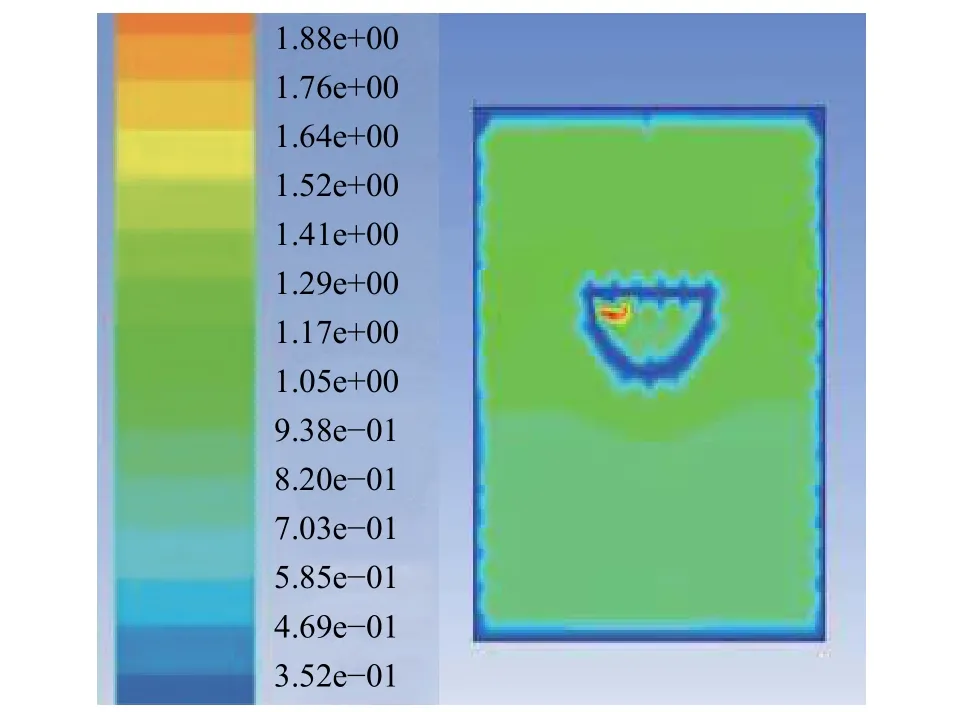
圖12 夾角為45°時的速度分布

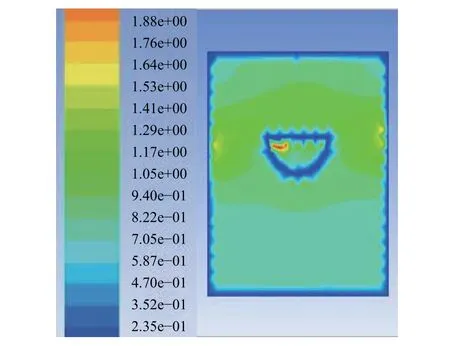
圖13 夾角為75°時的速度分布

由圖14～圖16可以看出，航速與水速夾角為30°時，壓力范圍為 1.05 e+05 Pa～1.08 e+05 Pa；45°時，壓力范圍為 1.08 e+05 Pa～1.11 e+05 Pa；60°時，壓力范圍為 1.01 e+05 Pa～1.05 e+05 Pa。在 0～45°范圍內，壓力隨夾角的增大而增大；在 45°～90°范圍內，壓力隨夾角的增大而減小。

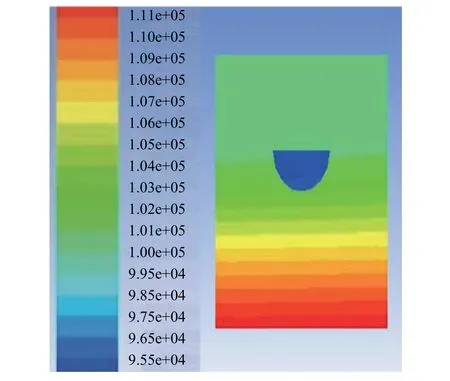
圖14 夾角為30°時的壓力分布

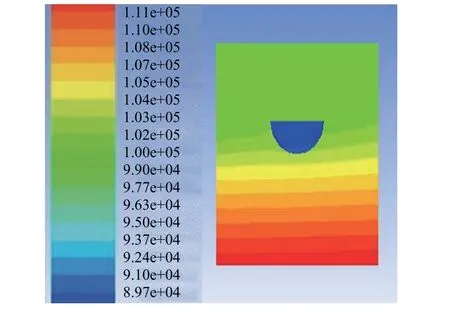
圖15 夾角為45°時的壓力分布

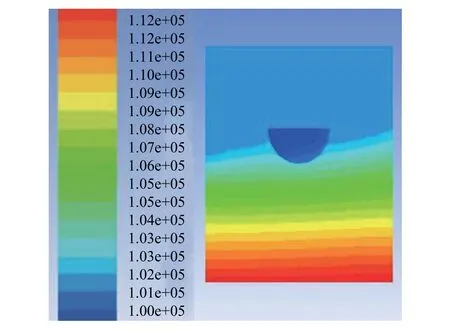
圖16 夾角為60°時的壓力分布

無人船水動力阻力隨航速與水速夾角的變化如圖17所示。由圖可知，無人船水動力阻力隨夾角的增大而明顯增大。

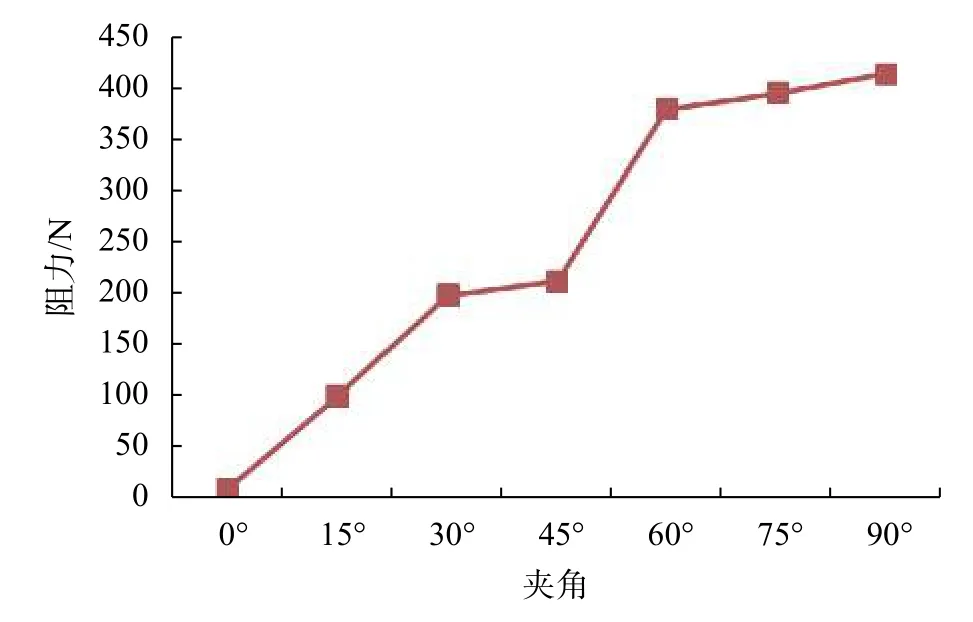
圖17 隨夾角變化的船舶阻力

綜上所述，隨著夾角的增大，速度減小；壓力在0～45°范圍內隨夾角的增大而增大，在 45°～90°范圍內壓力隨夾角的增大而減小；阻力從11.50 N不斷增大到414.71 N。即隨著航速與水速之間的夾角不斷增大，水流作用在船側的橫向作用力越大，阻礙了船舶的正常航行，使得船速逐漸下降。

3 結束語

1) 通過無人船的初步設計，選定計算域與計算方案、劃分網格并建立了無人船水動力CFD模型。

2) 通過對無人船不同吃水深度、航速、航速與水速夾角的CFD模擬表明：吃水深度從4 cm增加到16 cm時，船舶速度減小，壓力增大，所受到的水動力阻力從 0.25 N增加到 4.58 N；航速在 0～2 m/s范圍內逐漸增大時，速度和壓力無明顯變化；航速為0.25～1.25 m/s時，阻力較小且波動不大；1.25～2 m/s時，阻力從2.07 N急劇增加到66.90 N；隨著航速與水速夾角的增大，速度減小，壓力先增大后減小，阻力從11.50 N不斷增大到414.71 N。