電動汽車無線充電系統電磁場計算方法

王林梅，劉 瑞，蔣佐富，陳 鑫，周仲岳，張克涵

（1.臺州宏遠電力設計院，浙江 臺州 318000；2.國網浙江省電力有限公司臺州供電公司，浙江 臺州 318000；3.西北工業大學，西安 710072）

0 引言

當前我國電動汽車產業已步入快速發展期，充電設施建設如火如荼[1]。電動汽車的無線充電技術可以解決火花、積塵、接觸損耗及機械磨損等一系列傳統充電方式所帶來的問題，提高電動汽車的續航能力[2]，因此電動汽車無線充電將成為未來主要的發展方向。

目前，無線電能傳輸技術主要有3種方式：基于磁耦合的IPT（感應電能傳輸）、基于電場耦合的CPT（電容能量傳輸）、微波輻射。基于磁耦合諧振的非接觸式電能傳輸系統，在傳輸距離較遠時也可以實現大功率高效電能傳輸；基于電場耦合的無線電能傳輸系統，結構簡單，制造成本低，具有很大的發展空間[3]；基于微波輻射的傳輸方式，其傳輸距離遠遠大于傳輸裝置的幾何尺寸[4]，其缺點是傳輸效率較低。CPT及IPT技術均可應用到電動汽車無線充電系統中。IPT作為一種傳統無線電能傳輸技術，原理簡單，容易實現，因此在電動汽車無線充電領域具有廣闊的應用空間。目前國內外在磁耦合無線電能傳輸方面的研究主要集中在阻抗匹配、系統動態控制、電磁兼容及生物安全問題等方面[5]。磁耦合諧振式WPT（無線電能傳輸）技術起步較晚，但近年來受到了較多的關注[6]。

1 IPT研究國內外現狀

2007年，MIT（麻省理工）的科學家首先基于耦合模理論對磁耦合諧振WPT進行系統建模，分析傳輸距離、工作頻率、天線結構參數對傳輸功率和傳輸效率的影響，然后分析耦合諧振的非輻射能量傳輸特性[7-8]，為提高傳輸效率和增大傳輸距離，先后提出了2種改進的諧振器結構，即中繼諧振器結構和多接收負載諧振器結構[9-10]。日本東京大學 Takehiro等通過等效電路和紐曼公式[11]，實現傳輸效率的最優化。2008年，Intel公司的J.R.Smith展示了基于磁耦合諧振技術的研究成果，在演示過程中，該系統以75%的效率實現了60 W傳輸功率[12]。華南理工大學張波教授課題組從電路角度分析系統傳輸效率與線圈尺寸、距離等之間的關系，從而進行無線電能傳輸系統優化設計[13]。東南大學將無線傳輸的距離增加到50 cm左右，傳輸功率大于1 kW[14]。

目前對于IPT系統，多采用互感模型進行分析，這種分析方法只能定量地表示出次級線圈感應電壓和感應電流，進而得出輸出功率，但這種方法并不能分析系統參數對系統性能的影響，無法具體分析系統傳輸機理，難以對系統耦合線圈進行優化設計。因此本文采用電磁場分析方法，首先利用電磁場的矢量疊加原理，推導得出多匝線圈產生的電磁場解析表達式，從而得出WPT系統初、次級側線圈產生的合成電磁場解析表達式，并應用COSMOL仿真軟件和WPT實驗系統，驗證了電磁場解析表達式的正確性，對WPT系統的傳輸機理進行了深入研究。

2 IPT基本原理

應用磁耦合諧振IPT技術對電動汽車進行無線充電，其基本原理為：汽車停車位下面的初級側線圈產生交變電磁場，在汽車底盤安裝的次級側線圈感應出交變電流，經過AC/DC（交流/直流）以及DC/DC（直流/直流）變換，轉換為滿足電池充電要求的直流電，電路模型如圖1所示。

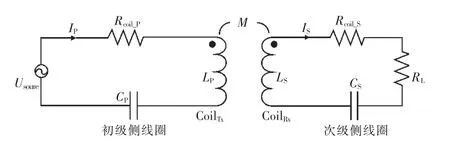
圖1 串串型電路模型

其中，LP和LS分別為初級側、次級側線圈自感；M為兩線圈之間的互感；CP和CS分別為初級側、次級側補償電容；Rcoil_P和Rcoil_S分別為初級側及次級側線圈交流阻抗；RL為負載阻抗；Usource為電源。在初級側、次級側均達到諧振狀態時，傳輸效率η和功率PL表示如下：

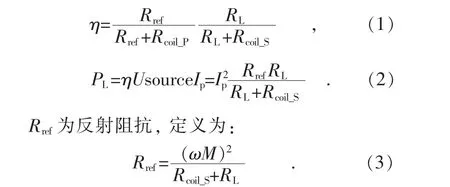
3 電磁場計算

一般而言，線圈采用的結構可分為螺旋線圈結構和平面線圈結構，多匝線圈的結構如圖2所示，線圈半徑為a。

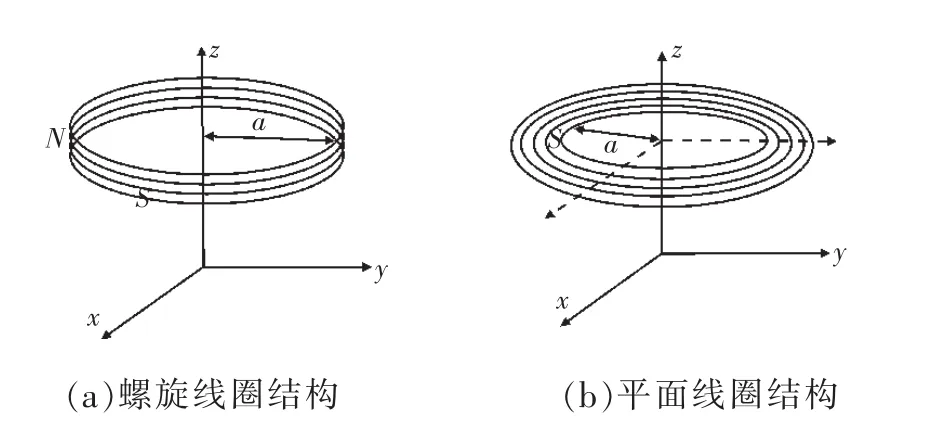
圖2 多匝線圈結構

空間中平面線圈和螺旋線圈是軸對稱的，其產生的電磁場在空間中也具有對稱性，可以由單匝線圈產生的電磁場的解析表達式，來研究多匝線圈在空間產生的電磁場分布狀況。因螺旋線圈與平面線圈解析表達式的推導方式基本相同，本文僅推導螺旋線圈在空間中產生電磁場的解析表達式，然后建立相應的仿真模型，搭建實驗系統，驗證解析表達式的正確性。

3.1 單匝線圈

如圖3所示，選螺旋線圈中軸線與z軸重合，t=0時刻初級側線圈電流方向和軸正向呈右手螺旋關系O-ρφz，建立線圈柱面坐標系，電流的時域表達式為 i（t）=Icos（ωt）。假設通電線圈處于線性均勻的無限介質中，ε，μ，σ分別表示介質的介電常數、磁導率和電導率[15]。

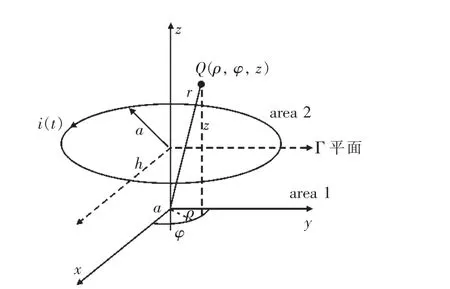
圖3 單匝通電線圈柱面坐標系

圖3中線圈半徑為a；r表示原點O與任意點 Q（ρ，φ，z）的間距。通電線圈處于 Γ（z=h）平面上， 規定 z＜h區域為 area 1，z＞h區域為 area 2，即在area 1和2內沒有電流源的分布，電流源僅分布在area 1和2的邊界處。

空間中任意一點 Q（ρ， φ， z）處電場強度 E（ρ，φ，z）為[16]：

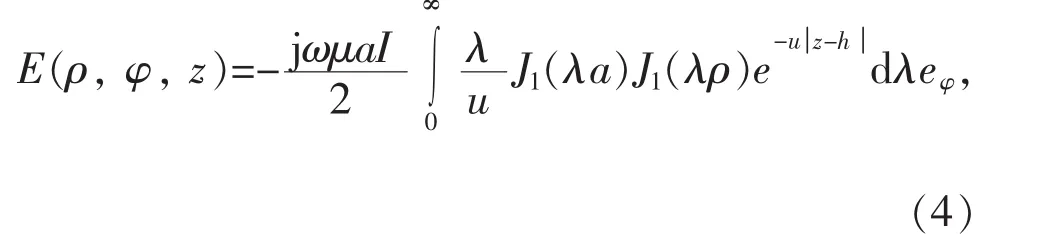
由電場強度E和磁場強度H的關系，可得Q（ρ， φ， z）處磁場強度 H（ρ， φ， z）為：

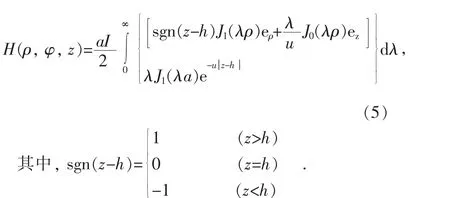
3.2 N匝螺旋線圈電磁場計算

N匝螺旋線圈可以看作圖4中灰色單匝線圈沿z軸方向平移（N-1）次得到，單次平移間距為s，螺旋線圈可以分解成N個單匝線圈。N和a分別表示通電線圈的匝數以及半徑，Q（ρ，φ，z）表示柱面坐標系中任意一點，r表示坐標原點O到Q點的距離。根據單匝線圈產生的電場強度公式（4），可以推導出灰色單匝線圈沿z軸平移（N-1）s之后，在Q（ρ，φ，z）處產生的電磁場解析表達式，將多匝線圈產生的電場強度和磁場強度做矢量疊加，可以得到N匝螺旋線圈在Q（ρ，φ，z）產生的電場強度 E（ρ， φ， z）和磁場強度 H（ρ， φ， z）解析表達式為：

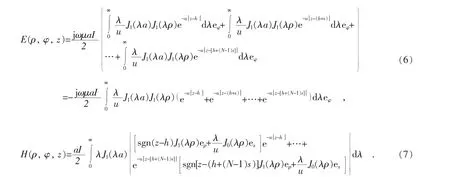
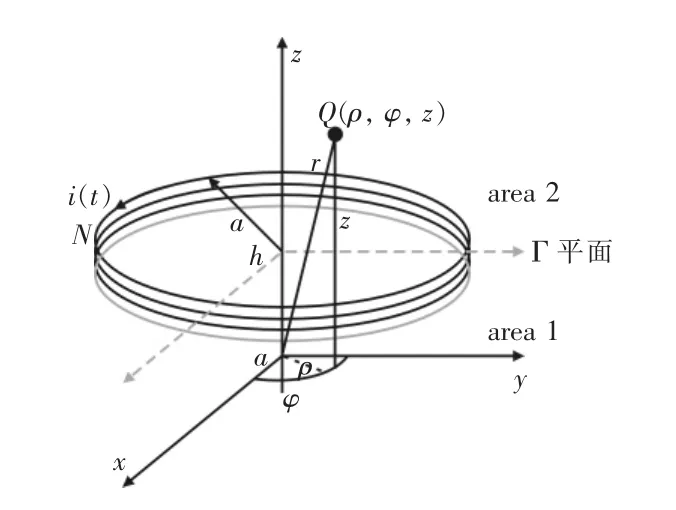
圖4 螺旋線圈柱面坐標系

3.3 WPT系統電磁場計算

在空間中的電場和磁場是初、次級側線圈產生的電場和磁場的矢量疊加，建立螺旋線圈柱面坐標系如圖5所示，Nj和aj分別表示線圈匝數和內半徑，hj表示線圈平面與z=0的xoy平面的垂直距離，Q（ρ，φ，z）為任意一點，rj是坐標原點O到Q點的距離，其中j=p時表示初級側線圈的參數，j=s時表示次級側線圈的參數。

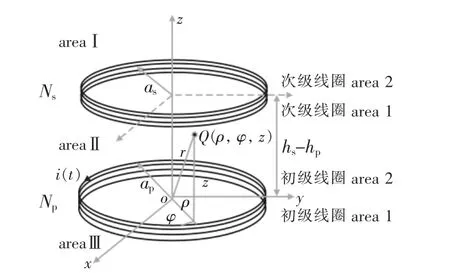
圖5 螺旋線圈結構初、次級側線圈柱面坐標系

當位于多匝線圈的單側時，式（6）、式（7）可化簡為式（8）、 式（9）：

空間中電場強度Etotal和磁場強度Htotal是初級線圈產生的Ep，Hp和次級側線圈產生的矢量和，由式（8）、式（9）可得到在areaⅡ區域電磁場解析表達式（10）、 式（11）：

4 仿真驗證

采用有限元分析軟件COMSOL搭建仿真系統，對螺旋線圈構成的WPT系統電磁場解析式進行仿真分析，驗證解析表達式的正確性。根據上節推導可知，電場強度和磁場強度與φ無關，選取φ=0截面進行仿真分析。

4.1 電場強度

取φ=0截面中任意一條直線上的E解析值與仿真值進行比較，線圈參數如表1所示。取φ=0，ρ=60 mm，10 mm≤z≤60 mm， 利用 COMSOL進行仿真，再使用式（6）計算出解析值，作出電場強度幅值和相位圖，如圖6和圖7所示。

表1 螺旋線圈參數

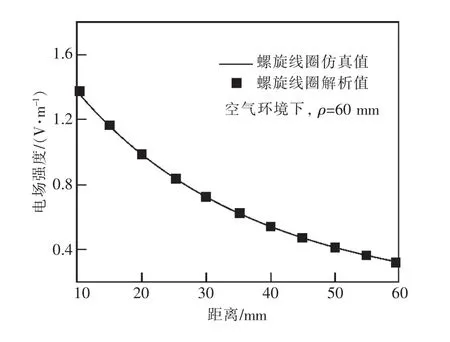
圖6 電場強度幅值

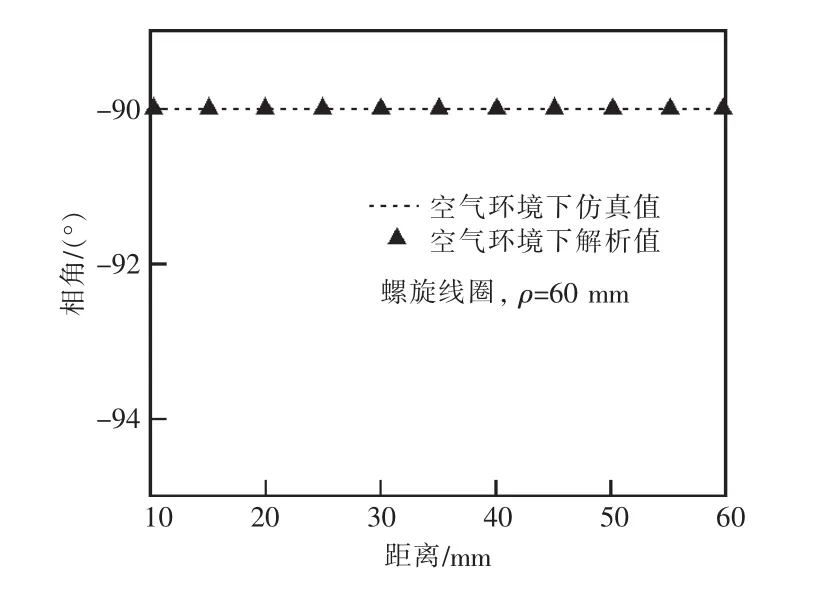
圖7 電場強度相角

從圖6和圖7可以看出，電場強度的幅值和相角的解析值以及仿真值非常接近，從而驗證了螺旋線圈電場強度E解析式的正確性。

4.2 磁場強度

為了驗證磁場強度的解析式，令ρ=60 mm，z從10mm到60 mm變化，利用COMSOL計算出螺旋線圈產生的磁場強度仿真值，參數如表1所示，利用式（7）得出磁場強度解析值，其對比如圖8所示。

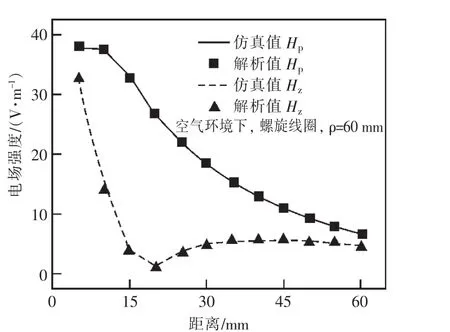
圖8 空氣中螺旋線圈產生的磁場強度對比

H在空間中只有ρ和z方向上的分量。根據圖8可知，仿真值和對應的解析值吻合很好，說明螺旋線圈在空間任意一點產生的磁場強度解析式是正確的。

5 實驗驗證

通電線圈在空間中產生交變電磁場，線圈在交變電磁場中感應出的電壓Uopen是線圈所在處E的環路積分，表達式為：

利用示波器的電壓鉗測量感應線圈電壓值，利用有限元分析軟件建立線圈模型，得出感應電壓仿真值，通過式（12）算出感應電壓解析值，比較實驗值、仿真值以及解析值，驗證式（10）電磁場解析表達式的正確性。

5.1 單線圈電場試驗驗證

初級側線圈通入正弦交變電壓，次級側線圈保持開路，保持初級側電路電流為1.5 A，同時改變電流頻率，使用示波器測量次級側開路線圈感應電壓，電路拓撲結構如圖9所示，線圈參數如表2所示。作出感應電壓Uopen實驗值、仿真值及解析值的對比曲線，如圖10所示。

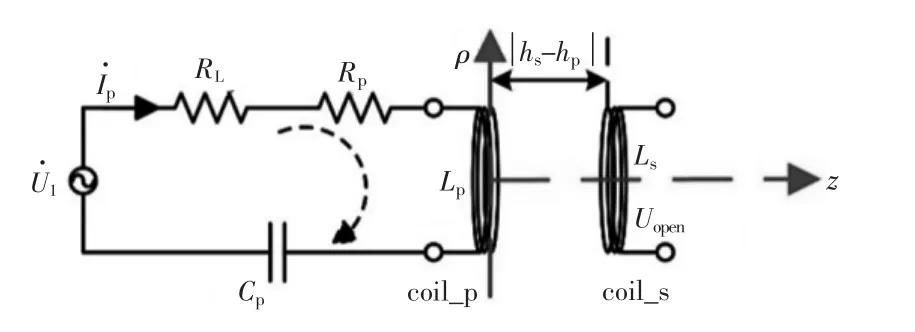
圖9 單線圈通電電磁場驗證拓撲結構

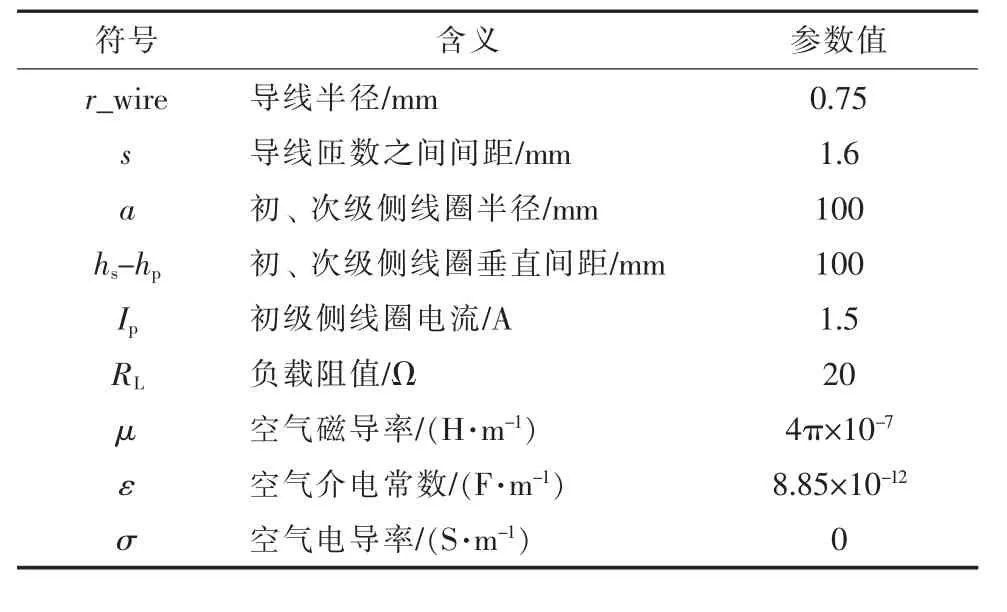
表2 通電線圈參數

對圖10分析可知，五角星（★）對應的是解析值，空心圓（○）代表的是實驗測量值，而直線或者虛線代表仿真值，對應著不同線圈的匝數。解析值、測量值及仿真值均非常接近，驗證了式（8）螺旋線圈電場強度解析式的正確性。

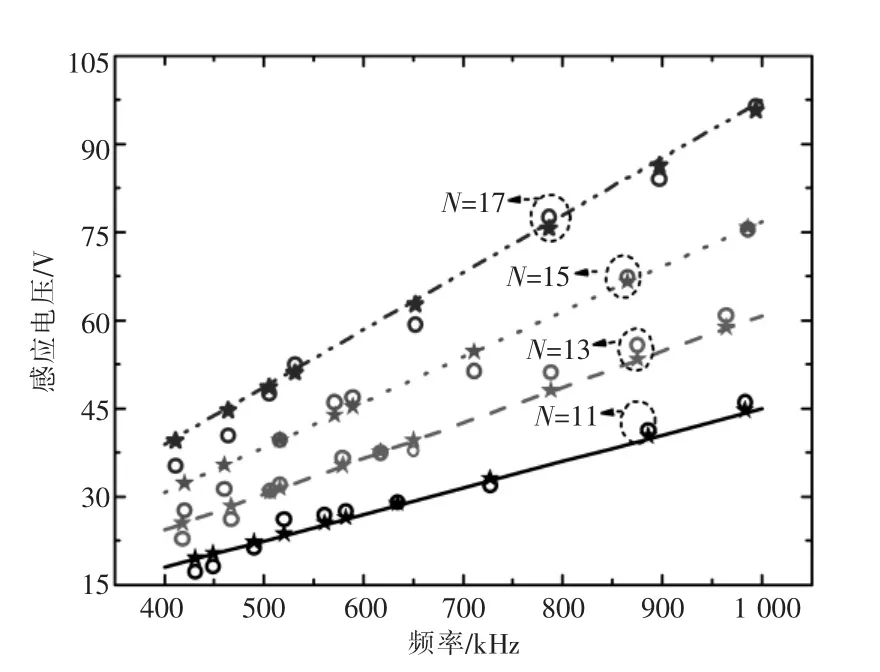
圖10 開路線圈感應電壓

從圖10可以明顯看到，匝數越大，次級側線圈感應電壓Uopen越大，一方面是因為初級側線圈匝數越大，在電流一定的情況下，產生的電場強度越強；另一方面次級側線圈匝數變多，從而感應電壓相應增加。匝數固定時，次級側線圈感應電壓Uopen隨頻率的增大而增大。感應電壓的變化規律與電場強度解析表達式相符合。

5.2 WPT系統電場試驗驗證

當初級側線圈通入正弦交變電壓后，在空間中會產生交變電場Ep，當次級側線圈回路接通，形成電流回路，在空間中產生另一個交變電場Es，與Ep矢量疊加，從而形成新的電場Etotal。在初、次級側線圈中間放置一個同軸開路單匝線圈，線圈感應電壓U的解析式為：

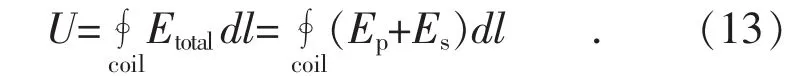
實驗系統拓撲如圖11所示，線圈參數如表3所示，當初級側線圈電流頻率為500 kHz時，對單匝線圈進行平移，測量不同位置的感應電壓，同時作出感應電壓變化曲線，如圖12所示。

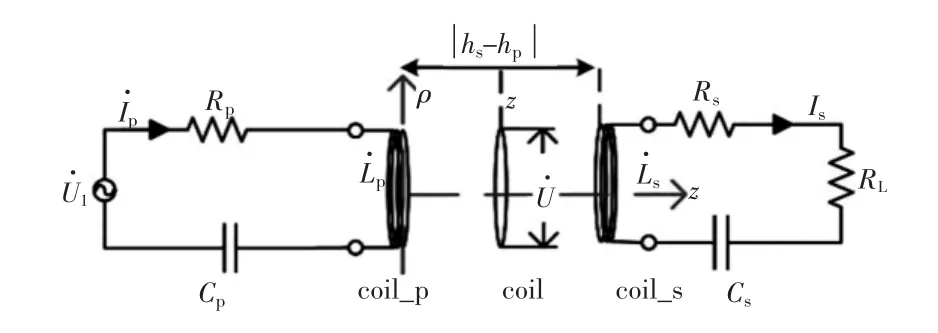
圖11 WPT系統拓撲

表3 通電線圈參數

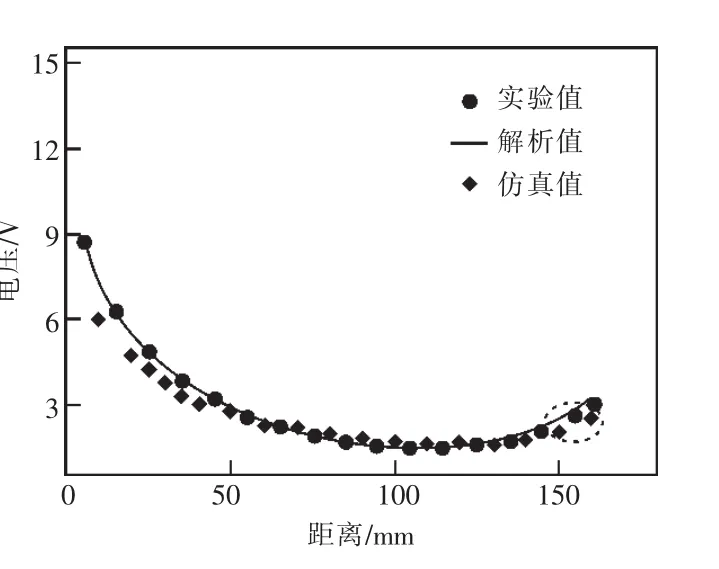
圖12 線圈感應電壓

從圖12可以看出當匝數和頻率固定時，初級側線圈和次級側線圈之間隨著單匝線圈位置的改變，由初級側線圈和次級側線圈分別產生的交變電場隨之改變，經過電場疊加，單匝線圈感應電壓發生變化。圓點（●）和菱形（◆）分別代表實驗值和仿真值，直線代表解析值，相同參數下實驗值、解析值以及仿真值互相吻合，證明了式（13）的正確性，從而證實了系統電場強度解析表達式（10）的正確性。由于電場強度與磁場強度有固定的約束關系，也間接說明磁場強度的解析表達式（11）是正確的。

6 結語

本文首先利用電磁場的矢量疊加原理，推導得出多匝線圈產生的電磁場解析表達式，從而得出WPT系統初、次級側線圈產生的合成電磁場解析表達式。隨后應用CPOSMOL仿真軟件，進行了仿真分析，仿真值和對應的解析值吻合很好，說明電磁場解析表達式的正確性。最后搭建WPT實驗系統，進行實驗驗證，證明了提出的電磁場分析方法的正確性，為相關系統參數優化提供了參考。