柵格翼在減小火箭殘骸落點散布上的應用

賈洪印 徐明興 張培紅 吳曉軍 和爭春

?

柵格翼在減小火箭殘骸落點散布上的應用

賈洪印 徐明興 張培紅 吳曉軍 和爭春

（中國空氣動力研究與發展中心計算空氣動力研究所，綿陽 621000）

文章利用柵格翼高氣動效率、高阻力的特點，探索其在火箭芯一級殘骸落點散布控制上的應用。首先介紹了柵格翼氣動性能分析采用的數值模擬方法，通過與試驗數據對比，驗證了方法的可靠性。針對火箭芯一級箭體，開展了柵格翼設計研究，給出了詳細的柵格翼幾何尺寸，分析了其在亞跨超聲速階段氣動性能，通過6自由度蒙特卡羅彈道拉偏仿真，對比了柵格翼安裝前后火箭芯一級殘骸落點散布范圍。結果表明，火箭芯一級加裝柵格翼后，上升段折疊安裝，阻力增量較小，超聲速階段阻力增量2%以內；再入段柵格翼打開，小迎角范圍內火箭芯一級殘骸壓心后移明顯，氣動穩定性增強；芯一級殘骸進入大氣層后飛行姿態迅速振蕩收斂，殘骸落點散布范圍大幅縮小，安裝柵格翼后火箭芯一級落點散布面積減小約76%，這種基于穩定柵格翼進行落點控制的方法具有機械結構簡單，易于工程實現的特點，適用于各類運載火箭的改造，可大幅度減小落區的范圍。

柵格翼 穩定性 落點散布 彈道仿真 火箭 航天回收

0 引言

失穩飛行器，如：飛行器破損產生的殘骸、火箭脫落的整流罩和助推級等，通常是不可控的飛行器，墜落到地面時有可能帶來安全問題[1]。為了保障這些飛行器的落區安全，可以從兩個方面入手[2]：一是將其落點控制在人煙稀少的地方；二是提高落區劃定的精度，減小落點散布的范圍。由于受到飛行器目標軌道、發射場位置、機動能力、總體設計等方面的限制，這些失穩飛行器的落點難以有效控制到人煙稀少的地方，因此提高落區劃定的精度，減小落點散布的范圍，對保障落區人員和財產安全，具有十分重要的意義。

運載火箭子級按回收的方式不同，大致可分為傘降回收、帶翼飛回式和垂直返回回收三種類型[3]。傘降回收[4]是利用降落傘實現火箭子級的減速過程，通過姿控發動機（Reaction Control System，RCS）或者翼傘來調整姿態，實現火箭子級的回收。美國在傘降方面積累了大量經驗，發展了用于航天飛機固體火箭助推器回收系統[5]。傘降回收的典型代表是美國的航天飛機助推器、戰神I-X助推器[6]、K-1運載火箭[7]等。帶翼飛回式子級回收的主要思想是在傳統火箭上添加機翼，利用控制舵面和RCS系統，實現水平著陸，如美國的航天飛機、俄羅斯正在研制的新型運載火箭“安哥拉”[8]。火箭子級垂直回收是火箭子級在完成任務后，通過自身攜帶的控制系統和動力裝置，按照設定的軌跡自主飛回著陸場，并以垂直的箭體姿態緩慢降落到指定著陸場，其典型代表就是美國Space X公司的Falcon 9火箭[9]和藍色起源公司的New Shepard火箭。相比有翼水平著陸的子級回收方式，垂直返回對火箭外形及總體布局影響較小。在火箭子級垂直返回回收中，涉及多項復雜關鍵技術[10]，如再入大氣層熱防護技術、先進火箭發動機技術、垂直返回高精度控制技術、高可靠性著陸支撐技術等。Space X公司在Falcon 9火箭垂直返回控制中，采用了柵格舵和RCS復合的再入返回控制方案，實現了助推火箭一子級的精確回收。

柵格翼是一種新型控制穩定面，由多個薄的柵格壁板構成。它作為一種新型升力面和控制面，在亞聲速和高超聲速階段有比平板翼更優秀的氣動特性，可用作穩定翼或全動式舵翼以提高彈箭的機動性，增加其穩定性和可控性[11]。與傳統平板翼相比，柵格翼具有一些獨特優點[12-15]，在相同的外形尺寸下，柵格翼的升力面積比平板翼大得多；具有較高的強度質量比；柵格翼弦向尺寸小，可以緊貼主體折疊安裝，而不增加主體的外形尺寸；在控制效率和鉸鏈力矩特性方面優于傳統平板翼。對于炸彈和導彈等飛行器，柵格翼缺點主要是相較于平板翼阻力較大，而對于高速返回的火箭芯一級箭體，這個缺點卻成為了優點，可以提供額外的氣動阻力，減小火箭芯一級殘骸返回速度。

本文借鑒Space-X火箭回收技術，利用柵格翼高氣動效率、高阻力的特點，探索柵格翼在火箭芯一級殘骸落點散布控制上的應用。本文首先介紹了柵格翼氣動性能分析采用的數值模擬方法，通過與試驗數據對比，驗證了方法的可靠性。針對火箭芯一級箭體，開展了柵格翼設計研究，分析了其在亞跨超聲速階段氣動性能，通過6自由度蒙特卡羅彈道拉偏仿真，對比了火箭芯一級殘骸安裝柵格翼前后飛行姿態變化和落點散布范圍的變化。

1 數值分析方法及驗證

1.1 數值模擬方法介紹

本文柵格翼氣動特性數值模擬分析采用中國空氣動力研究與發展中心自主研制的亞跨超聲速流場解算器MFlow，該解算器支持任意形狀的網格單元，具備大規模并行能力，可用于各種定常、非定常流動問題的模擬，在航空航天領域得到了廣泛的應用，軟件經過了大量標準算例的考核驗證[16-18]。

在本文的研究中，控制方程采用三維非定常可壓縮的Navier-Stokes方程，計算網格采用三棱柱和四面體混合的非結構網格單元，主控方程對流項采用目前應用廣泛、具有較高間斷和黏性分辨率的Roe格式進行離散，黏性項采用中心格式，時間推進采用隱式LU-SGS（Lower Upper Symmetric Gauss-Seidel）方法，線性重構時梯度求解采用節點型Gauss方法。為了加速流場收斂，采用了局部時間步長和FAS（Full Approximation Storage）融合的多重網格技術。在湍流流動模擬方法方面，采用目前工程應用廣泛、魯棒性高的SA（Spalart Allmaras）一方程湍流模型。物面采用無滑移、無穿透、絕熱邊界條件，遠場采用無反射遠場邊界條件。

1.2 方法驗證

在跨聲速階段，柵格翼內存在流動壅塞現象[19]，對數值模擬要求較高，為了驗證本文數值模擬方法和網格技術的可靠性，以某導彈為研究對象，選取其2×4柵格翼導彈標模外形，對數值模擬方法進行了驗證確認。帶柵格翼的導彈外形及尺寸如圖1（a）所示，柵格翼詳細尺寸及三維幾何外形如圖1（b）所示，圖中尺寸以彈體底部直徑進行了歸一化，為頭部曲線對應的圓弧半徑。數值模擬采用三棱柱和四面體混合的非結構網格單元，如圖2所示，網格總量約為1 500萬個，網格第一層間距歸一化≈1，在前緣和柵格翼表面等區域，采用各向異性網格技術，柵格翼弦向網格點數35個，格子寬度方向網格點數25個。

圖3給出了跨聲速階段馬赫數為0.8~1.6范圍內全彈零升阻力計算、風洞試驗結果[20]和文獻參考值[21]的對比曲線。可以看出，數值計算結果與風洞試驗結果吻合較好，說明采用的數值計算方法可以較好地預測柵格翼跨聲速階段復雜的流動特性，驗證了本文柵格翼氣動特性分析方法的可靠性。

圖1 柵格翼標模尺寸

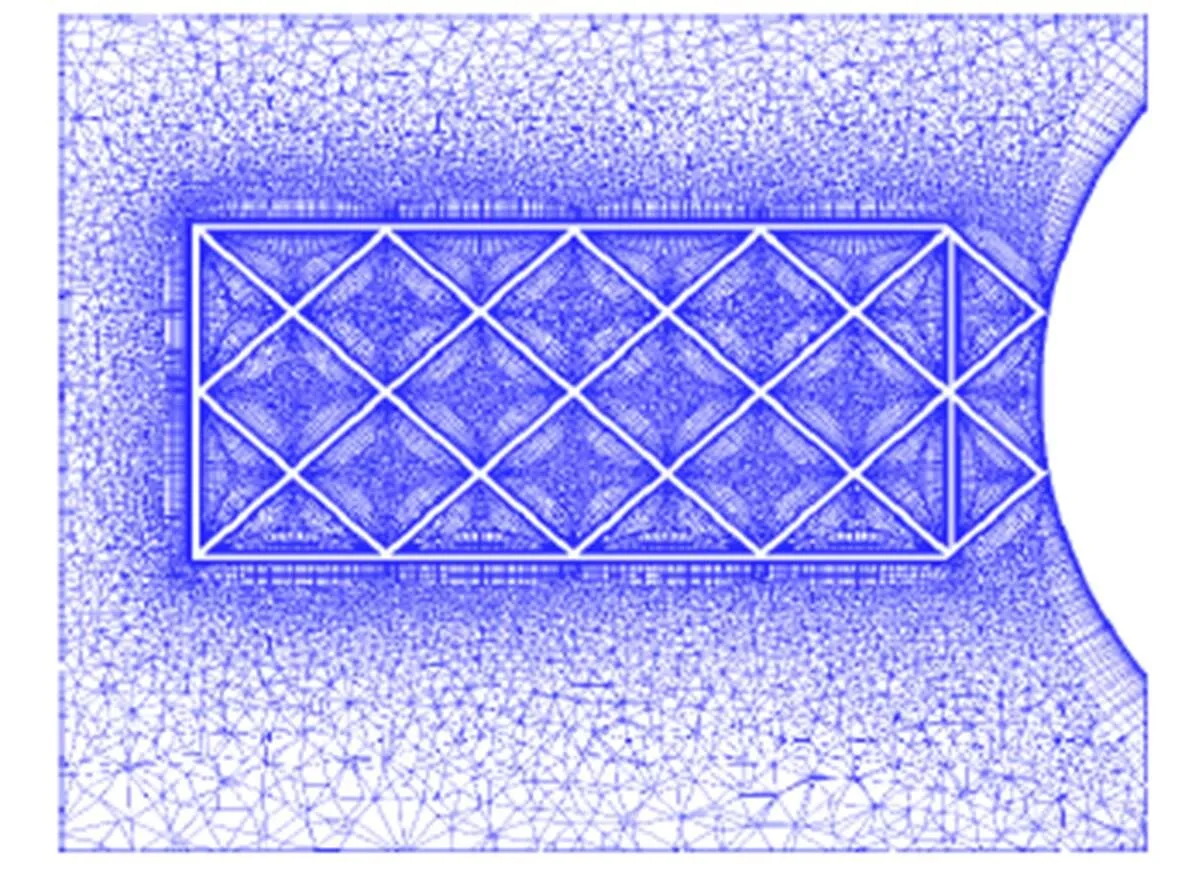
圖2 柵格翼截面網格

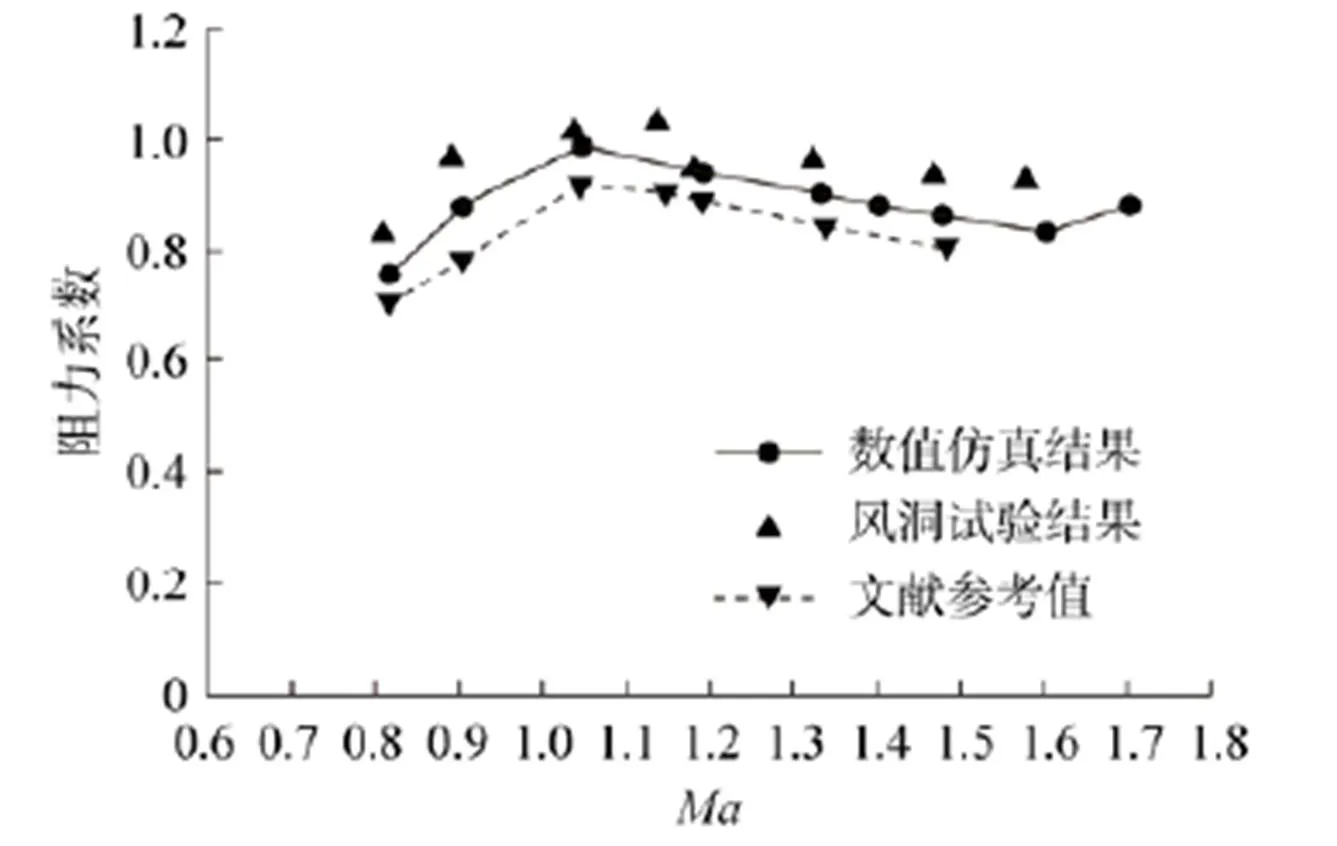
圖3 計算與風洞試驗對比

2 柵格翼設計及氣動性能分析

2.1 柵格翼設計

針對火箭芯一級箭體，開展了柵格翼設計研究，具體設計要求如下：在結構方面，為了減小安裝柵格翼對火箭運載能力的影響，要求設計的柵格翼在上升段可折疊安裝在火箭芯一級箭體上，柵格翼結構質量盡可能小，結構強度滿足全速域使用要求；在氣動性能方面，要求上升段對火箭自身氣動性能影響較小，高速返回段柵格翼展開后滿足氣動穩定性要求。

圖4給出了設計的柵格翼外形圖，柵格翼采用弧形設計，上升段可折疊安裝在箭體上，格子數目為6×7，柵格翼外邊框尺寸為1 416mm×1 208mm，柵格翼弦長100mm，格寬135mm，格弦比為0.74，格壁厚度為5mm，外框厚度10mm。同時，為了滿足折疊安裝要求，設計了相應的折疊和轉動機構。假設柵格翼材質為實心全鋼結構，單片柵格翼的總質量約為150kg。由于本文設計的柵格翼不需要考慮減阻特性，所以柵格翼前緣位置并未倒圓處理。

2.2 氣動性能分析

針對設計的柵格翼外形，將其安裝在火箭芯一級箭體上，開展了上升段和返回段氣動特性數值仿真分析。四片柵格翼呈“X”形布局形式，安裝在火箭一、二級連接艙位置，柵格翼展開后的外形如圖5所示。

數值模擬采用三棱柱和四面體混合的非結構網格單元，網格總量約為6 800萬個，其中三棱柱單元約為4 800萬個，四面體單元約為2 000萬個，網格第一層間距≈1。圖6給出了模擬采用的表面網格和空間網格分布圖，可以看出，在柵格翼的表面，采用了各向異性的三角形單元進行模擬，柵格翼弦向網格點數為24個，格子寬度方向網格點數為20個，為了較好的模擬黏性效應，附面層內采用棱柱層進行模擬。同時，在柵格翼附近整個空間區域都進行了加密處理，可以滿足柵格翼氣動力數值模擬要求。

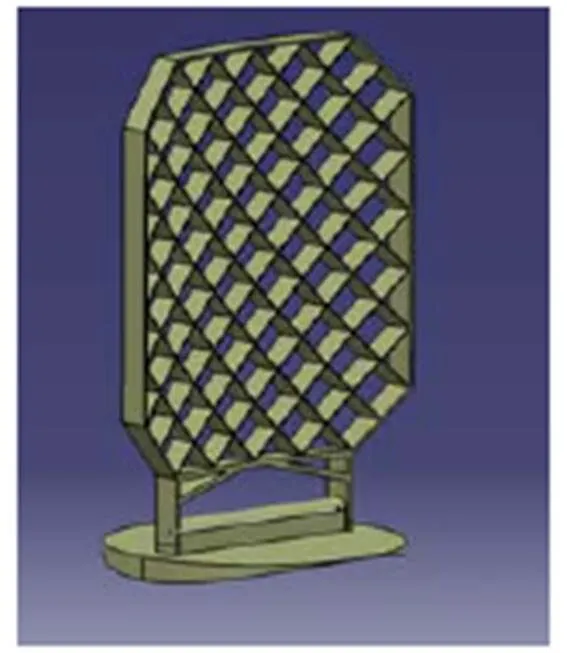
圖4 設計的柵格翼外形

圖5 火箭芯一級加裝柵格翼外形

氣動特性數據分析基于英美坐標系，即軸向前為正，軸向右為正，軸向下為正，參考質心距離火箭底部32%總長度，柵格翼質量相對火箭箭體質量為小量，忽略安裝柵格翼對火箭殘骸質心的影響。

在上升段，柵格翼折疊安裝在火箭箭體上，需要評估增加柵格翼后對火箭上升段氣動特性的影響。圖7給出了上升段柵格翼折疊后對整個火箭阻力特性的影響曲線，可以看出，柵格翼折疊后對火箭上升段的阻力影響較小，在超聲速階段，火箭阻力增量在2%以內，亞聲速時由于火箭總阻力相對較小，阻力增量的百分比略有增大，但最大不超過總阻力的6%。

在再入段，火箭芯一級殘骸屬于無控飛行器，其飛行迎角、姿態主要由芯一級箭體的氣動穩定性決定。圖8給出了亞、跨、超聲速典型馬赫數下0°～180°迎角范圍內有無柵格翼火箭芯一級殘骸俯仰力矩特性和壓心特性的對比曲線。圖中俯仰力矩特性曲線力矩參考點為火箭芯一級殘骸質心，表示馬赫數。可以看出，火箭芯一級殘骸增加柵格翼后，在小迎角范圍內，壓心發生明顯的后移，隨著迎角的逐漸增大，柵格翼面開始發生流動分離，柵格翼的氣動效率降低，壓心后移量逐漸減小；在120°迎角以后，由于氣流方向的改變，柵格翼的氣動效率開始逐漸增強，壓心后移量隨著迎角的增大而逐漸變大。同時，從俯仰力矩特性曲線可以看出，有無柵格翼外形俯仰力矩隨迎角變化的趨勢基本一致，其原因是在較大迎角時，柵格翼上產生的俯仰力矩比箭體產生的俯仰力矩小很多，俯仰力矩變化主要由箭體上俯仰力矩變化產生。在小迎角時，箭體自身產生的俯仰力矩量值和柵格翼上的俯仰力矩量值基本相當，從而使得小迎角范圍內的穩定性發生了改變。對比不同馬赫數下的俯仰力矩特性曲線，可以看出，對于無柵格翼外形，在0°~180°范圍內，存在多個俯仰力矩系數為零的平衡點，增加柵格翼后，平衡點個數減小為2個，對應迎角分別為0°和180°，且180°迎角時，俯仰力矩對迎角的導數大于0，為靜不穩定平衡點。

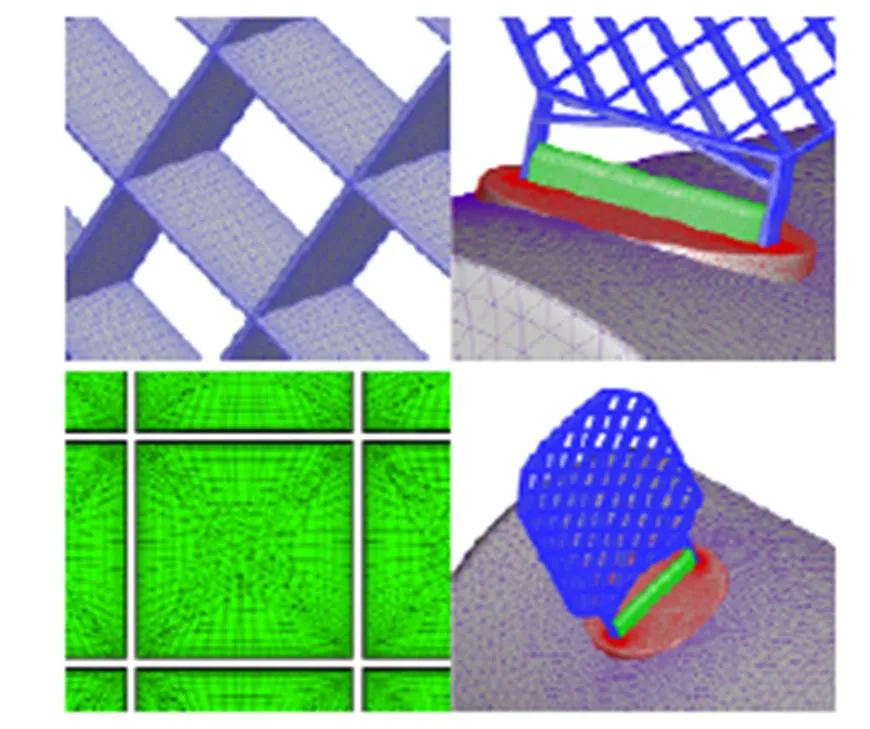
圖6 網格分布

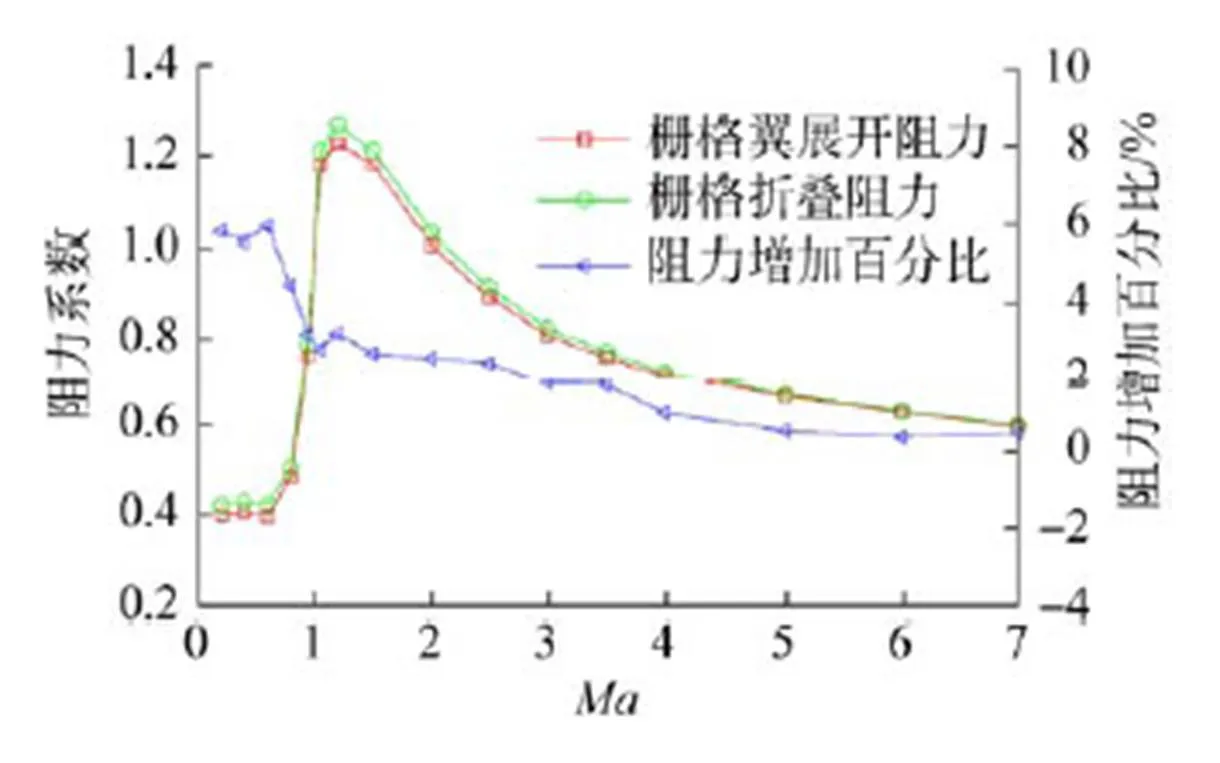
圖7 上升段阻力特性對比

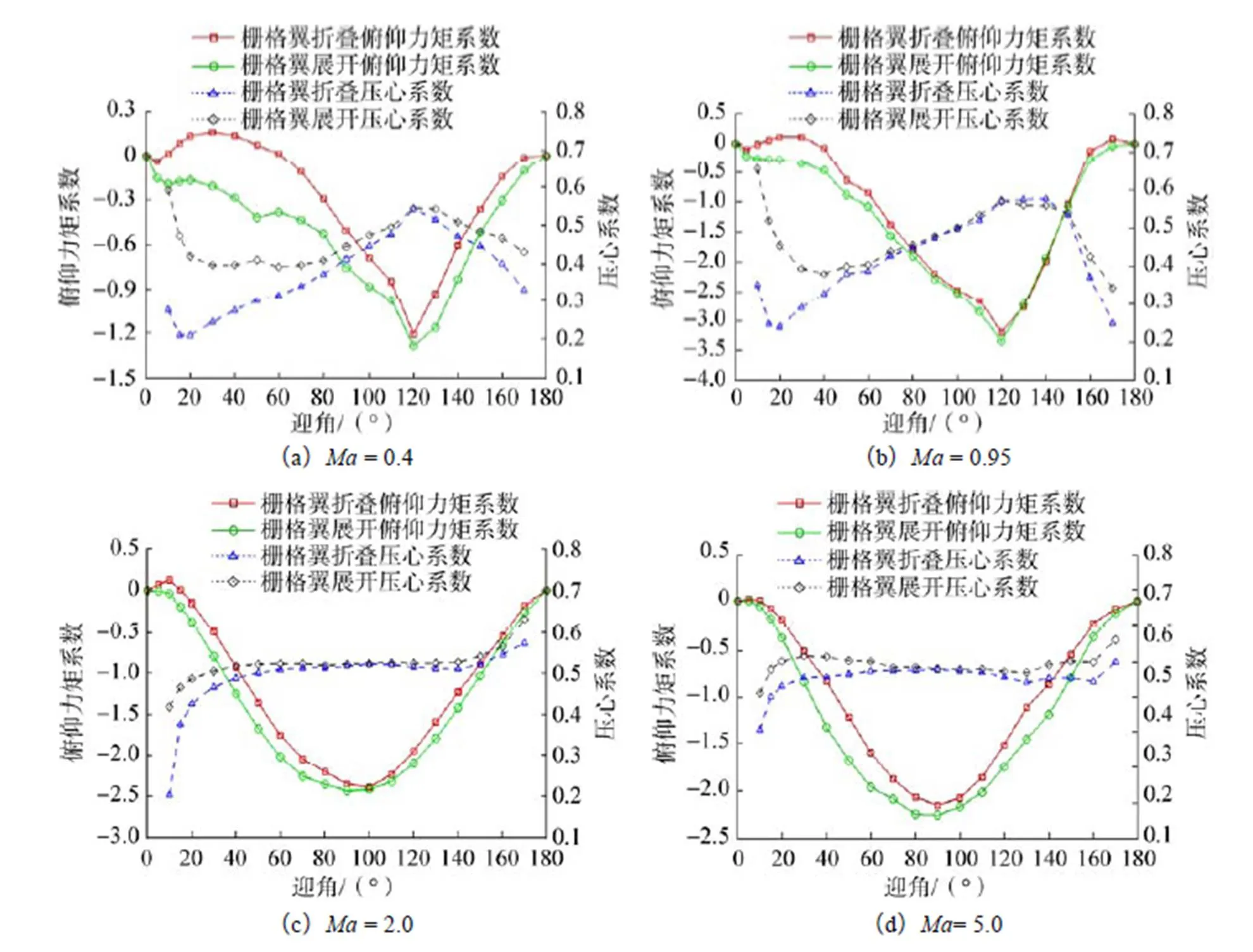
圖8 再入段不同馬赫數下氣動特性對比

3 火箭芯一級殘骸落點散布初步仿真

3.1 基于蒙特卡羅的落點散布分析方法

火箭芯一級殘骸再入返回過程中，干擾因素較多，為綜合分析相關因素的影響，采用經典的統計學試驗方法—蒙特卡羅方法，分析預測落點散布范圍。

基于蒙特卡羅的彈道仿真分析方法，其主要步驟為：

1）對影響火箭芯一級落點散布的影響因素進行分析，確定其概率分布，建立干擾因素偏差概率模型；

2）根據各個干擾因素偏差出現的概率進行隨機抽樣，產生符合干擾變量概率分布規律的抽樣值；

3）將干擾因素抽樣值代入彈道數學模型進行仿真分析；

4）重復2、3步，建立大量落點散布樣本，利用數理統計理論進行統計分析。

概率模型的可靠程度直接影響仿真分析結果，要求所建立的概率模型，能夠正確反映各干擾因素的實際情況和概率分布。在本文的火箭芯一級落點散布分析中，考慮了氣動力偏差、火箭芯一級質量慣量特性偏差、火箭一二級分離點參數偏差和大氣環境偏差影響。

3.2 落點散布仿真結果分析

針對火箭芯一級加裝柵格翼后的氣動布局方案，開展了殘骸落點散布的仿真分析，分析了無控柵格翼對火箭芯一級殘骸再入姿態和落點散布范圍的影響，每種方案進行了10 000條彈道的蒙特卡羅拉偏仿真。

圖9給出了火箭芯一級殘骸加裝柵格翼進入大氣層后基準彈道仿真曲線。可以看出，火箭上升段一二級分離后，芯一級殘骸由于慣性會繼續向前飛行，到達一定高度后，由于地球引力作用，開始向大氣層再入。火箭芯一級殘骸進入大氣層后，飛行姿態振蕩收斂，最終落地迎角在0°附近，與之前氣動性能分析結果相一致。在大氣層內，火箭芯一級殘骸由于氣動阻力作用，馬赫數逐漸降低，落地時馬赫數約為0.4。

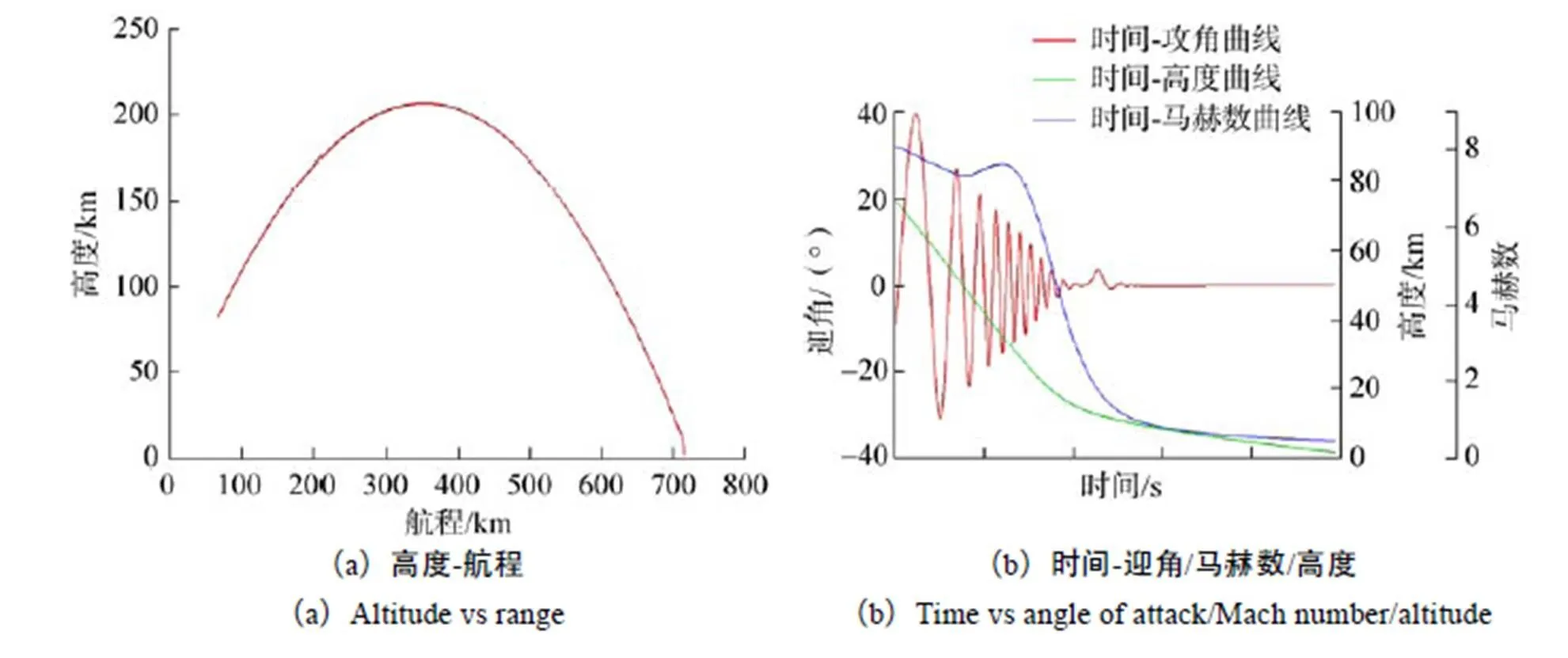
圖9 有柵格翼火箭芯一級殘骸基準彈道曲線

表1給出了火箭芯一級殘骸有無柵格翼6自由度蒙特卡羅拉偏仿真結果的落點參數對比，可以看出，有柵格翼外形的所有落點參數散布范圍都要小于無柵格翼外形，落點縱向和側向航程的均方差約為無柵格翼外形的1/2.5，落地時刻的均方差約為無柵格翼外形的1/2，有柵格翼外形由于進入大氣層后飛行迎角振蕩收斂，導致了氣動阻力比無柵格翼外形明顯減小，從而飛行時間減小，有柵格翼外形落地總迎角在0°附近。

表1 拉偏仿真落點參數統計結果對比

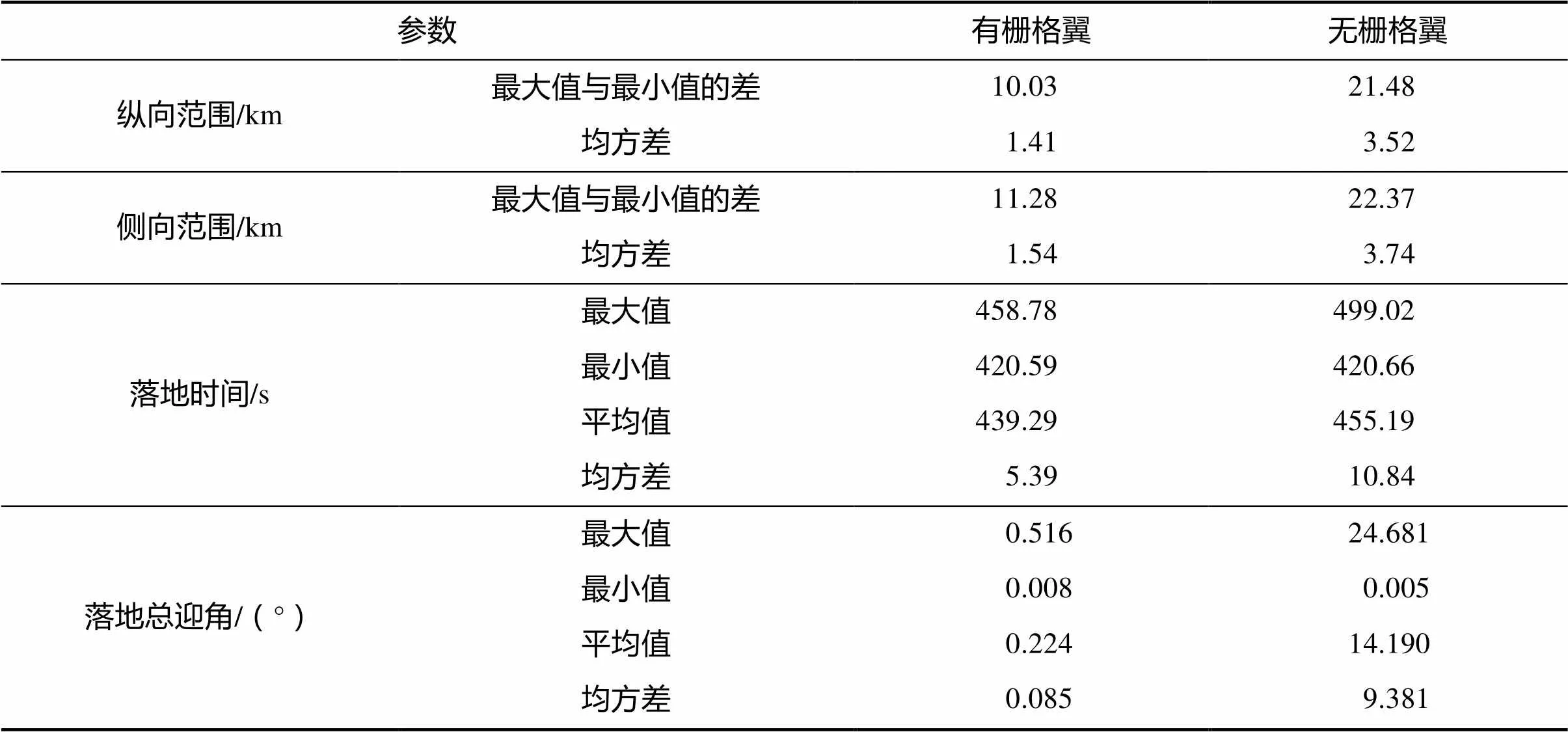
Tab.1 Comparison of statistical results of different simulation parameters

圖10給出了有無柵格翼外形火箭芯一級殘骸落點散布拉偏仿真結果，可以看出，增加柵格翼后，由于火箭芯一級殘骸自身具有氣動穩定性，火箭芯一級殘骸落點的散布范圍明顯縮小，對于無柵格翼外形，仿真得到的落點散布范圍約為21.48km × 22.37km，該數值與文獻[2]給出的40km × 30km落區范圍上存在一定差異，主要原因是本文考慮的拉偏量與實際火箭拉偏量存在一定差異造成的。但總體來說，殘骸落點分布的整體趨勢與文獻相一致。在有無柵格翼落點散布范圍對比分析中，采用相同的拉偏方式，仿真獲得了加裝柵格翼后火箭芯一級殘骸落點散布范圍，約為10.03km × 11.28km，與無柵格翼外形相比，落點散布面積減小了約76%。

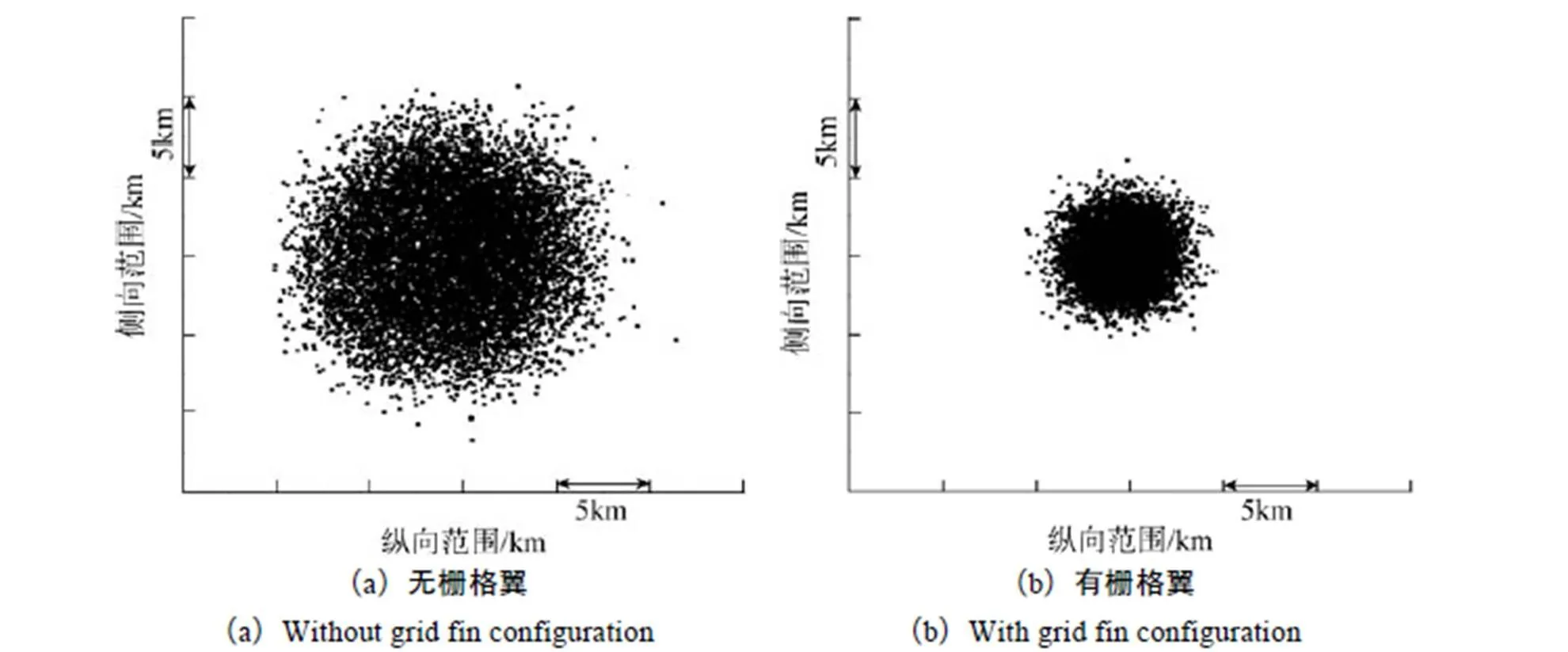
圖10 火箭芯一級殘骸有無柵格翼落點散布范圍對比

圖11給出了彈道拉偏仿真得到的火箭芯一級殘骸有無柵格翼外形迎角—時間歷程散布曲線，可以看出，對于無柵格翼火箭芯一級殘骸，在中等迎角范圍內俯仰靜穩定，在小迎角范圍內存在多個靜穩定配平點，分別的±20°和0°附近；而火箭芯一級殘骸加裝柵格翼后，俯仰方向具有氣動穩定性，再入過程中配平迎角在0°附近，進入大氣層后飛行迎角振蕩收斂，從而使得帶柵格翼火箭芯一級殘骸落點散布的范圍明顯減小。

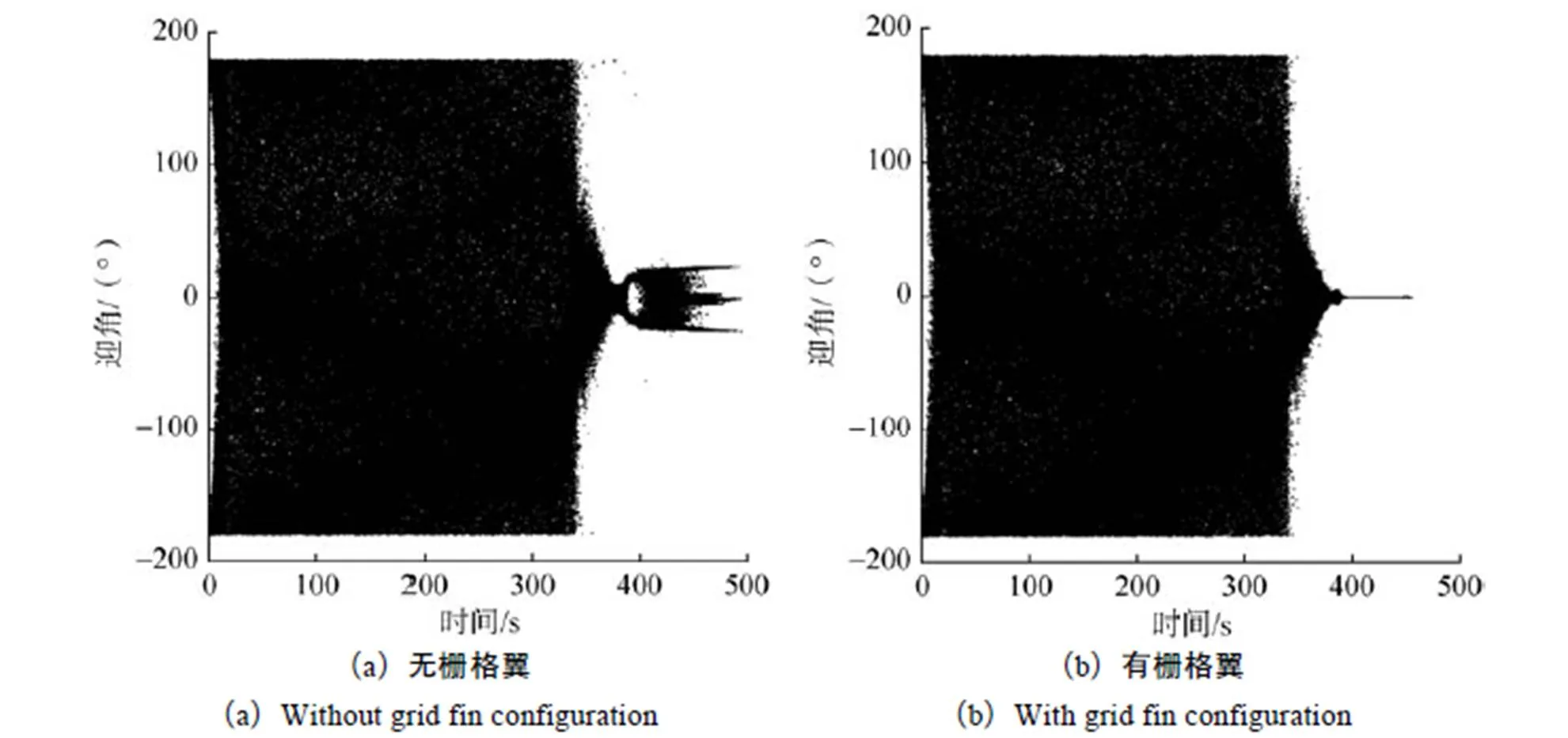
圖11 火箭芯一級殘骸有無柵格翼迎角—時間歷程散布對比

4 結束語

利用柵格翼氣動效率高、能夠改變靜穩定性的特點，本文探索了其在減小火箭芯一級殘骸落點散布范圍上的應用。本文設計的柵格翼單片質量約為150kg，上升段折疊安裝，阻力增量較小；再入段柵格翼展開后，小迎角范圍內火箭芯一級殘骸壓心后移明顯，氣動穩定性明顯增強，配平迎角在0°附近，使得飛行迎角在進入大氣層后迅速振蕩收斂；蒙特卡羅彈道仿真結果顯示，殘骸落點散布面積減小約76%。本文研究的火箭芯一級加裝柵格翼方案，可以大幅減小殘骸落點散布范圍，不需要增加額外復雜的控制機構，具有廣闊的應用前景。

目前本文研究的火箭芯一級加裝柵格翼方案仍屬于無控飛行，下一步將設計柵格舵構型，降低上升段附加質量，開展柵格舵控制效率分析，規劃火箭芯一級助推器下落彈道，設計制導率，結合姿控發動機復合控制技術，實現火箭芯一級的落點精確控制與回收。

[1] 楊勇, 王小軍, 唐一華. 重復使用運載器發展趨勢及特點[J]. 導彈與航天運載技術, 2002(5): 15-19. YANG Yong, WANG Xiaojun, TANG Yihua. Development Trends and Characteristics of Reusable Launch Vehicles[J]. Missiles and Space Vehicles, 2002(5): 15-19. (in Chinese)

[2] 肖松春, 宋建英, 安學剛. 基于蒙特卡洛方法的運載火箭殘骸落區劃定[J]. 裝備指揮技術學院學報, 2010, 21(4): 66-70. XIAO Songchun, SONG Jianying, AN Xuegang. Describing Area of Level Point of Rocket′s Debris Based on Monte-carlo Method[J]. Journal of the Academy of Equipment Command & Technology, 2010, 21(4): 66-70. (in Chinese)

[3] 汪小衛, 張普卓, 吳勝寶, 等. 運載火箭子級回收技術研究[J]. 航天返回與遙感, 2016, 37(3): 19-28. WANG Xiaowei, ZHANG Puzhuo, WU Shengbao, et al. Recovery Technology of Launch Vehicle Stage[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(3): 19-28. (in Chinese)

[4] 黃偉. 運載火箭傘降回收著陸技術概述[J]. 航天返回與遙感, 2017, 38(3): 1-12. HUANG Wei. The Summary of Launch Vehicle Parachute Recovery and Landing Technologies[J]. Spacecraft Recovery & Remote Sensing, 2017, 38(3): 1-12. (in Chinese)

[5] 趙祖虎. 航天飛機助推器輕型回收系統[J]. 航天返回與遙感, 1997, 18(4): 3-8. ZHAO Zuhu. Space Shuttle Solid Booster Lightweight Recovery System[J]. Spacecraft Recovery & Remote Sensing, 1997, 18(4): 3-8. (in Chinese)

[6] CARL M, ASHLEY T, JAMES B, et al. Ares I-x Separation and Reentry Trajectory Analyses[C]//AIAA Atmospheric Flight Mechanics Conference. AIAA 2011-6462. Portland, Oregon, 2011.

[7] ANTHONY T, PHILLIP D, ANTHONY T, et al. An Overview of the Landing System for the K-1 Launch Vehicle, Parachutes and Airbags[C]//AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. AIAA 1997-1515. SanFrancisco, CA, 1997.

[8] BARRY H, DANIEL T. Final Approach and Landing for a Winged Reusable Booster[C]//15th AIAA International Space Planes and Hypersonic System and Technologies Conference, AIAA 2008-2566, Dayton, Ohio, 2008.

[9] 鄭雄, 楊勇, 姚世東, 等. 法爾肯9可重復使用火箭發展綜述[J]. 導彈與航天運載技術, 2016(2): 39-46. ZHENG Xiong, YANG Yong, YAO Shidong, et al. Survey and Review on Development of Falcon 9 Reusable Rocket[J]. Missiles and Space Vehicles, 2016(2): 39-46. (in Chinese)

[10] 馮韶偉, 馬忠輝, 吳義田, 等. 國外運載火箭可重復使用關鍵技術綜述[J]. 導彈與航天運載技術, 2014(5): 82-86. FENG Shaowei, MA Zhonghui, WU Yitian, et al. Survey and Review on Key Technologies of Reusable Launch Vehicle Abroad[J]. Missiles and Space Vehicles, 2014(5): 82-86. (in Chinese)

[11] RAVINDRA K, NIKHIL V S, BALAKRISHNAN N. CFD Simulation of the Grid Fin Flows[C]//The 31stAIAA Applied Aerodynamics Conference. San Diego, CA, June 24-27, 2013.

[12] THEERTHAMALAI P. Effect of Geometric Parameters on the Aerodynamic Characteristics of Grid-fin Cells at Supersonic Speeds[R]. AIAA 2007-690.

[13] LIN H, HUANG J C, CHENG C. Navier-stokes Computations for Body/Cruciform Grid Fin Configuration[J]. Journal of Spacecraft and Rockest, 2003, 40(1): 30-38.

[14] 任懷宇, 蔡昱, 孫洪森. 高超聲速柵格翼氣動特性研究[J]. 宇航學報, 2010, 31(1): 44-49. REN Huaiyu, CAI Yu, SUN Hongsen. Study on Aerothermodynamics of Hypersonic Grid Fin[J]. Journal of Astronautics, 2010, 31(1): 44-49. (in Chinese)

[15] 吳曉軍, 陳紅全, 鄧有奇, 等. 柵格翼繞流數值模擬研究[J]. 空氣動力學報, 2009, 27(1): 78-82. WU Xiaojun, CHEN Hongquan, DENG Youqi, et al. CFD Analysis of Grid Fins[J]. Acta Aerodynamica Sinica, 2009, 27(1): 78-82. (in Chinese)

[16] 張耀冰, 鄧有奇, 吳曉軍, 等. DLR-F6翼身組合體數值計算[J]. 空氣動力學報, 2011, 29(2): 163-169. ZHANG Yaobing, DENG Youqi, WU Xiaojun, et al. Drag Prediction of DLR-F6 using MFlow Unstructured Mesh Solver[J]. Acta Aerodynamica Sinica, 2011, 29(2): 163-169. (in Chinese)

[17] CHEN J T, ZHANG Y B, ZHOU N C, et al. Numerical Investigations of the High-lift Configuration with MFlow Solver[J]. Journal of Aircraft, 2015, 52(4): 1051-1062.

[18] MA M S, DENG Y Q, ZHENG M, et al. Navier-stokes Computations for a Grid Fin Missile[C]//The 23rdAIAA Applied Aerodynamics Conference. Toronto,Canada, 2005.

[19] MONTGOMERY C, HUGHSON, ERIC L B. Transonic Aerodynamic Analysis of Lattice Grid Tail Fin Missiles[C]//The 24thApplied Aerodynamics Conferernce. San Francisco, California, 2006.

[20] ABATE G, WINCHENBACH G, HATHAWAY W. Transonic Aerodynamic and Scaling Issues for Lattice Fin Projectiles Tested in a Ballistic Range[C]//Proceedings of the 19thInternational Symposium of Ballistic. Interlaken, Switzerland, 2001.

[21] ZENG Y, CAI J S, DEBIASI M, et al. Numerical Study on Drag Reduction for Grid Fin Configurations[R]. AIAA 2009-1105.

Application Research of Grid Fin on Reducing the Falling Point Distribution for the Debris of Rocket

JIA Hongyin XU Mingxing ZHANG Peihong WU Xiaojun HE Zhengchun

（China Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang, 621000, China）

The characteristics of grid fin with high efficiency and high aerodynamic drag are applied to reduce the falling point distribution for the first stage debris of rocket. First of all, the numerical methods for the aerodynamic characteristics of gird fin are introduced. The reliability of the numerical method is verified by comparison of the results with the experimental data. And then the research on the design of the gird fin for the rocket booster is carried out. The aerodynamic performance of the first stage debris of rocket with grid fin at subsonic and supersonic is analyzed. The falling point distribution range of the first stage debris before and after installing grid fin are compared by six degrees of freedom Monte Carlo trajectory simulation. The results indicate that the drag increment is very small when the rocket with folded grid fin rises up. The drag increases less than 2% at supersonic condition. When making a reentry with the grid fin unfolded, the first stage debris has aerodynamic stability and trim angle of attack near 0 degree. The attitude of the debris convergence rapidly during reentry. After installation of the grid fin, the range of falling point distribution of the first stage debris is reduced by 76%. The grid fin has wide application prospects in reducing the falling point distribution for the first stage debris of rocket.

grid fin; aerodynamic stability; falling point distribution; trajectory simulation; rocket; aerospace recovery

V525

A

1009-8518(2018)06-0021-09

10.3969/j.issn.1009-8518.2018.06.003

2018-05-05

國家重點研發計劃戰略高技術重點專項（17H86303ZT001018）

賈洪印，男，1985年生，2011年獲中國空氣動力研究與發展中心碩士學位，助理研究員。主要研究方向為計算空氣動力學。E-mail：hongyinjia@foxmail.com。

（編輯：龐冰）