亞音速壁板弱非線性動力學模型響應預測

黎昭文， 李 鵬， 楊翊仁

(西南交通大學 力學與工程學院， 四川 成都 610031)

0 引 言

研究表明，高速列車在運行時， 其車身蒙皮等壁板結構與流體之間存在強耦合作用會出現嚴重的氣動彈性問題[1].事實上， 氣動彈性力學系統的研究需要同時關注結構與氣動力兩者之間的耦合作用.針對該問題， 科研人員做了大量研究[2-8].研究表明，對高速列車運行這類低馬赫數流動問題， 其車身壁板上的氣動力可用線性模型表征，在考慮壁板結構非線性環節后的氣動彈性動力學模型可用一類典型的非線性VanderPol-Duffing方程來表征.故， 本研究擬基于Volterra級數采用脈沖響應法對模型系統進行辨識， 并對該模型系統的動力學響應進行預測， 從而建立該類氣動彈性問題的響應分析方法.

1 Volterra級數理論

研究發現，Volterra級數適用于時不變弱非線性系統的建模，其可在任意精度上逼進集上的連續函數[9].任意時不變的離散系統對任意輸入u[n]的響應y[n]可用無限項的多維卷積分描述，

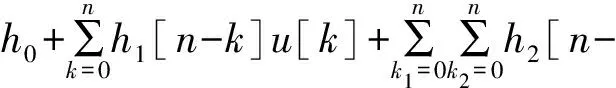
k1,n-k2]u[k1]u[k2]+…+

n-km]u[k1]u[k2]…u[km]+…

(1)

式中，n=0,1,2,…，是離散時間變量，h0是定常狀態響應，hm[n-k1,n-k2，…，n-km]是系統的m階核.若能識別出系統的各階核，則系統對于任意輸入的響應都可以通過上述卷積求得.

各階核的識別過程是Volterra級數模型建立的關鍵步驟.研究顯示，核識別的方法包括脈沖響應法、階躍響應法和準階躍響應法等[10].本研究擬采用脈沖響應法識別模型系統的各階核.

設該模型系統的定常狀態h0=0，則式(1)可寫為如下的二階截斷形式，

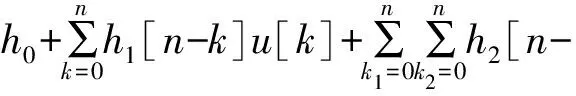
k1,n-k2]u[k1]u[k2]

(2)

定義離散時間域內一維單位脈沖、二維單位脈沖為，

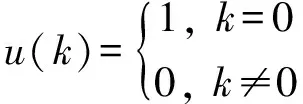
(3)

u(τ1)=u(τ1-k1)+u(τ1-k2)， 0≤k1≤k2

(4)

按識別要求分別施加脈沖信號于式(2)，可得其一階核的表達式為，

(5)

式中，當y0[n]為零時施加信號(1)的響應，y2[n]為零時施加雙倍幅值信號(1)的響應.

模型系統的二階核的表達式為，

h2[n-k1,n-k2]

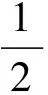
(6)

式中，y1[n-k1,n-k2]為施加信號(4)的響應，y0[n-k1]和y1[n-k2]分別為在k1和k2時刻施加信號(3)的響應.

一階核h1[n]為時間n的一維函數，表示非線性系統的線性子系統特性，也可表征一定的非線性特性，且比非線性系統純線化后的線性核更加合理.二階核是關于時間n和時移k1-k2的二維函數序列.

2 壁板模型的動力學系統與響應預測

2.1 壁板模型的動力學系統與方程

兩端簡支的黏彈性二維壁板模型如圖1所示.壁板上表面有沿軸向的不可壓縮亞音速氣流，氣流密度及速度分別為ρ∞與U∞，壁板上表面作用有擾動氣流及基座擾動所致簡諧激勵力.

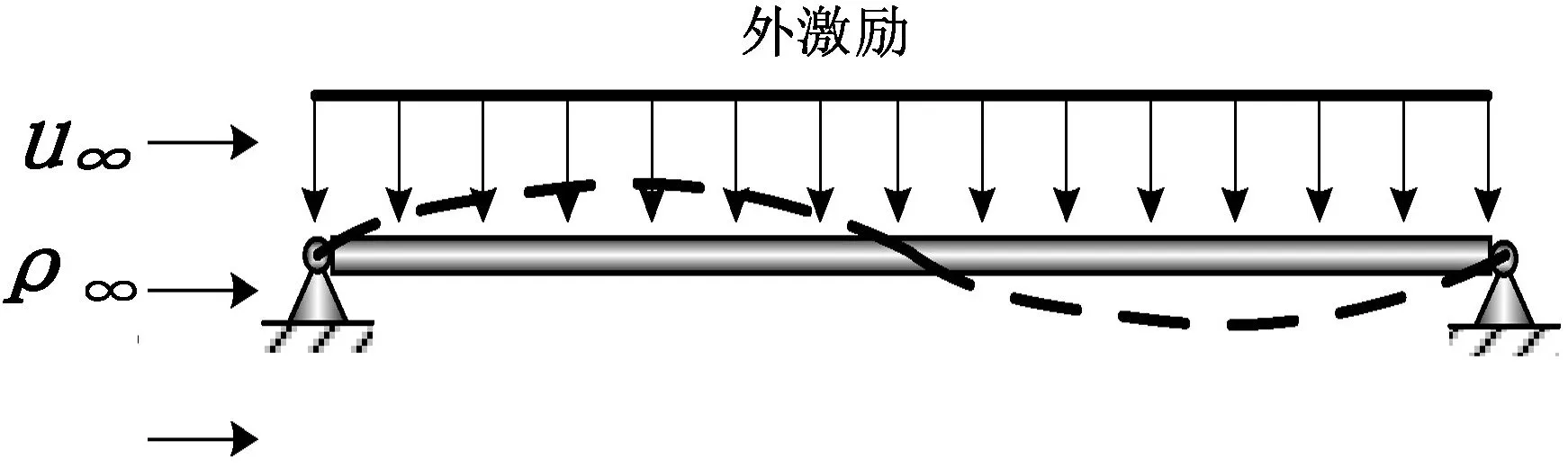
圖1二維壁板模型

描述該模型的氣動彈性系統的無量綱動力學方程[1]為，

(7)

式中，質量m=ms+mf、剛度系數k=ks+kf，其中下標s表示結構相關項，f表示與流體相關的附加項，其隨流體的密度與速度的改變而變化；阻尼系數μ和非線性項系數k3只與結構參數相關；外激勵幅值F0和外激勵頻率ω均與擾動氣動力和基座激擾有關[11].

式(7)所表征的方程可視為弱非線性系統，可用其對模型的動力學系統響應進行預測.

2.2 非線性響應預測

首先，將式(7)右端項替換為脈沖激勵P，并將式(7)降階為一階微分方程組，

(8)

表1 計算參數

基于表1的參數，圖2(a)給出模型系統起步階段的響應的數值計算及理論預測解，圖2(b)～(d)給出了模型系統穩態階段的數值計算及預測解.

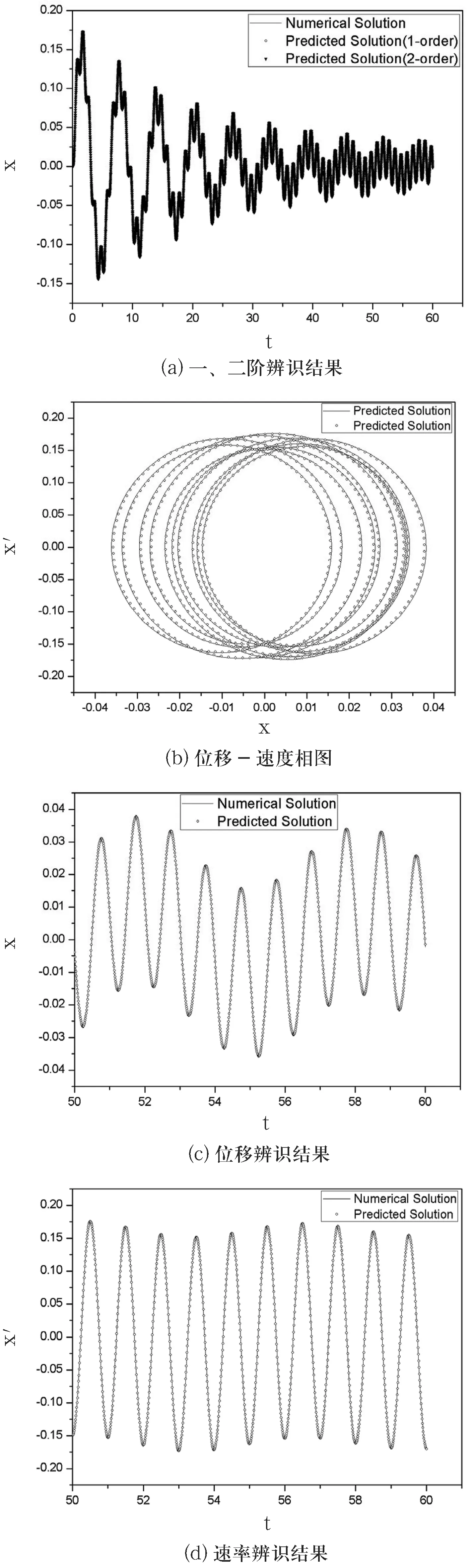
圖2 模型系統的動力學響應預測結果

由圖2(a)可知，采用一階核可較好地預測該模型的響應，且對其起步階段及穩定階段的響應均有很好的預測.因二階核對一階核的修正效果有限，故本分析中僅使用一階核進行系統的響應預測.

為研究模型系統的參數對響應預測的影響，需要對方程(7)中的可變參數進行分析以確定其合理的變化范圍，從而保證獲得較好的識別效果.

2.2.1 流場參數.

流場參數可由質量m和剛度系數k表征.計算發現，隨著m值的變大，其響應的預測效果將會逐漸變差，結果如圖3所示.從圖3可知，系統的響應預測值在峰值處已經出現了明顯的差別.同時，由計算可知，當k相對較大時，系統響應識別效果較好，結果如圖4所示.從圖4可知，當k逐漸變小并趨于零時，系統的響應預測效果會顯著變差.這主要是由于系統處于零剛度的失穩臨界狀態.故，相對較小的m和相對較大的k能夠保證模型系統有較好的預測效果.

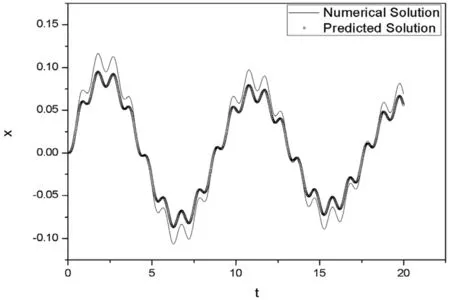
圖3m=2時位移預測結果

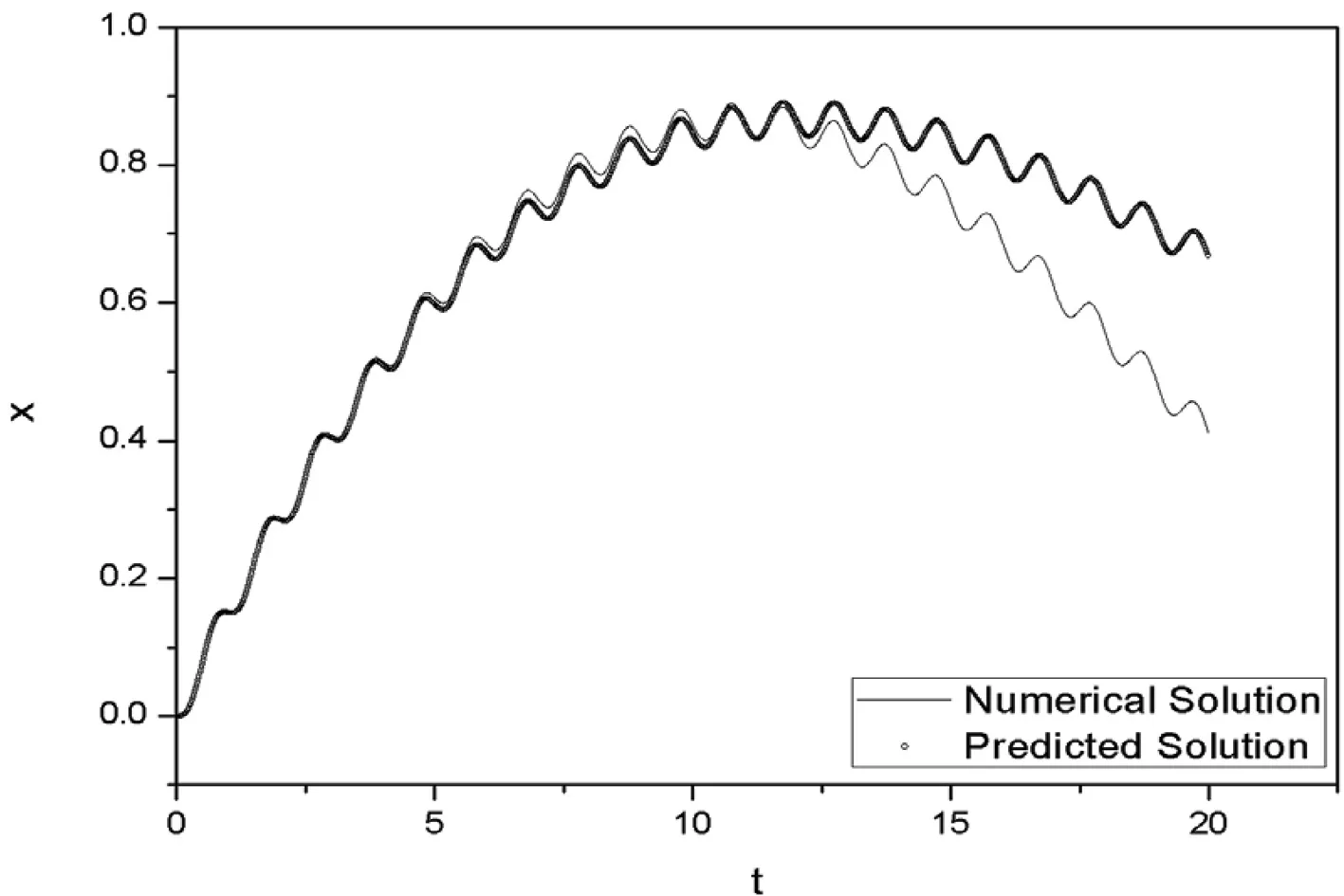
圖4k=0.01時位移預測結果

2.2.2 結構參數.

結構參數主要由阻尼系數μ和非線性項系數k3表征.計算發現，預測效果對μ值變化并不敏感，但會影響系統趨于穩態的時間，即μ越大其進入穩態的時間就越快，圖5給出了μ=1時的系統響應預測結果，進入穩態時間與μ=0.1相比明顯變短.同時，由計算可知，隨著k3的增大預測效果會變差，圖6給出了k3=10時系統起始段預測結果.由圖6可知，為保證模型系統有較好的預測效果，應使k3相對較小.

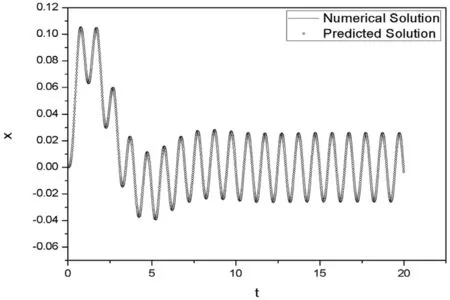
圖5μ=1時位移預測結果

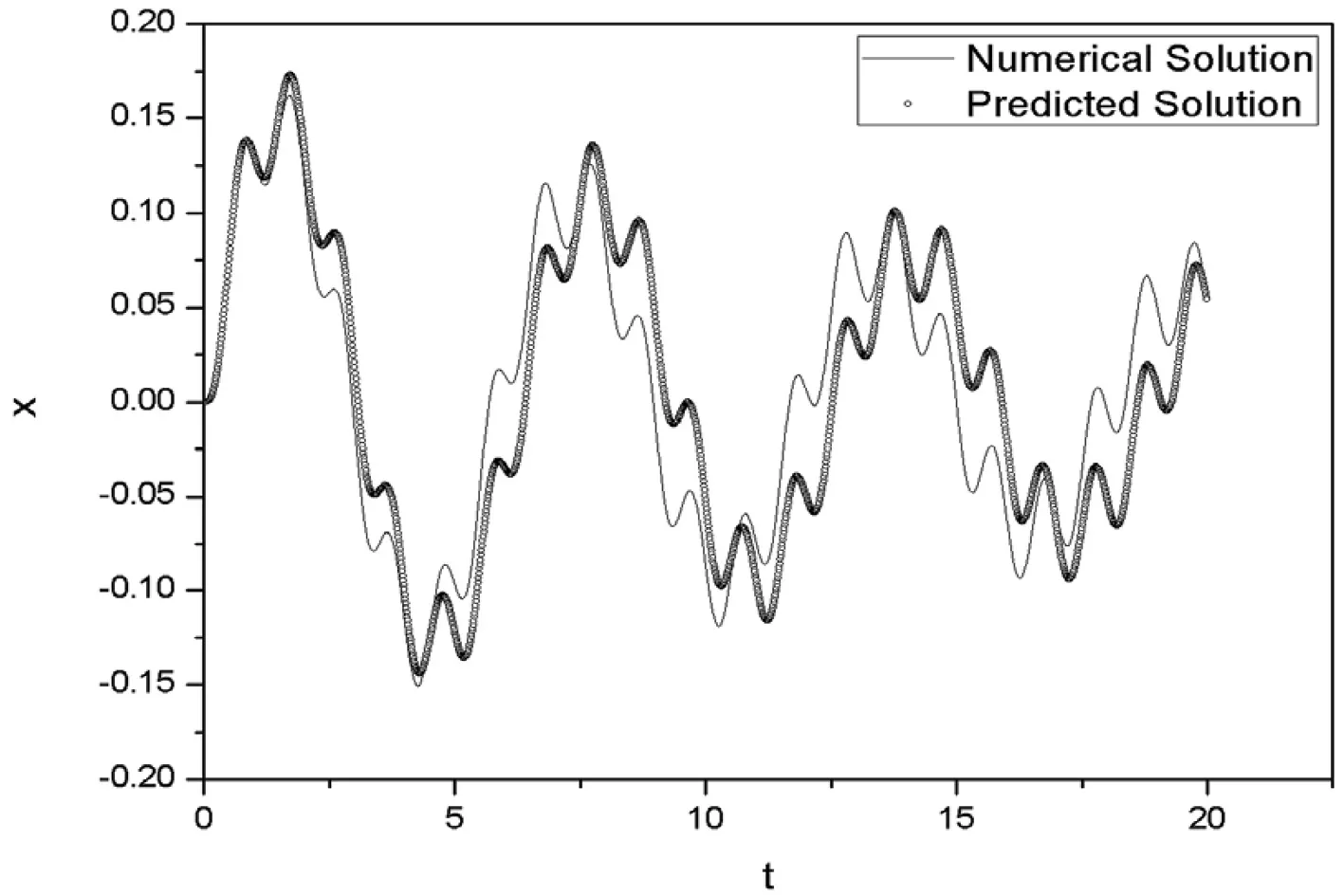
圖6k3=10時位移預測結果

2.2.3 激勵參數.

激勵參數主要由外激勵幅值F0和外激勵頻率ω表征.計算發現，F0的大小對模型預測結果的影響不明顯，但對系統的位移幅值的影響較大，結果如圖7所示.同時，由計算可知，ω值越小，預測效果越差，結果如圖8所示.據此可知，相對較大ω值可保證模型系統有較好的預測效果.

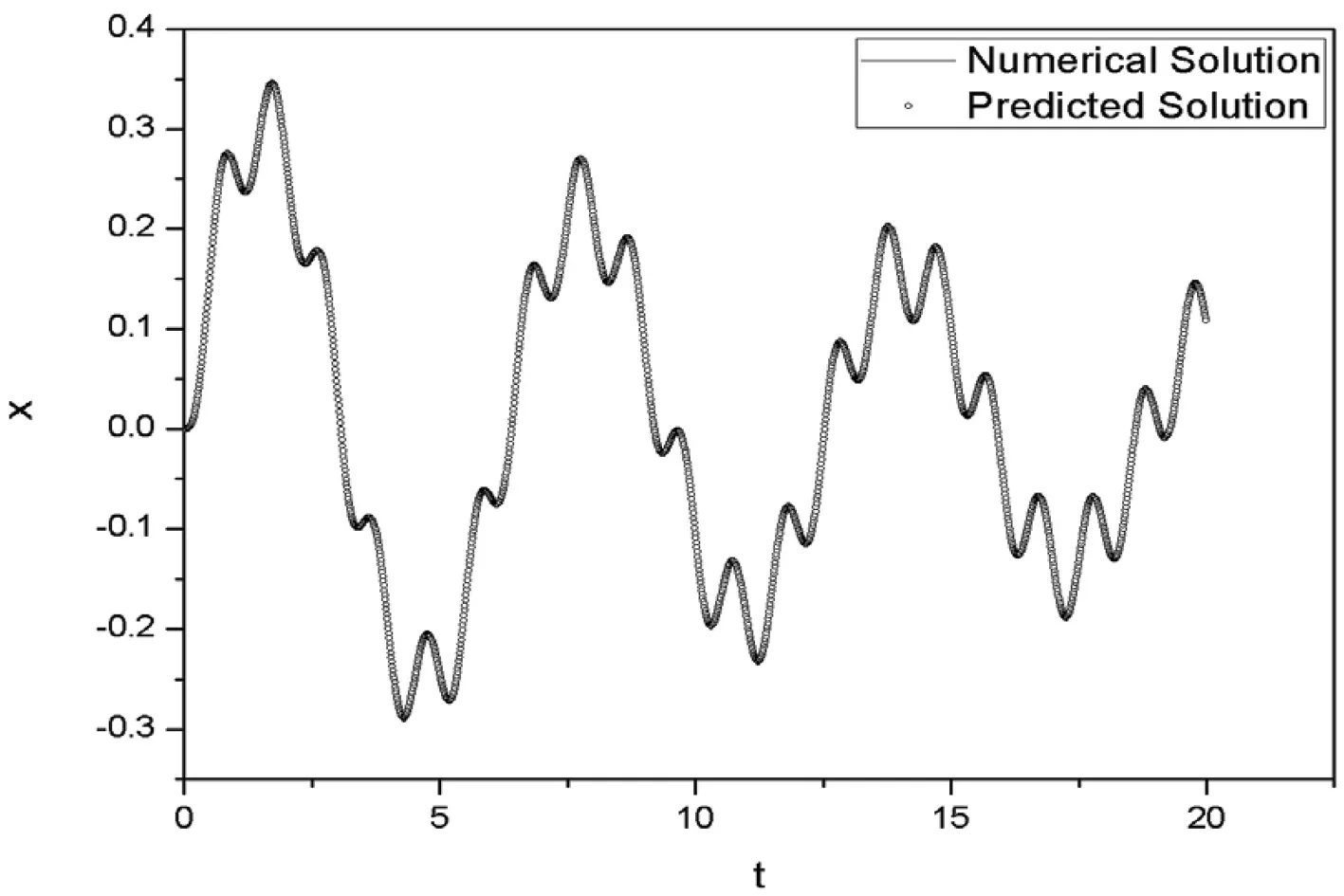
圖7F0=2時位移預測結果

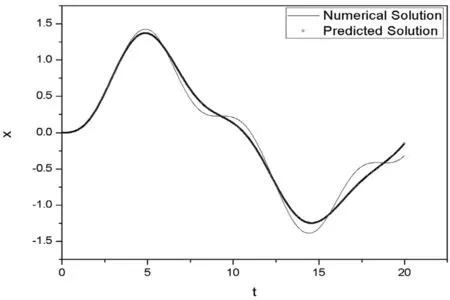
圖8 ω=0.1 π位移預測結果

3 結 論

本研究選取表征亞音速壁板非線性動力學模型系統的VanDerPol-Duffing方程，并對其進行了研究，基于Volterra級數對模型進行核識別并建立相應的系統以進行動力學響應預測.研究表明：對該類弱非線性問題，基于一階核所構建的Volterra模型對系統的響應有較好的預測效果；系統的阻尼系數μ和外激勵幅值F0對預測精度無明顯影響，系統的質量m和非線性項系數k3的值相對越大，則預測精度越差，剛度系數k和外激勵頻率ω的值相對越小，其預測精度越差.