基于WSN的全同態數據加密聚合方案
王彩芬,成玉丹,劉 超
(西北師范大學 計算機科學與工程學院,蘭州 730070)
0 概述
無線傳感器網絡(Wireless Sensor Network,WSN)的基本結構有樹形和簇形,均由若干個傳感器節點和一個基站(Base Station,BS)組成,通信方式是無線鏈路通信,并且能夠實時監測、感知和收集網絡覆蓋范圍內的各種環境信息[1]。傳感器能量受限,存儲和計算能力較小,但基站有固定的能量來源,是整個網絡的核心,存儲空間大,計算能力強。
目前,國內外學者針對WSN中數據的安全傳輸問題進行了一定研究。早期采用基于對稱加密機制的點到點數據聚合算法[2],該算法的優點是容易實現且方便快捷,但其會造成密鑰和明文的泄露。為得到較好的安全性能,文獻[3]提出2-DNF非對稱密碼系統,通過同態的加乘運算實現數據的聚合,但其在數據驗證和防止抵賴等方面仍存在局限性。此后,又出現了多個針對該方案的改進方法。文獻[4]提出能夠抵御內部攻擊的數據聚合方案。文獻[5]提出在WSN中基于同態原語的數據聚合方案。文獻[6]在數據的機密性和完整性上進行改進,提出基于同態加密的WSN數據融合的機密性和完整性方案。文獻[7]提出基于同態加密的可驗證隱私數據聚合方案。文獻[5-7]對2-DNF非對稱密碼系統的計算效率和安全性能均做了改進,但仍有不足之處:文獻[5]需要一個額外的可信第三方來分發保密干擾因子,而且方案的構造方式復雜;文獻[6]在抵御內部攻擊上存在局限性;文獻[7]通過聚合器本身對每一個傳感器節點分配干擾因子,計算復雜度高,并且其采用ElGamal方案加密隱私數據,僅滿足了乘法同態性,并不滿足全同態性。
針對上述方法的不足,本文在文獻[7]的基礎上,基于簇的網絡結構提出WSN中全同態的數據加密聚合方案。采用具有全同態性的DGHV[8]方案加密隱私數據,同時將包含節點身份信息的簽名嵌入到密文中,通過簽名驗證其正確性,使方案具有抵抗數據被篡改、追查并糾正錯誤數據的能力。本文方案以簇為單位,通過聚合器為簇內的傳感器節點分發保密干擾因子,以避免由第三方帶來的安全問題。
1 預備知識
1.1 符號和參數定義
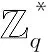
給定安全參數λ,參數的設置為:ρ表示噪音長度,η表示私鑰長度,γ表示公鑰長度,τ表示公鑰中整數的個數。為滿足該方案的安全性,上述參數需滿足如下條件:
1)ρ=ω(lbλ),使方案能夠抵抗噪音的蠻力攻擊。
2)η≥ρΘ(λlb2λ),使方案能夠支持足夠深的電路同態評估。
3)γ=ω(η2lbλ),使方案能阻止各種基于格的攻擊,比如近似的最大公因子(Greatest Common Divisor,GCD)問題。
4)τ≥γ+(ωlbλ),使方案能夠在GCD中使用剩余的哈希引理。
1.2 雙線性映射
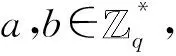
1)雙線性:對任意的u,v∈G1,滿足e(ua,vb)=e(u,v)ab。
2)非退化性:e(u,v)≠1G2,其中,1G2為G2中的單位元。
3)可計算性:對任意u,v∈G1,存在有效算法能夠計算e(u,v)。
1.3 困難問題假設
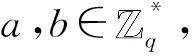
定義3(GCD問題)[8]參數為ρ、η、γ,p為一個隨機的ηbit的素數,x0=pq0,q0∈Z∩[0,2γ/p)。
求p的過程就是GCD問題。
1.4 全同態加密
定義4(全同態加密)[10]同態加密指在不解密密文的情況下,通過對密文執行操作來實現對明文的加密,且其結果一致,這里的全同態是指同時滿足加法同態和乘法同態。全同態加密方案中包含4個函數:KeyGen(λ),Encrypt(pk,m),Decrypt(sk,c)和Evaluate(pk,C,c)。其具體操作如下:
1)KeyGen(λ):根據安全參數λ產生公私鑰對(pk,sk)。
2)Encrypt(pk,m):在公鑰pk下把明文m加密成密文c。
3)Decrypt(sk,c):用私鑰sk解密密文c,得到明文m。
4)Evaluate(pk,C,c):輸入一個公鑰pk、電路C和一個密文元組c=〈c1,c2,…,ct〉,輸出另一個密文元組c。
1.5 DGHV方案
文獻[8]在Gentry方案的基礎上提出基于整數的全同態加密方案DGHV。其中各函數具體操作如下:
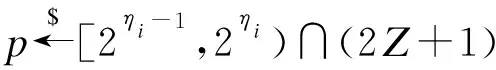
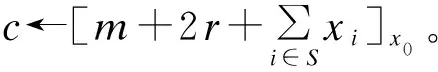
3)Decrypt(sk,c):輸出明文m←[[c]p]2。在解密過程中,首先通過密文模私鑰p,再模2即可得到1 bit的明文。
4)Evaluate(pk,C,c1,c2,…,ct):輸入公鑰pk、電路C和t個密文c1,c2,…,ct,其中,ci=Encrypt(pk,mi),i=1,2,…,t。輸出c*=Evaluate(pk,C,c1,c2,…,ct)且滿足Decrypt(sk,c*)=C(m1,m2,…,mt)。該算法集中體現了全同態加密的技術優勢,其通過門電路或者函數對密文進行任意操作后再解密,結果和操作明文的結果一致。
2 WSN中全同態數據加密方案
WSN的構建方式有多種,同時也產生了很多標準協議,如文獻[11]提出的標準聚合協議和文獻[12]中的網絡構建方式。假定本文方案中的聚合器擁有足夠的計算能力且是誠實但好奇的,即其可能會自主地做出一些錯誤的舉動,但不會與其他實體實施共謀攻擊[13]。同時,它能夠有效地完成方案中涉及的簽名驗證和解密操作。
目前提出的基于WSN的同態加密聚合方案僅僅實現了加法同態或乘法同態,文獻[7]以簇為單位分發干擾因子,但是每一個傳感器擁有獨立的干擾因子在很大程度上增加了方案的計算復雜度。由干擾因子的作用可知,它不涉及隱私信息,所以對它的改進主要是提高運算效率,降低計算復雜度。因此,本文在文獻[7]的基礎上,以簇為網絡結構,提出基于WSN的全同態數據加密聚合算法,實現隱私數據的加法和乘法同態。在干擾因子的分發過程中,每一個簇內的傳感器節點擁有相同的干擾因子,這樣既保證了方案能夠抵抗內部攻擊,又在很大程度上降低了計算復雜度。
2.1 網絡模型
本文采用的網絡模型是基于簇的網絡結構[14],如圖1所示。該結構的優點是將簇內節點的信息收集起來,統一向上一級節點傳送,能夠節省通信開銷,增強擴展性。網絡模型結構包含3類角色:基站BS,聚合器Agg和傳感器節點。整個網絡由多個非重疊的簇組成,每個簇中包含一個聚合器(簇頭)和n個傳感器節點。簇頭的功能是給簇內的每一個傳感器節點分發干擾因子π和身份標識ID,π只分發一次,即每一個傳感器節點具有相同的干擾因子,同時從傳感器節點接收加密的數據,將其聚合驗證后傳給BS;每一個傳感器節點將接收到的數據采用帶有干擾因子的DGHV方案加密,用自己的身份標識簽名,然后將密文發送給聚合器。
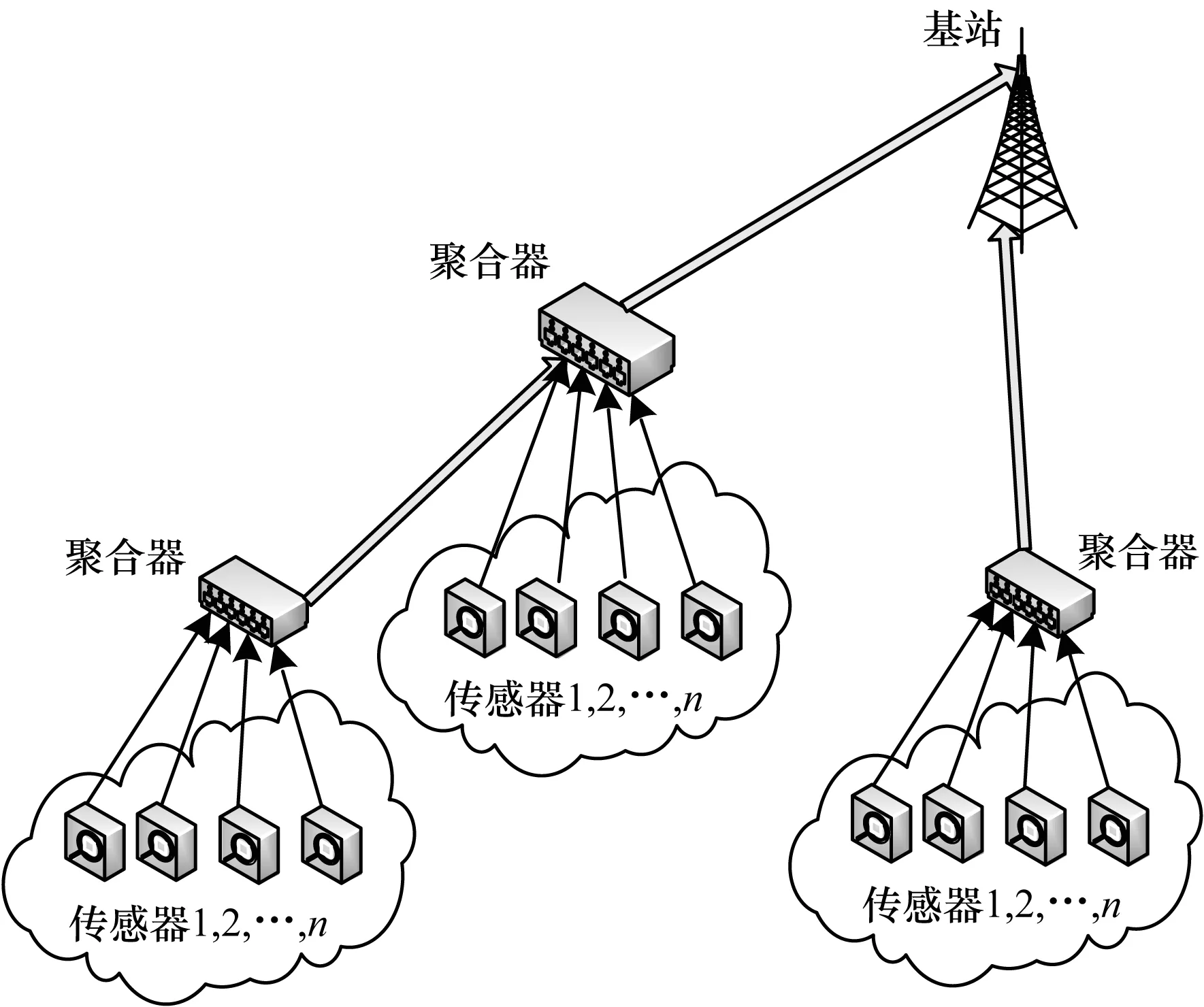
圖1 基于簇的網絡拓撲
2.2 方案設計
在基于簇的WSN構建完成后,加密聚合方案主要包括3個基本過程:系統建立階段,加密簽名階段和驗證聚合階段。在系統建立階段,聚合器作為整個簇的核心,為每一個傳感器節點分配身份標識ID、公私鑰和干擾因子π;在加密簽名階段,傳感器節點收集信息,利用公私鑰和π對消息加密,用ID對消息簽名;在驗證聚合階段,聚合器發出消息聚合的命令,每一個傳感器節點將加密的消息發送給聚合器,聚合器完成數據的聚合并進行驗證,若驗證成功,則進行相應操作得到消息,若驗證失敗,則檢測每一個節點的數據,并要求數據傳輸錯誤的節點重新傳輸數據。
2.2.1 系統建立階段
設在每一個簇內由一個聚合器控制著n個傳感器節點Ui(i=0,1,…,n-1)。聚合器作為密鑰生成中心,通過DGHV[8]方案和DF[15]方案為簇內的每一個節點分配公私鑰和干擾因子。該階段的2個基本操作如下:
1)密鑰生成階段:
(1)聚合器對控制的每一個傳感器節點分配身份標識IDi(i=0,1,…,n-1)。
(2)設置安全參數λ。
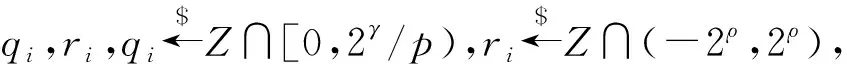
(4)生成N階乘法循環群G。
(5)在G中取生成元g。
(6)發布公鑰PK={pk,g},私鑰SK=p。
2)分配保密干擾因子πk(k=0,1,…,n-1,表示聚合器的個數)。
保密干擾因子的生成和分發過程是保密的,由于它不涉及核心消息mi,因此對它的保密要求比較低,而對其效率的要求較高。本文采用與DF[15]方案相同的分配方式,若聚合器為每一個傳感器都分配保密干擾因子,會增加計算復雜度。為降低計算復雜度,本文采用基于簇的傳感器網絡。假設以n個傳感器節點為一個簇,每一個簇分配一個保密干擾因子,即n個節點具有相同的干擾因子。聚合器(簇頭)的具體分配過程如下:


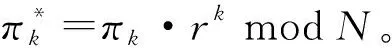
2.2.2 加密簽名階段
當傳感器節點Ui(i=0,1,…,n-1)收到聚合器發布的數據聚合的命令時,進行數據加密簽名的操作,在此過程中,傳感器節點可以對多次加密的數據實現全同態操作,再用身份標識IDi簽名,然后上傳給聚合器。具體過程如下:

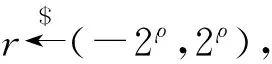
4)計算簽名σi=H(ci‖IDi)p及yi=gp。
5)將{ci,yi,σi}(i=0,1,…,n-1)發送至聚合器。
2.2.3 驗證聚合階段
在驗證聚合階段,聚合器首先對上傳的數據進行聚合,然后利用雙線性映射驗證其正確性,若驗證正確,則可以計算得到聚合的消息,具體操作如下:
1)聚合器接收所有傳感器節點Ui傳來的數據{ci,yi,σi}(i=0,1,…,n-1)。
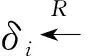
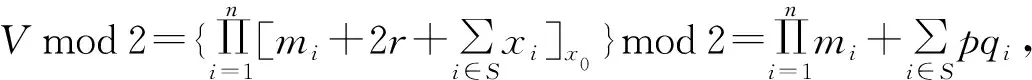
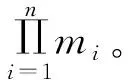
2.3 方案的正確性分析
本文方案的正確性分析具體如下:
1)簽名驗證的正確性:
2)聚合解密的正確性:
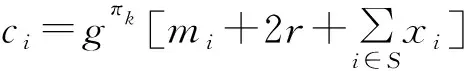
3 方案性能分析
3.1 全同態性分析
由于本文方案的加密算法運用了基于整數的全同態加密方案DGHV,因此其全同態性的詳細證明過程可參考文獻[8]。
3.2 保密干擾因子的安全性分析
在本文方案中,保密干擾因子πk(k=0,1,…,n-1表示聚合器的個數)是以簇為單位分配的,作用是在保證安全的基礎上提高方案的效率,其分配方式根據DF[15]方案構造,故本文方案中保密干擾因子安全性的詳細證明過程可參考文獻[15]。
3.3 基于AGCD問題的安全性證明
本文方案的安全性基于近似公因子(AGCD)難題和計算版本的Co-Diffie-Hellman問題。Co-Diffie-Hellman問題作為一些密碼系統困難問題的基礎,已經得到了證明和廣泛應用。本文對基于AGCD問題的安全性進行證明,主要證明思路是使用攻擊算法A來構造求解困難問題的算法B,該過程包括4個步驟:1)利用困難問題產生方案的公鑰;2)利用A構造求解p的商的最小比特位;3)執行Binary-GCD算法;4)恢復p。
定理1在第2.1節的方案中,固定參數(ρ,η,γ,τ)與安全系數λ。任意的攻擊者A以優勢ε攻擊加密方案,都可以轉化成求解器B以至少ε/2優勢求解參數為(ρ,η,γ)的近似AGCD問題。B的運行時間是tA、λ和1/ε的多項式,其中,tA是A的運行時間。
證明攻擊者A以ε的優勢攻擊本文方案,即A以ε的優勢輸入公鑰和密文(由本文方案的算法獲得公鑰和密文),正確輸出明文的概率至少是1/2+ε。
在參數為ρ、η、γ時,構造求解近似AGCD困難問題的求解器B,對于隨機選取的ηbit的奇整數p,求解器B需要從Dr,ρ(p)分布中獲得多個樣本來求解目標p。步驟如下:
步驟1創建公鑰。首先,求解器B為方案創建一個公鑰pk=〈x0,x1,…,xτ〉。
步驟2利用最低有效位(Least Significant Bit,LSB)子程序求解p的近似倍數的最小比特位。B調用以下子程序:
子程序Learn-LSB(z,pk)
輸入z∈[0,2γ),|rp(z)|<2ρ,公鑰pk=〈x0,x1,…,xτ〉
輸出qp(z)的最低有效位
1.For i=1 to poly(λ)/ε do://ε是A的整體優勢;
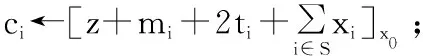
4.調用A訪問隨機預言機得到ai←A(pk,ci);
5.設置bi←ai⊕parity(z)⊕mi;
步驟3運用Binary-GCD算法[8]計算p。給定任意的2個整數z1=qp(z1)·p+rp(z1)和z2=qp(z2)·p+rp(z2)(rp(zi)< 綜上,若隨機預言機能計算出[qp(z)]2(z的噪聲遠小于p),則B就可以恢復p。接下來分析在隨機預言機模型下B成功的概率。 由步驟1可得,求解器B產生公鑰的分布與本文方案產生的正確分布相同,如文獻[8]所述:如果A猜測成功的可能性為ε,則敵方猜測成功的可能性至少為ε/2。如果固定p,在對應的公鑰pk下A猜測成功的可能性至少是ε/4,敵方猜測成功的可能性至少為ε/4。在子程序Learn-LSB(z,pk)的步驟4中,A猜測成功的可能性至少是ε/4-negl,對于該子程序而言,返回正確值的可能性很大,B有很大概率恢復出p。對于這樣的p,公鑰pk下的概率ε/4-negl也成立,則求解器B在運行中恢復p的概率至少是1/2(ε/4-negl),B重復調用算法(8/ε)ω(lbλ)次,此時B的時間復雜度是poly(λ,1/ε),因此,求解器B成功恢復p的概率至少是ε/2。至此,定理1證明完畢,本文方案是IND-CPA安全的。 網絡內部的攻擊者可以在數據聚合前后的2個階段獲得數據。從這2個方面進行如下分析: 1)在聚合前,內部攻擊者要獲得明文消息mi,在得到傳感器的加密私鑰p的同時,也要得到干擾因子πk。由于本文方案以簇為單位分配干擾因子,因此簇內每一個節點的干擾因子都相同。為獲知內部攻擊者是否會進行重復性攻擊,作如下證明:在一個簇內隨機選取一個節點的2個消息m1、m2,加密之后的密文為c1、c2。 (1) (2) 式(1)、式(2)相減并化簡可得: (3) 對于式(3),分2種情況討論: (1)m1-m2的值未知,則不能得到干擾因子πk。 (2)假設m1-m2的值已知,在N階乘法循環群內求解πk屬于離散對數困難問題,故也不能得到干擾因子πk。因此,πk的獲取是困難的。 由以上分析可得,本文方案可有效抵御來自網絡內部的攻擊。 表1所示為文獻[4,7,14]中的經典方案和本文方案的主要性能對比。其中,同態性指方案是否能實現全同態性。 表1 4種方案性能比較 由表1可以看出,與文獻[4]方案相比,本文方案無需可信第三方并且滿足全同態性;與文獻[7]方案相比,本文方案時間復雜度更低且能夠進行全同態運算;與文獻[14]方案相比,本文方案能夠抵御內部網絡攻擊。因此,與已有方案相比,本文方案在無需可信第三方的情況下,時間復雜度較低且滿足全同態性。 為改善WSN中的數據聚合效果,本文提出一種基于全同態加密的數據聚合方案,該方案具有如下優點:1)采用全同態加密方案,聚合器無需對密文解密就可以進行全同態運算;2)聚合器沒有解密密鑰,每個簇內的傳感器都有保密因子,并且不需要可信第三方來分配,因此,該方案既可以抵御內部攻擊也能節約存儲空間;3)以簇為單位分配保密干擾因子,將計算復雜度降低到O(1)。實驗結果驗證了該方案的性能優越性。下一步考慮改進公鑰產生算法并縮短公鑰的長度,以減少本文算法的運行時間,提高運算效率。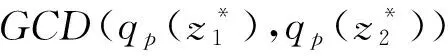
3.4 網絡內部攻擊分析
4 不同方案性能對比

5 結束語

