基于Lee模型與VOF方法的ACC基管內凝結性能的比較與數值模擬

楊婷婷， 楊景華

(華北電力大學 控制與計算機工程學院，北京 102206)

空冷凝汽器(ACC)由數十個空冷單元串并聯而成，由于空冷單元通過軸流風機驅動周圍環境空氣與翅片管直接換熱，節水效果顯著，ACC在我國缺水地區的燃煤機組上得到了大規模應用[1-3]，并成為我國西北沙漠地區迅速發展的太陽能光熱電站冷端系統的唯一選擇[4]。

在現行電廠空冷行業標準中，組成ACC的空冷單元是一臺由兩排60°對角布置的翅片管束與一臺軸流風機組成的“Λ”形凝結換熱器。空冷單元的翅片管束由上百根相同的翅片管并列而成，每根翅片管由基管和空冷翅片構成。在空冷機組上，根據基管管徑方向，即管內通流橫截面的幾何形狀，實際應用的ACC基管有大扁管、橢圓管和圓管3種。

翅片管是空冷機組冷端換熱的基本元器件，流經翅片管管內的蒸汽-液膜與管外冷卻空氣的換熱性能直接關系到空冷單元、ACC乃至整個空冷機組的熱耗和能耗性能指標。Kumar等[5-6]通過風洞實驗與數值模擬方法對流經管外翅片側流體的熱力學特性進行探討與分析，并在翅型設計上提出了提高空氣換熱性能的方法。相比翅片側取得的研究成果，對于管內氣-液兩相的熱力學特性的研究還較少，目前主要研究結果有：Owen等[7]利用理論分析結合計算流體力學(CFD)模擬，研究了汽輪機排汽母管進入雙排大扁管蒸汽的流動與分配規律；O'Donovan等[8]通過實驗研究了順流圓管內兩相流的流動性能與壓力損失；Berrichon等[9]通過實驗研究了逆流圓管內兩相流的液泛現象；Kekaula等[10]結合Nusselt理論與液池凝結模型，給出了順流圓管內液膜的流動換熱模型。

雖然以ACC基管內熱力學特性為研究對象的文獻較少，但目前在管內凝結換熱器應用的新興領域，如數據計算中心、航空電子和微管制冷等，已有大量基于CFD數值仿真的管內凝結性能、兩相交界面剪切力、管內流動壓降以及兩相流型特性的分析報道[11-13]出現，這些文獻的共同點在于：都是通過結合流體體積(VOF)方法[14]和Lee模型[15]，建立并求解管內凝結換熱的CFD算例。以上方法已被證明為除實驗外研究管內兩相流熱力學特性的主要方法。但在這些文獻中，很少有與ACC基管的管型、工作流體與邊界條件相同的研究內容出現。

筆者針對3種常用的ACC基管管型，基于VOF方法與Lee模型建立管內流體的控制方程，并考慮基管入口雷諾數Re和管壁過冷度(ΔTcool)對管內凝結換熱的影響，建立并求解CFD算例。通過設置3種管型管壁過冷度相等，使得管外空氣換熱的熱邊界條件保持一致，得出3種管型在不同傾角下換熱性能的數值對比結果；通過管內兩相流體積分數的可視化云圖，對基管內兩相流型進行定性，進而分析影響液膜厚度的管型與熱邊界因素。

1 研究對象

建模的工程管選取大扁管基管，這種基管在我國現階段典型600 MW空冷機組ACC上應用最為廣泛，其幾何尺寸見表1。

表1600MW機組ACC工程大扁管幾何尺寸

Tab.1GeometricparametersoftheACCflatbasetubeina600MWpowerplant

參數數值扁平幾何徑向高度w/mm200半橢圓幾何長軸a/mm15.2 半橢圓幾何短軸b/mm10 基管管長L/mm10 000 基管傾角β/(°)30基管徑向橫截面積A/mm21 120 基管徑向水力直徑Hd/mm40

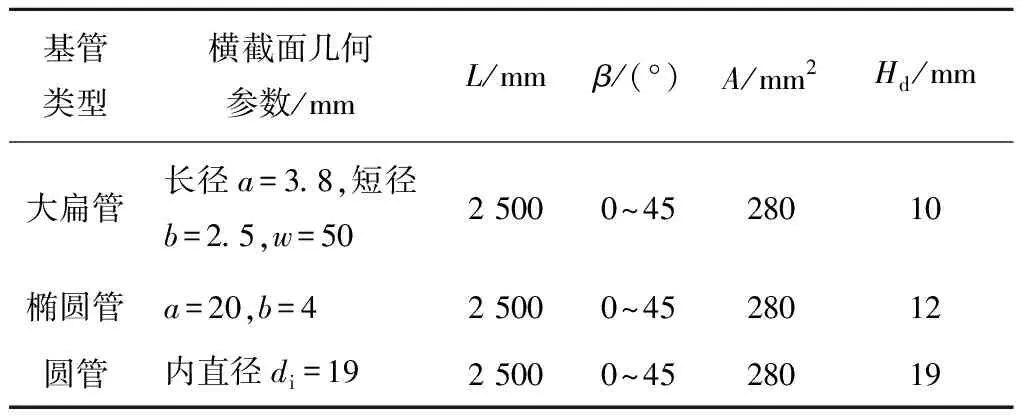
受限于CFD工作站的計算性能，筆者利用相似原理，在4∶1的縮小比例下[10]，對表1中的工程大扁管建立仿真樣管。并以大扁管樣管的橫截面積為基準，建立橢圓管和圓管的仿真樣管。CFD算例中的3種管型樣管的幾何尺寸見表2。

表2數值仿真的樣管幾何尺寸

Tab.2Geometricparametersadoptedinnumericalsimulation

基管類型橫截面幾何參數/mmL/mmβ/(°)A/mm2Hd/mm大扁管長徑a=3.8,短徑b=2.5,w=502 5000^4528010橢圓管a=20,b=42 5000^4528012圓管內直徑di=192 5000^4528019

2 數學模型及計算方法

2.1 數學模型

采用VOF方法分別對ACC基管內的兩相流體建立各相連續方程，并假設管內蒸汽在液膜表面傳熱傳質，只能在恒壓和準熱平衡狀態下進行，由此利用Lee模型計算得到相變質量，并以相變質量作為連續方程中的質量源項。

用單一方程形式建立氣-液兩相的動量與能量方程，由Lee模型計算得到相變質量，利用式(1)計算能量方程中的源項：

Q=hLV·SL

(1)

式中：Q為相變熱量；hLV為汽化潛熱；SL為凝結相變質量。

選用SSTk-ω方程描述ACC基管內兩相流的湍流特性，為加快湍流方程收斂，用以下公式估算ACC基管入口的湍流強度和湍流尺寸：

(2)

式中：I為湍流強度；l為湍流尺寸。

CFD計算中用到的控制方程均用Fluent軟件中的數學表達形式[16]表示(見表3)。其中，φ、ρ、κ、μ、Γ和ω分別為體積分數、密度、傳熱系數、黏度、湍能與耗散率的有效擴散量和耗散率；t、S、r、T、p、E、k、D、G和Y分別表示時間、連續方程源項、相變強度系數、溫度、壓力、能量、湍能、湍流方程的交叉項、速度梯度下的湍能或耗散率以及湍流下湍能與耗散率的耗散；u、g分別表示速度向量和重力向量；下標L、V、s和eff分別表示液相、氣相、飽和狀態和有效值。

表3 數值計算中用到的控制方程Tab.3 Governing equations used in numerical calculation

2.2 計算方法

2.2.1 網格模型

用Ansys ICEM 14.0 建立3種管型樣管的三維計算域模型，對徑向截面應用O型網格，網格在貼管壁區域加密，形成邊界層。計算域模型的邊界條件和網格邊界層放大圖如圖1所示。

圖1 3種ACC基管的計算網格Fig.1 Computational meshes for three types of ACC base tubes

2.2.2 邊界初始條件

樣管的入口邊界設置為速度入口，基于相似原理，需保證樣管與工程管在蒸汽入口的Re相同。先計算單根工程管在汽輪機熱耗率驗收(THA)工況下的入口蒸汽質量流率G，由U=G/ρin(U、ρin分別為蒸汽入口軸向流速和蒸汽入口密度)計算工程管蒸汽入口軸向流速，再將U放大4倍，得到樣管的蒸汽入口軸向流速。在工程管入口，蒸汽一般處于機組背壓ps對應下的飽和狀態，區分冬季與夏季，機組背壓在9～30 kPa之間變動，此處設置樣管入口熱屬性與工程管完全一致，即ps=9～30 kPa。

樣管的出口邊界設置為壓力出口，為防止數值算例出現逆流，將工作狀態下工程管出口的實際溫度、兩相體積分數及湍流等參數設置為CFD樣管的逆流參數。

一般來說，工作狀態下工程管的管壁溫度在位置分布上并不均等，為了比較3種管型的管內熱性能，設置樣管的管壁為等溫壁，將等溫壁的溫度定義為Twall，并將入口蒸汽飽和溫度Ts與Twall的溫差定義為CFD管壁過冷度，即ΔTcool=Ts-Twall。

CFD算例的邊界條件如表4所示。

表4 CFD算例的邊界條件Tab.4 Boundary conditions of CFD cases

2.2.3 數值計算方法

用Fluent軟件進行數值計算，在模擬樣管的凝結換熱時，使用穩態時間策略與隱式VOF方法，用QUICK算法重構相間界面，判斷收斂的標準為：能量方程迭代殘差小于10-6；樣管入口、出口質量差值小于10-4且連續方程殘差小于5×10-2時，連續方程收斂；其他控制方程的迭代殘差小于10-3。

在模擬樣管內流體的流型特性時，使用瞬態時間策略與顯式VOF方法，采用CICSAM算法重構相間界面，Courant數設定為0.25，采用變長時間步，初始時間步設為2×10-5s，每步的迭代次數為60次。

2.3 數學模型與數值方法驗證

2.3.1 網格無關性驗證

分別針對3種管型內兩相流，在計算邊界條件為G=14 kg/(m2·s)，Ts= 324 K，ΔTcool=2 K下， 設置Lee模型相變強度系數r=1 000 000 s-1，使用5種網格數量的網格，驗證數值結果對網格的獨立性，無關性指標為0.3～2.5 m凝結管段上管壁的平均熱流密度。通過無關性驗證，對大扁管、橢圓管與圓管的網格數量分別選定為5 950 800、5 200 000和5 678 400，在以上網格數量下，3種管型基管無關性指標偏差分別為0.98%、0.52%和0.40%，邊界層最小尺寸均為5 μm。

2.3.2 數學模型與數值方法有效性驗證

由于公開發表的、針對傾斜ACC基管負壓條件下凝結性能的實驗數據與經驗關聯式比較缺乏，筆者在3種管型垂直狀態下(β=0°)，設定Lee模型相變強度系數為r=400 000 s-1、800 000 s-1、1 000 000 s-1和1 200 000 s-1下，驗證數學模型與數值方法的有效性。

圖2給出了邊界條件為G=14 kg/(m2·s)，Ts=324 K，ps=13 kPa，ΔTcool=5 K，β=0°時，不同r值下，大扁管、橢圓管的管內局部凝結傳熱系數(HTC)數值解與Shah關聯式計算值[17]的對比。圖3是圓管在不同r值下，邊界條件為G=4.5 kg/(m2·s)，Ts=329 K，ps=17 kPa，ΔTcool=1.5 K，β=0°時，管內局部凝結HTC數值解與Al-Shammari實驗值[18]的對比。 由圖2和圖3可知，當r=1 000 000 s-1和1 200 000 s-1時，在大扁管、橢圓管以及圓管的中間段與出口段，數值解與Shah關聯式值和Al-Shammari實驗值吻合較好，誤差分別在25%、25%和15%，但是，在3種管型的入口段，數值解與Shah關聯式值和Al-Shammari實驗值之間出現了較大誤差，這是因為在基管入口區域，存在較大的管壁軸向熱傳導效應，使得管壁上液膜的厚度復雜多變，而數值計算中的VOF方法很難在入口段設置準確的液膜厚度初始值，與本文類似的入口段局部HTC偏差也出現在其他管內凝結數值模擬中[13,15,19]。

(b) 橢圓管

圖2 管內局部凝結HTC的Shah關聯式值與不同r值下數值解的對比

Fig.2 Comparison of HTC respectively calculated with Shah correlation and the method proposed under different values ofr

圖3 圓管內局部凝結HTC的Al-Shammari實驗值與不同r值下數值解的對比

Fig.3 Comparison of HTC between calculated data and Al-Shammari measurements under different values ofr

在比較r=1 000 000 s-1和1 200 000 s-1時兩相界面溫度與Ts的偏差后，發現前者偏差更小，最終本文CFD算例設置r=1 000 000 s-1。

3 結果與分析

3.1 管型與傾角對管內換熱的影響

圖4給出了3種管型邊界條件為G=14 kg/(m2·s)，Ts= 324 K，ps=13 kPa，ΔTcool=2 K，不同傾角下管內局部凝結HTC沿基管軸向的變化趨勢。由圖4(a)和圖4(c)可知，在β=0°和30°時，大扁管在全管段都表現出突出的局部換熱性能；由圖4(b)可知，在β=15°時，橢圓管在中間段和出口段表現出色；但由圖4(d)可知，在β=45°時，大扁管、橢圓管和圓管的局部凝結HTC波動均較大，很難比較3種管型的管內換熱性能。

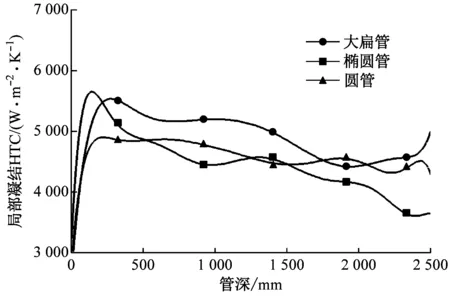
(a) β=0°

(b) β=15°

(c) β=30°

(d) β=45°圖4 3種管型管內局部凝結HTC的比較Fig.4 Comparison of local condensation HTC in three tubes

從圖4還可以看出，傾角在0°～45°內，β越大，管內局部凝結性能越好，管內局部凝結HTC沿軸向的波動越明顯。

為進一步在全管整體上比較不同傾角下異種管型的管內凝結性能，選用努塞爾數Nu作為ACC基管內換熱性能衡量指標，計算公式如下：

Nu=ho·Hd/κL

(3)

式中：ho、κL分別表示管內平均凝結HTC和液膜傳熱系數。

圖5給出了邊界條件為G=14 kg/(m2·s)，Ts=324 K，ps=13 kPa，ΔTcool=2 K時，3種管型在不同傾角下的平均凝結HTC和Nu。由圖5(a)可知，3種管型的平均凝結HTC相差不大，偏差在5%以內，相比之下，大扁管整體凝結性能較好。但由圖5(b)可知，3種管型的Nu相差明顯，圓管的Nu要超出大扁管與橢圓管2/3有余。造成這2種性能指標差別的原因是：由式(3)可知，Nu的計算不僅取決于管內平均凝結HTC，還與基管徑向水力直徑有關，在相同的徑向橫截面積A下，圓管Hd要遠大于大扁管和橢圓管(見表2)，因此，在ho差別不大的情況下，圓管獲得了較大的Nu。由圖5還可知，圓管在β=30°時的ho和Nu較其他傾角時更優，因此如不考慮除管內換熱性能外的其他指標，推薦β=30°的圓管為ACC的最優基管。

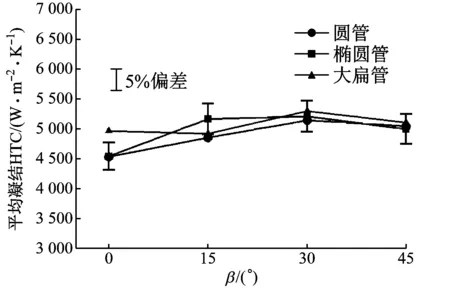
(a) 平均凝結HTC

(b) Nu圖5 3種管型在不同傾角下全管換熱性能的比較Fig.5 Comparison of overall heat-transfer performance for three tubes at different inclined angles

3.2 蒸汽入口Re對管內換熱的影響

為分析基管入口蒸汽熱力學特性對管內換熱的影響，引入蒸汽入口Re，其計算公式如下：

Re=ρin·U·Hd/μV

(4)

圖6(a)給出了ΔTcool=2 K，Ts= 324 K，ps=13 kPa，β=30°時，G=9 kg/(m2·s)、11 kg/(m2·s)、14 kg/(m2·s)和17 kg/(m2·s)時，3種管型的Nu隨Re的變化趨勢。圖6(b)給出了ΔTcool=2 K，G=14 kg/(m2·s)，β=30°時，Ts=316 K、324 K、333 K和342 K時，3種管型的Nu隨Re的變化趨勢。

(a) Re受入口蒸汽質量流率的影響

(b) Re受入口飽和溫度的影響圖6 3種管型在不同蒸汽入口Re下Nu的比較Fig.6 Comparison of Nusselt number under different Reynolds numbers of inlet steam for three ACC base tubes

由圖6(a)可知，蒸汽入口質量流率G的增大會加劇管內蒸汽凝結，觀察圖6(a)中3條曲線的斜率可知，圓管的管內換熱性能對G變化的敏感性較小。由圖6(b)可知，3種管型管內換熱性能對Ts變化的敏感性均較大，ACC基管的凝結性能隨蒸汽入口飽和溫度的減小而急劇下降，也就是說，當ACC入口蒸汽熱量保持不變的情況下，為維持空冷汽輪機的低背壓運行，軸流風機群必須提高風機轉速，從而付出比汽輪機高背壓時更高的軸流風機能耗成本。

3.3 管壁過冷度對管內換熱的影響

圖7給出了3種管型在G=17 kg/(m2·s)，Ts=324 K，ps=13 kPa，β=30°時，ΔTcool=2～8 K變化時Nu的變化趨勢。由圖7可知，對于橢圓管和大扁管，當 2 K≤ΔTcool≤6 K時，管壁過冷度的增大導致管內換熱性能輕微下降；對于圓管，當2 K≤ΔTcool<6 K時，管內性能隨管壁過冷度的增大而下降，當6 K≤ΔTcool≤8 K，管壁過冷度的增大會加劇管內蒸汽的凝結。

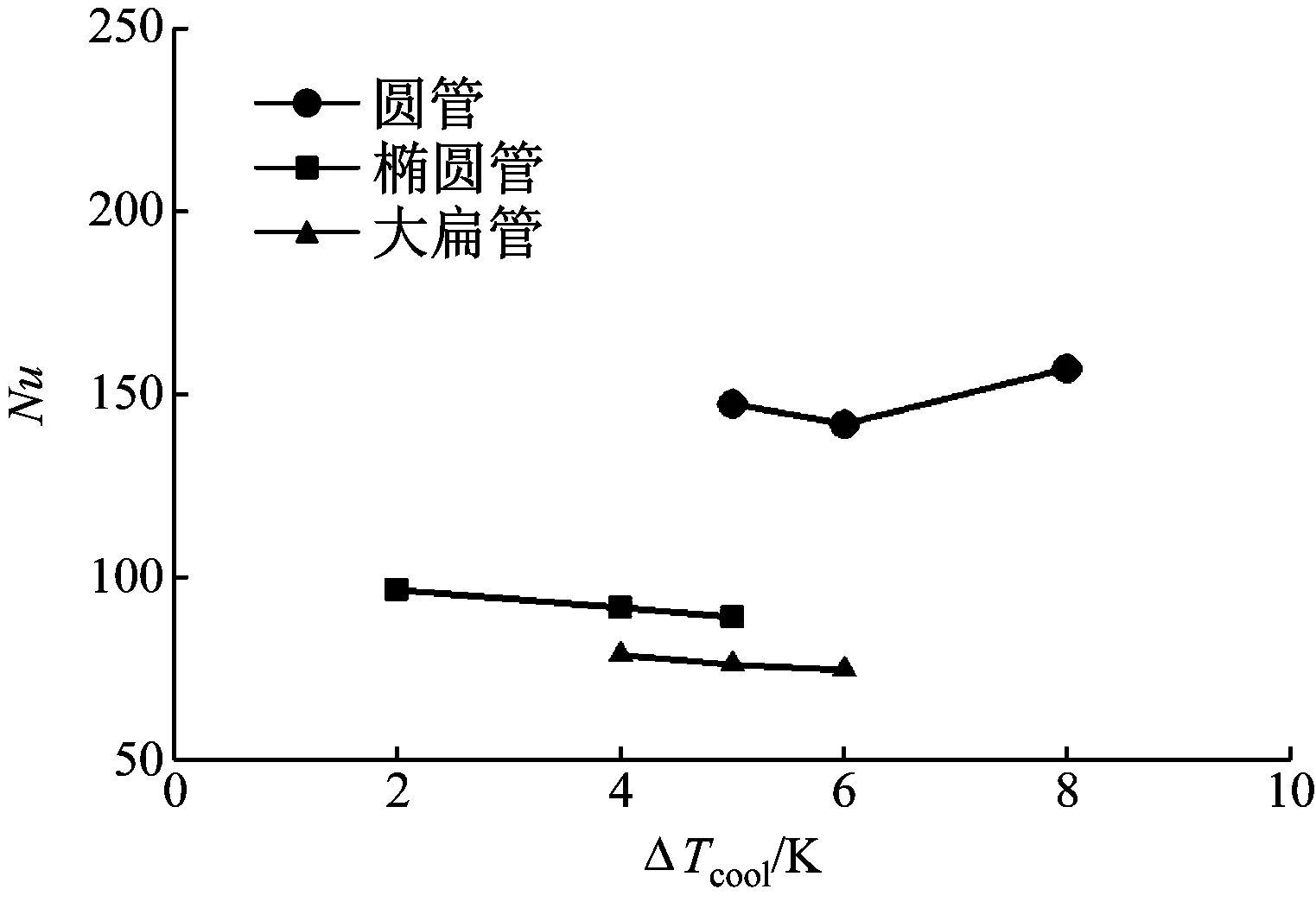
圖7 3種管型在不同管壁過冷度下的Nu對比Fig.7 Comparison of Nusselt number under different subcooling degree of wall for three ACC base tubes

3.4 蒸汽入口Re影響管內換熱的機理

對比圖5～圖7發現，3種管型的凝結性能受蒸汽入口Re的影響較大，由式(4)可知，蒸汽入口Re取決于蒸汽入口軸向流速和入口飽和溫度，因此對蒸汽入口軸向流速和入口飽和溫度對管內換熱的影響機理進行分析。

已有實驗與理論研究表明，氣-液交界面剪切力極大地加劇了管內蒸汽的凝結性能，而剪切力取決于氣-液交界面上的兩相流速度：

(5)

式中：y為氣-液交界面的法向方向；τ、u為剪切力向量和速度向量；下標I表示交界面。

由于管內兩相流的軸向速度遠大于橫向速度，且凝結液膜的厚度遠小于核心管的幾何尺寸，若忽略剪切力管徑向分量與液膜厚度，式(5)可簡化為：

(6)

由式(6)，并結合U與G關系式可知：G越大，U也越大，在其他邊界條件不變的情況下，管內兩相流交界面的剪切力也越大，由此導致管內蒸汽凝結加劇，這就是圖6(a)中G影響管內換熱性能的機理。

而入口飽和溫度對管內換熱的影響機理，可通過Lee模型來解釋。Lee模型中描述蒸汽相變質量的表達式如下：

(7)

由蒸汽熱力學屬性關聯式REFPROP 9.0[19]計算ρin，可知ρin的取值取決于其飽和溫度Ts。在圖6(b)中，蒸汽入口飽和溫度Ts由316 K升高到324 K，ρV從0.054 kg/m3增大到0.18 kg/m3，幾乎放大了1個數量級。式(7)中，ρV的數量級增大使得計算網格內相變質量S急劇增大，聯立式(1)和式(7)，S的增大導致計算單元釋放相變熱量Q同步增大。兩相流凝結HTC的計算式為：

h=Q/(Acell·ΔTcool)

(8)

式中：Acell為管壁網格單元的面積。

由式(8)可知，在網格模型和熱邊界條件不變的情況下，相變熱量Q的增大會提高管內兩相流凝結HTC。

3.5 3種ACC基管內兩相流的流動特征

圖8給出了3種管型在出口處兩相流體積分數云圖與其局部放大特征。由圖8可知，在3種管型的出口處，基管傾斜布置下，重力徑向分量對液膜的作用力導致基管底部有凝結水累積出現：對于大扁管和橢圓管來說，累積輕微；而在圓管內累積較明顯。通過觀察局部云圖展示的液膜特征可以發現：在3種管型的管壁上，液相沿管壁呈厚度很薄的膜狀分布，且表面光滑。也就是說，凝結水在基管管壁上作光滑無波紋的膜狀流動。由于圖8展示的液膜流動特征，與Oshinowo-Charles 流型圖的降落膜狀流[20]高度吻合，將3種ACC基管內兩相流的流型歸類為降落膜狀流。

此外，對比局部云圖中3種管型的液膜厚度發現，圓管內的液膜厚度要遠大于大扁管和橢圓管，這也是在圓管的底部，凝結水累積現象更為明顯所致。除了管型對管內液膜特征的影響之外，由圖8還可知，3種管型中，圓管的G最小，ΔTcool最大。因此，基管內液膜的厚度與底部累積不但與管型有關，還取決于基管入口的G和ΔTcool：即基管入口的蒸汽質量流率越小，管壁溫度越低，管內的凝結水液膜越厚，基管底部的凝結水累積現象也越明顯。

4 結 論

(1) 在3種管型的徑向橫截面積與傾角相同的條件下，圓管內的兩相流凝結換熱Nu超過大扁管和橢圓管近1倍；而同一基管在不同傾角下的Nu對比結果表明，當傾角為30°時，ACC基管的凝結換熱性能最佳。當ACC基管的選型只考慮管內換熱性能的前提下，建議優先選擇傾角30°的圓管。

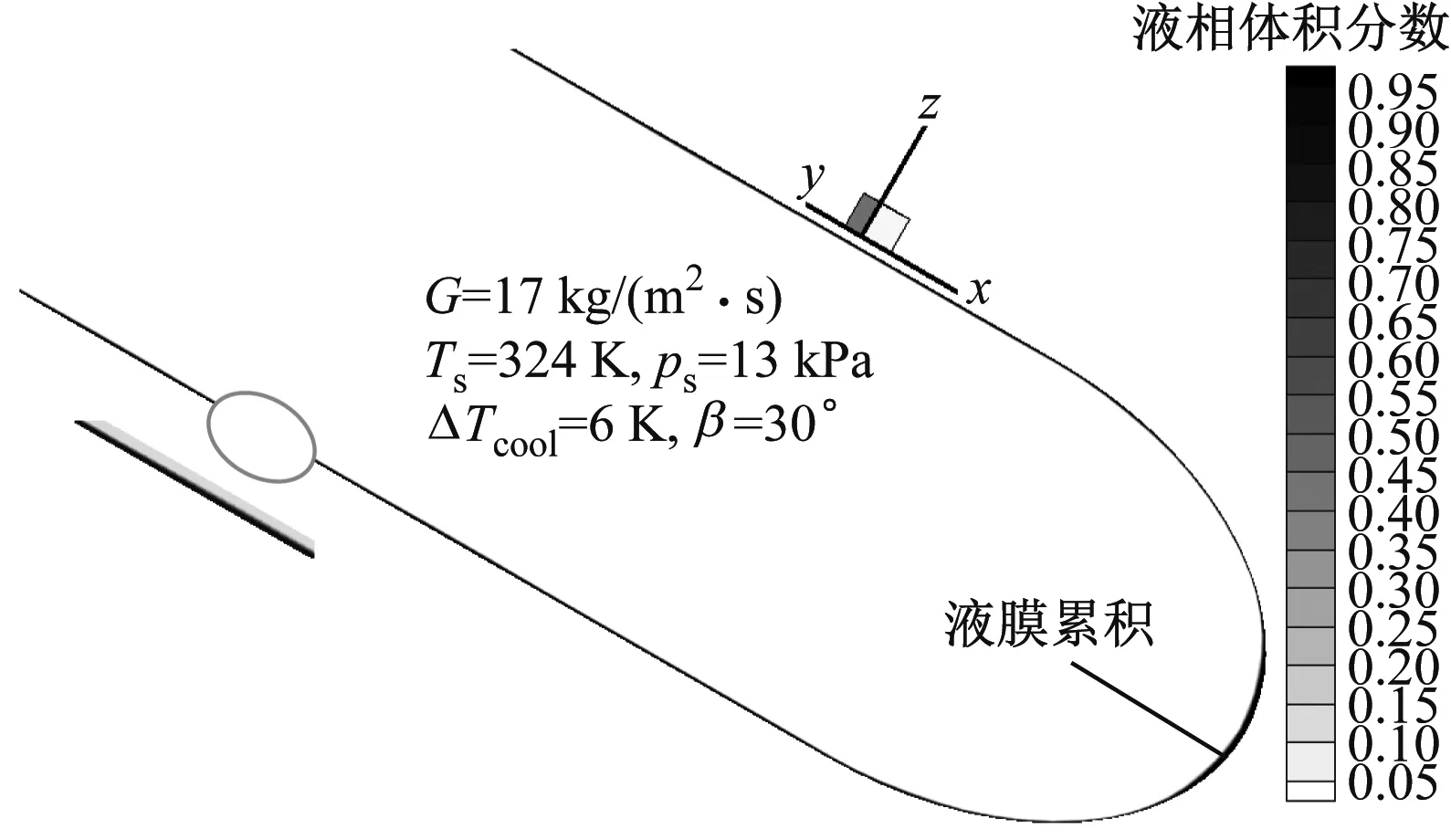
(a) 大扁管

(b) 橢圓管

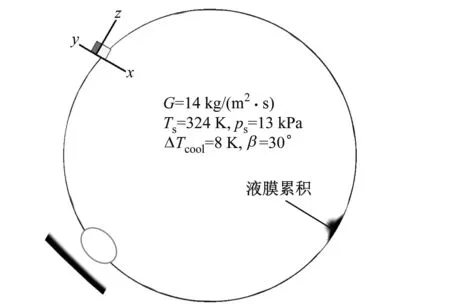
(c) 圓管圖8 3種管型內兩相流在出口處的流型比較Fig.8 Comparison of two-phase flow pattern at outlet of three ACC base tubes

(2) ACC基管入口Re隨基管入口飽和溫度的升高和蒸汽入口軸向流速的增加而增大，而Re的增大會提高基管的換熱Nu，從而加劇蒸汽在管內的凝結。

(3) 當管壁過冷度增大時，大扁管和橢圓管的Nu會輕微降低；而圓管的換熱性能在2 K≤ΔTcool<6 K時，隨管壁過冷度的增大而降低，當6 K≤ΔTcool≤8 K時，管壁過冷度的增大會加強管內蒸汽的凝結。

(4) 3種管型的兩相流型都可歸類為表面光滑的降落膜狀流；3種管型中，圓管內的凝結液膜厚度最大，除管型外，ACC基管內的液膜厚度還受蒸汽入口流速和管壁過冷度的影響。

(5) 在本文全部算例中，3種管型的管內平均凝結HTC在4 000～7 000 W/(m2·K)內浮動，而管外翅片側冷卻空氣的平均HTC一般小于100 W/(m2·K)，管內外工作流體的換熱性能相差2個數量級。因此，在ACC基管的選型與優化中，除核心管的管型因素外，工作重點應在空冷翅片的選型與設計優化上。