陀螺進動中的“角動量不守恒”問題

邵懷華 卓玉霖

(六盤水師范學院電氣工程學院，貴州 六盤水 553000)

在回轉效應演示實驗中，為了突出進動這一“反抗”重力的神奇力學現象，往往通過給陀螺儀一個較大的自轉角動量等方式減小其章動，但是這樣會產生豎直方向的進動角動量從何而來的疑問。圖1所示為回轉效應演示儀簡化模型，L為自轉角動量，R為回轉半徑，O為支點。為了討論方便，假設陀螺質量為m，質心在懸空端P點。

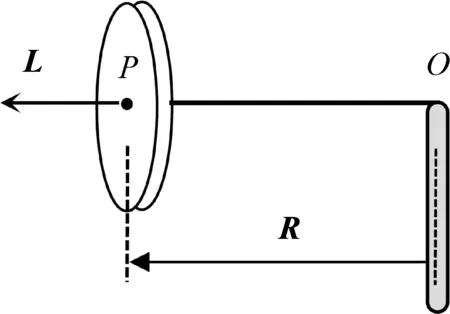
圖1 回轉效應演示儀簡化模型示意圖

均勻進動時，由力學基本知識可知

(1)

1 陀螺動力學分析

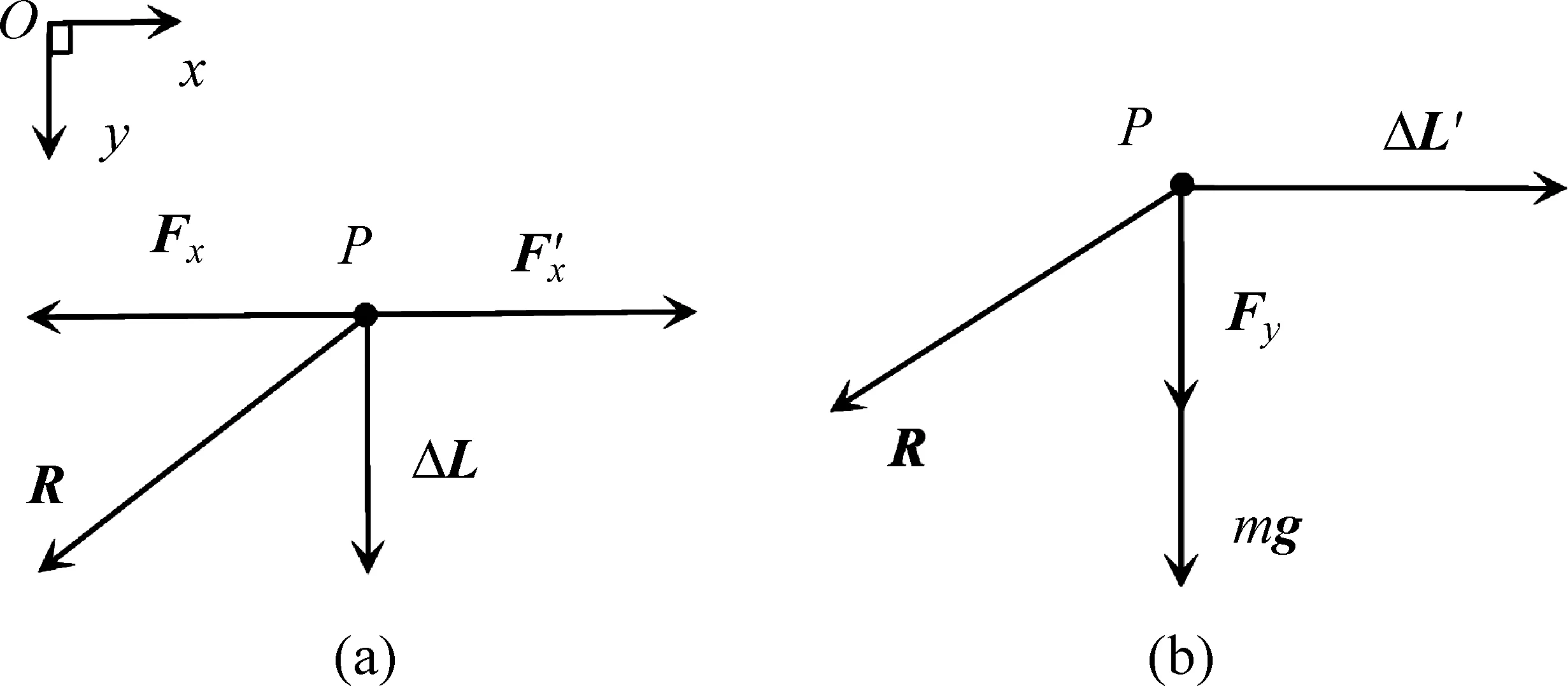
圖2 陀螺轉動的矢量分析圖(a) 縱向轉動; (b) 橫向轉動

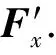
令ωp和ωn分別表示進動和章動角速度的大小。分析圖2(a)，可得如下方程組

(2)

式中ax表示陀螺在慣性力作用下水平運動加速度的大小。上式可解得關于ωp和ωn的微分方程

(3)

同樣，分析圖2(b)可得

(4)

解得

(5)

聯立式(3)、式(5)，結合初始條件ωp(0)=0,ωn(0)=0可得進動和章動角速度大小隨時間的變化關系

(6)

進而對兩個角速度分別求積分，可以得到進動角θ和章動角α隨時間的變化關系，結合初始條件θ(0)=0,α(0)=0可得

(7)

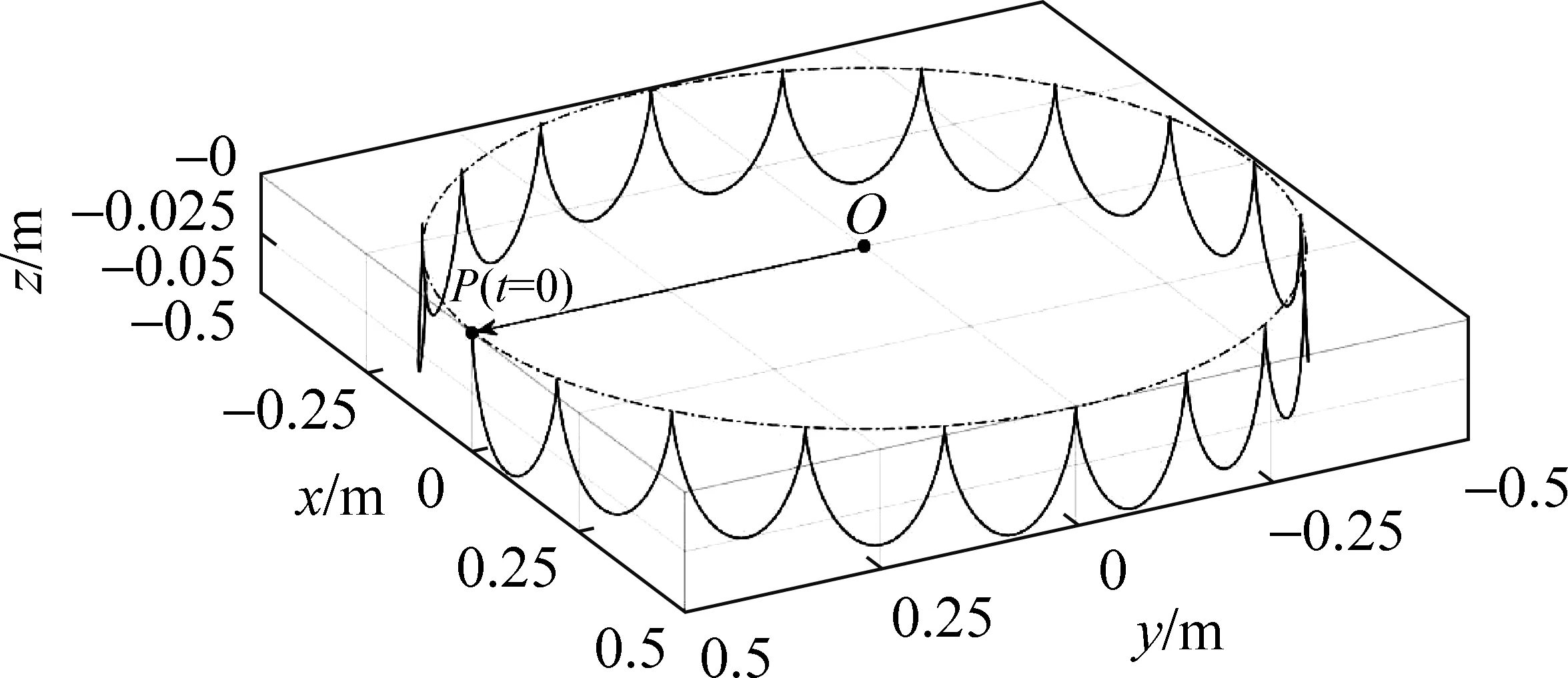
圖3 理想情況下陀螺儀懸空端P的空間軌跡

此即理想情況下，關于回轉儀懸空端P運動行為的一個較為精確的解。圖3是對理想情況下回轉儀懸空端P軌跡的數值模擬結果。可以看出水平釋放后陀螺并不是做穩定的進動，而是以其進動角速度和章動角速度均周期性振蕩變化的規律“抖動”前進。

但在實際情況中，由于摩擦的存在，式(6)、式(7)中的振蕩項將很快衰減為零。去除振蕩項之后的穩定值為

(8)

下面對此做出證明：

在章動很小的情況下，

(9)

穩定進動角動量的大小為

(10)

可見二者大小相等，但方向相反。

因此，實際情況應該是這樣的，水平釋放后陀螺開始抖動著前進，穩定后其懸空端會稍微向下傾斜，使自轉角動量L有一個向下的分量抵消了進動角動量，從而保證了豎直方向角動量守恒。

2 阻尼條件下的動力學分析

為了弄清實際陀螺進動從開始到穩定的過程，我們考慮有阻尼的情況，其主要來自于陀螺轉動時與支架的摩擦。類似于運動物體在空氣中運動受到的阻力在速率不高時為f=-k，k為阻力系數，轉動中摩擦產生阻尼力矩，大小與角速度成正比，方向相反。即，Mr=-krω；kr為轉動阻尼系數。然而，一般情況下進動阻尼遠小于章動阻尼。忽略進動阻尼，只考慮章動阻尼后，式(2)、式(3)保持不變，但式(4)改寫為

(4a)

式中kn為章動阻尼系數。化簡可得

(5a)

同樣，上式聯立式(3)，結合初始條件可得有章動阻尼時的進動角速度ωp和章動角速度ωn的大小

(11)

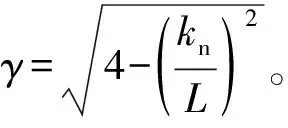
這即是引入章動阻尼時，關于陀螺運動的一個較為精確的解。圖4是考慮章動阻尼時P點空間軌跡的數值模擬結果。如圖4所示，為保證系統豎直方向的角動量守恒(恒為零)，從水平位置P(t=0)釋放后陀螺開始抖動著進動，穩定后其懸空端會稍微向下傾斜至P′，使其自轉角動量L有一個向下的分量正好抵消進動角動量。

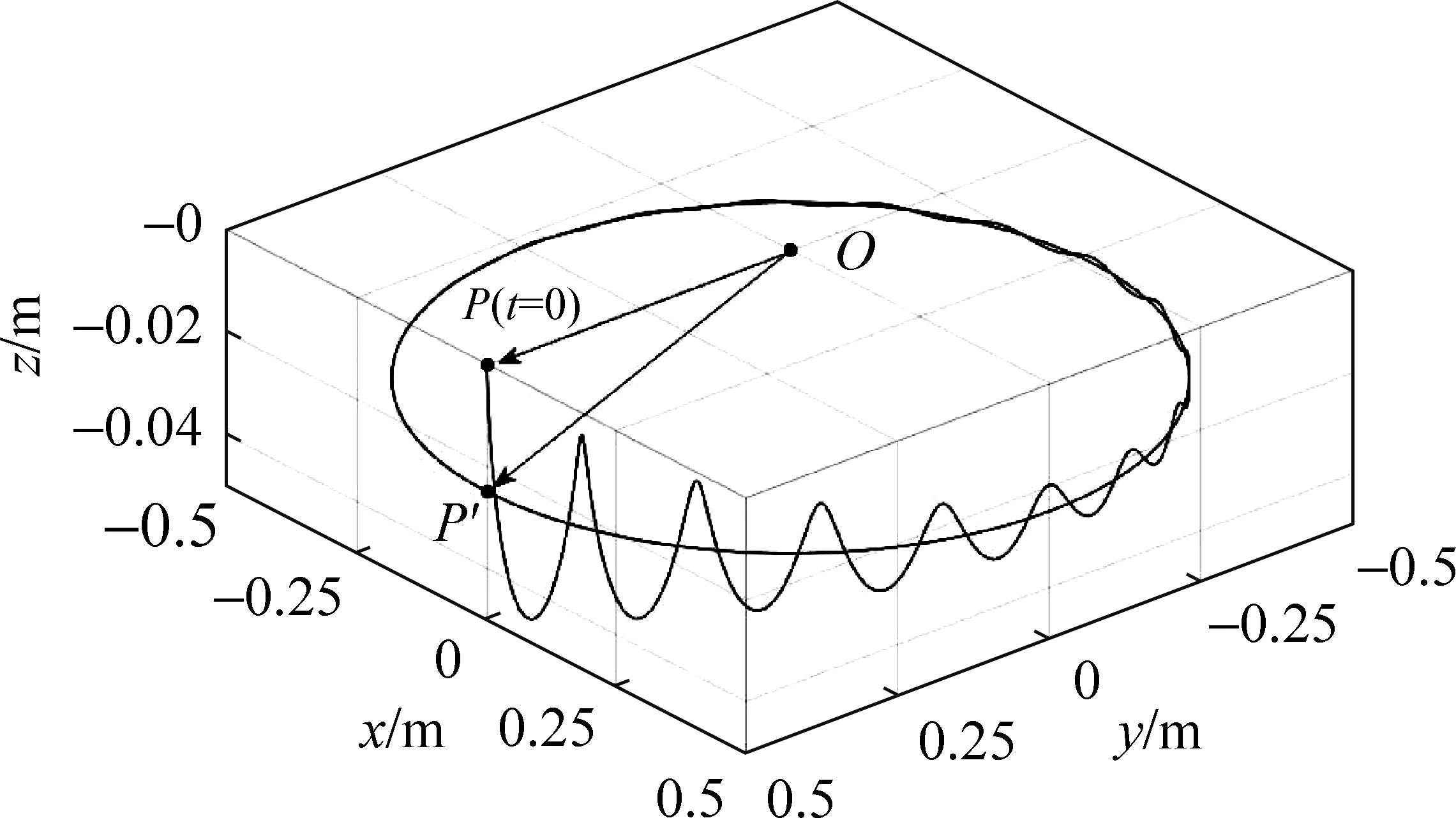
圖4 章動阻尼下陀螺儀懸空端P點空間軌跡

3 全阻尼情況討論

實際上摩擦也會產生進動阻尼，并且進動阻尼力矩沿豎直方向，使系統在豎直方向受到的合力矩不再為零，該方向的角動量也不再守恒。我們也對全阻尼情況作了計算，此時進動角θ隨時間的變化關系為

(14)

式中kn,kp分別為章動和進動阻尼系數。章動角α隨時間的變化關系

(15)

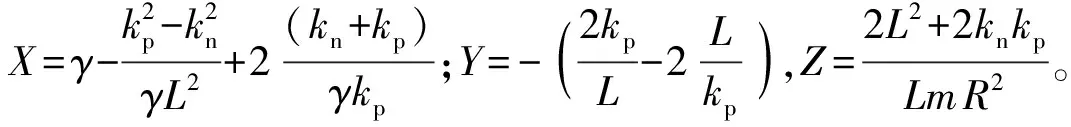
圖5所示為全阻尼下陀螺儀懸空端P的軌跡的數值模擬結果。可以看出，摩擦逐漸消耗系統的能量，陀螺最終會“屈服”于重力，慢慢掉下去。只是一般演示實驗中，由于重力力矩遠大于阻尼力矩，幾個進動周期內陀螺下落不明顯。

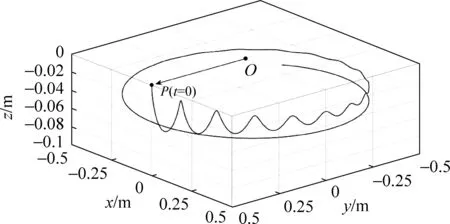
圖5 全阻尼情況下陀螺儀懸空端P的空間軌跡

4 結語

本文通過解析計算和數值模擬，系統研究了回轉效應中的陀螺運動規律。首先考慮理想情況，發現水平釋放后陀螺并不是作穩定的進動，而是以進動和章動角速度均周期性變化的規律“抖動”前進。實際情況，由于摩擦，抖動會逐漸消失，穩定后陀螺下傾，使自轉角動量有一個向下的分量抵消了進動角動量，從而保證了豎直方向角動量恒為零，解釋了進動演示實驗中由于進動角動量出現導致的看似豎直方向上的角動量“不守恒”問題。進而為了弄清陀螺從水平釋放達到穩定的動力學過程，我們逐步在模型中引入章動和進動阻尼，并詳細分析了陀螺在阻尼條件下的運動行為。