不同照明條件下全息圖的衍射場分析
丁文革 楊晨鶴 代秀紅 張榮香
(河北大學物理科學與技術學院,河北 保定 071002)
光波經過光學系統后形成的波場,一般是比較復雜的。現代光學的思想就是要在復雜的波場中分離出簡單的波動成分:平面波和球面波。由于波場的主要特征體現在波前函數的相因子中,因此可以根據波前函數的相因子來判斷波場的性質,分析衍射場的主要特征,這就是所謂的波前相因子判斷法[1,2]。在2015 全國高等院校光學教學暨學術研討會上,北京大學鐘錫華教授曾積極倡導采用波前相因子判斷法分析復雜波場的主要成分[3]。實際上在很多場合,只需掌握衍射場的主要特征就夠用了,在全息技術中就是如此。
全息技術是利用干涉和衍射原理記錄并再現物體的真實三維圖像技術,現在已經廣泛應用于不同的領域[4-6]。但是在一般光學教材中介紹全息再現時,總是說“用一束同參考光的波長和傳播方向完全相同的光束照射全息圖,就可以還原出物體的樣子”[7-9]。 那么,如果采用與參考光波不同的照明光波,結果如何呢?這里將采用波前相因子判斷法,對不同照明條件下全息圖的復雜衍射場進行詳細解析,識別出再現波場中與物光波相關的信息,并用圖示法把再現圖像的分布情況表示出來。這不僅有助于我們深入理解全息再現圖像的特點并應用于不同的實際需求中,而且有助于我們以后更好地利用波前相因子判斷法,處理復雜波場問題。
1 理論基礎
φ(x,y)=k(sinθ1x+sinθ2y)
(1)
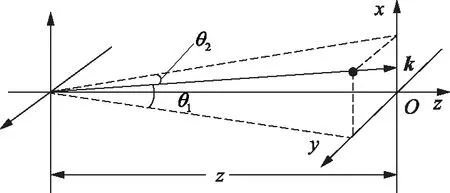
圖1 沿方向角(θ1,θ2)傳播的平面波
在傍軸近似下,中心在(x0,y0,-z0)的發散球面波和中心在(x0,y0,z0)的會聚球面波,在z=0波前平面上的相位分布φ+(x,y)和φ-(x,y)分別為[1]
(2)
式(1)和式(2)中,k=2π/λ表示波矢的大小。
2 全息記錄與再現
如圖2所示,一束正入射的單色平面參考光波,與一束球面物光波相干疊加,在z=0平面上形成干涉條紋。將記錄介質放在該平面位置進行曝光,把干涉條紋拍攝下來,然后進行線性沖洗,即得到一張全息圖。參考光波在z=0平面上的復振幅分布(即波前函數)為
(3)
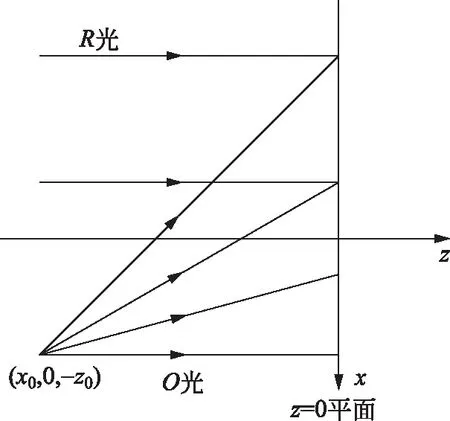
圖2 全息記錄
在傍軸近似下,中心在(x0,0,-z0)的球面物光波的波前函數為
(4)
為方便計算,已設eikz0=1。二者相干疊加形成的干涉場強度分布為
(5)
(6)
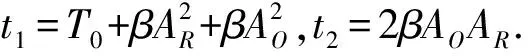
(7)
該衍射場一般是很復雜的。下面我們采用波前相因子判斷法,就幾種不同照明光波情形,詳細分析全息圖衍射場中物光波前的再現情況。
3 不同平面光波照明時全息圖的衍射場分析
3.1 改變入射光波長
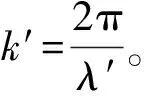
(8)
這與全息記錄時參考光的波前函數相同。將上式代入式(7),并整理可將全息圖的衍射場解析為
(9)
顯然上式第一項只包含照明光波的信息,稱之為0級衍射波。與式(4)中物光波的相因子比較可見,式(9)中第二項和第三項分別包含了物光波前及物光共軛波前,稱之為+1級衍射波和-1級衍射波。由于照明光的波長與記錄參考光的波長不等,即λ′≠λ,此時分析全息圖的衍射場時,要以λ′為標準進行波前函數各項相因子的分析。為方便計,設
(10)
則+1級衍射波和-1級衍射波的相位分布φ+(x,y)和φ-(x,y)可改寫為
(11)
可見,+1級衍射波為中心位于(x0,0,-z1)的一列發散球面波,-1級衍射波為中心位于(x0,0,z1)的一列會聚球面波,橫向放大率V+=V-=1。即在全息圖左側成一等大的虛像,虛像位置相對于原記錄物點有一個縱向的位移,在全息圖右側對稱位置處成一等大的實像,如圖3所示。這一特點使得我們可以采用不同波長的光,如紅外光、紫外光甚至X射線記錄全息圖,而用可見光照射再現物光波前。
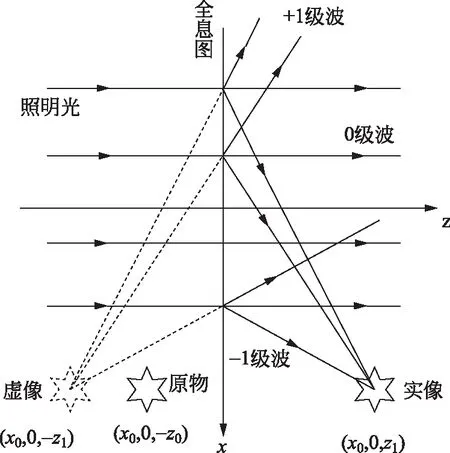
圖3 改變照明正入射平面波波長時的成像圖
3.2 改變入射光波的方向
如圖4所示,當平面光波以θ角照明全息圖時,其波前函數為
(12)
將上式代入式(7),并整理可將全息圖的衍射場解析為
(13)
經整理,上式中第二項+1級衍射波和第三項-1級衍射波的相位分布φ+(x,y)和φ-(x,y)可表示為
(14)
其中,C1是與波前場點無關的常數。可見,+1級衍射波為中心位于[(x0-z0sinθ),0,-z0]的一列發散球面波,-1級衍射波為中心位于[(x0-z0sinθ),0,z0]的一列會聚球面波。即在全息圖左側成一虛像,虛像位置相對于原記錄物點有一個橫向的位移,在全息圖右側對稱位置處成一實像。由于橫向位移Δx=(x0-z0sinθ)-x0=-z0sinθ,與x0無關,所以橫向放大率V+=V-=1,即所成虛像和實像與原物大小相等。如圖4所示。這一特點使得我們可以通過改變照明光的傳播方向,而實現再現像位置的調整。

圖4 斜入射平面波照明時的成像圖
4 不同球面光波照明時全息圖的衍射場分析
4.1 發散球面波作為照明光波
設照明光波為中心在(0,0,-z′)的發散球面波,滿足傍軸條件時,此球面波的波前函數為
(15)
為方便計,我們已設exp(ikz′)=1。將上式代入式(7),并整理可將全息圖的衍射場解析為
(16)
顯然,上式中第一項的相因子與照明光波相同。下面我們主要對式中第二項+1級衍射波和第三項-1級衍射波的相因子加以分析。設+1級衍射波的相位分布為φ+(x,y),經推導可得
(17)
其中,C2是與波前場點無關的常數;z2滿足下式
(18)

設-1級衍射波的相位分布為φ-(x,y),經推導可得
(19)
其中,C3為與波前平面上場點無關的常數;z3滿足下式
(20)
(21)
考慮到z0與z′的大小關系,其成像可以分為以下兩種情況:
(1) 當z0>z′時,根據式(20),有z3<0,則-1級衍射波為一列發散的球面波,即在全息圖左側形成一個虛像。由于|z3|可以大于、等于或小于z0,從而|V-|可以有大于、等于或小于1共3種不同的情況。即該虛像與原物體相比可能放大、可能縮小、亦可能等大。成放大虛像的情形如圖5(a)所示。
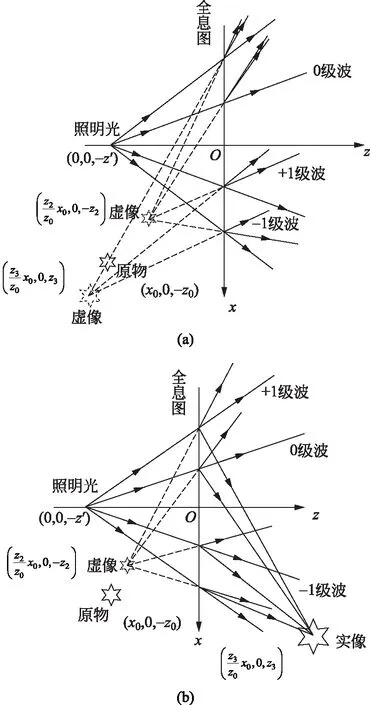
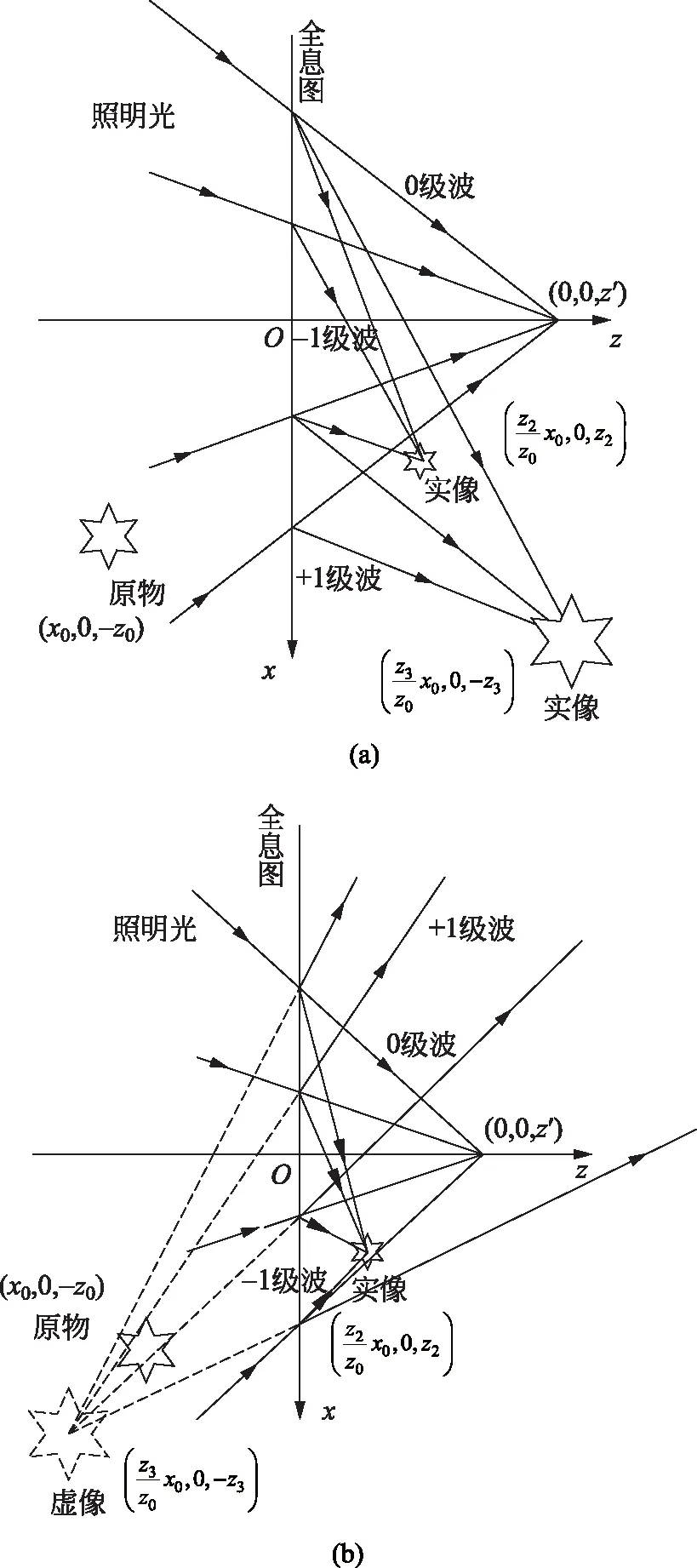
圖5 發散球面波照明的全息圖(a) z0>z′; (b) z0 (2) 當z0 設照明光波為中心在(0,0,z′)的會聚球面波,滿足傍軸條件時,此球面波的波前函數為 (22) 為方便計,我們已設exp(-ikz′)=1。將上式代入式(7),并整理可將全息圖的衍射場解析為 (23) (1) 當z0>z′時,有z3<0,+1級衍射波為一列會聚的球面波。在全息圖右側形成一個實像。由于|z3|可以大于、等于或小于z0,從而|V+|可以有大于、等于或小于1共3種不同的情況。即該實像與原物相比可能放大、可能縮小、亦可能等大。成放大實像的情形如圖6(a)所示。 圖6 會聚球面波照明的全息圖(a) z0>z′; (b) z0 (2) 當z0 我們采用波前相因子判斷法對不同照明條件下全息圖的衍射場進行了詳細分析。結果表明,采用單色平面光波照明全息圖時,所成虛像和實像關于全息圖對稱,且與原物大小相同。改變入射光的波長或傳播方向,成像位置會有相應改變。采用單色球面光波照明全息圖時,所成的兩個像關于全息圖不對稱,且所成像的橫向放大率存在大于、小于和等于1共3種可能性。全息成像的這些特點,在應用中具有實際意義。比如采用不同波長的光,如紅外光、紫外光甚至X射線記錄的全息圖,均可以用可見光照射而再現物光波前;采用球面波照明全息圖時可以將所成像進行放大或縮小;通過調整相應參量,可以實現成像位置的調整,等等。4.2 會聚球面波作為照明光波
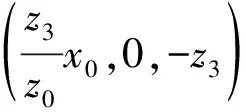
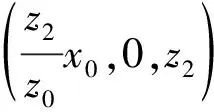
5 結論

