新高考選考科目計分問題與政策調適

王 森

（華東師范大學教育學部/國家教育宏觀政策研究院，上海200062）

一、新高考計分政策

為實現不同選考科目之間的可比性，新高考多數試點采用固定比例法劃定等級。其潛在理論假設為“考生的排名位置反映了其能力水平”。在新高考選考科目尚缺乏測驗等級標準的現狀下，該方法較為高效地解決了等級分數線劃定問題。

出于分數合成的需要，新高考多數試點采用“等級賦分”的分數報告形式，主要有“直接賦分”與“公式轉換賦分”兩種。“直接賦分”即根據事先公布的比例確定等級，直接賦予考生所在等級對應的分數，上海[1]、浙江[2]、北京[3][4]、天津[5]均采用該賦分方法。“公式轉換賦分”是山東試點使用的賦分方法，即根據“等比例轉換法則”，分別轉換到各個賦分區間進行賦分。將每門等級考試科目考生的原始成績從高到低劃分為八個等級。參照正態分布原則，確定各等級人數所占比例。等級考試科目成績計入考生總成績時，將考生原始成績依照等比例轉換法則，分別轉換到八個分數區間，得到考生的等級成績。[6]

受考生異質性影響，固定比例法劃定等級無法準確測量考生實際學業水平，不同科目的考生即使有相同的等級分數，也無法判斷實際的學業水平的高下。[7]當前多數試點試圖通過增加等級數量（將5等細化為21級）避免考生賦分誤差。在實踐過程中，很有可能出現“原始分差1分，等級轉換分差3分甚至6分”的現象，由此引發的“分分計較”問題備受關注。有研究認為等級數量的劃分與考試的功能有關。[8]選考科目多等級設置并賦分的方法在一定程度上模糊了考生之間的差異，與考試的選拔功能之間出現了矛盾。

多科分數合成方法的選取通常受多種因素制約，既有技術因素，也有社會因素。[9]等級賦分試圖滿足高校“總分錄取”招生的需求。然而，教育測量理論一般認為，科目之間的分數合成必須同時滿足“參照點”與“單位”相同兩個條件。當前試點地區的統考科目普遍采用原始分報告（除海南外），而選考科目則使用等級轉換后賦分的分數報告方式。兩類分數報告方式不同，其參照點和單位也不一致。新高考選考科目等級轉換分數與統考科目原始分采用直接相加的分數合成方式，其科學性值得反思。

二、滬浙首批試點計分政策調整

（一）選考科目保障機制

首批試點計分政策調整主要是針對新高考“物理等科目選考人數下降”的問題。為解決這一問題，浙江和上海先后出臺了“選考科目保障機制”，即“當選考某科目某次考試賦分人數少于保障數量時，以保障數量為基數進行等級賦分，保障數量按國家相關學科人才培養需求確定”[10][11]。

以浙江選考物理6.5萬人保障基數為例，按照等級賦分規則，根據考生選考物理的人數不同，會出現三種情況。其一，如果有8萬名考生選考物理（大于6.5萬人），則有800位考生的成績為滿分；其二，如果有6.5萬名考生選考物理，則有650位考生的成績為滿分；其三，如果有1萬名考生選考物理（小于6.5萬人），保障機制發揮作用，按照6.5萬人的基數進行賦分，有650位考生的成績為滿分。“保障基數”政策的出臺，旨在從政策層面維護選考物理等科目的考生的利益，平衡了“選考”與“計分”之間的關系，將可能發生的“考生群體變化”對計分科學性的影響降到較低水平。

（二）考生選考對計分政策的影響

選考科目之間“考生的能力水平大體相當”是“等級賦分”實現不同選考科目可比的重要前提。“選考科目保障機制”能夠大致將某一選考科目的選考人數維持在合理的區間內，并不能保證各選考科目考生的總體分布相似。以浙江選考物理科目為例進行極端情況假設，排序為最后一位考生的原始成績即使為85分（滿分100分），經過“等級賦分”后，計入高考總成績的實際分數也僅為40分。

根據“高校要求和自身特長”的選考是“等級賦分”計分政策設計的依據之一。[12]基于現行招生錄取政策中“分數最大化”的導向，考生并不能完全根據“高校要求和自身特長”來自主選擇考試科目。水平相近的考生集中選考某一科目，出現了多數能力水平處于中等及以下的考生集體“規避”物理科目的現象，致使選考科目之間的可比性降低。

高校對選考科目的要求則可能引發連鎖反應。基于“報考生源”“考生總分”“學校社會聲譽”“高校之間的競爭”等多方面因素的考慮，多數專業沒有提出較高的選考要求。高校一旦對選考科目提出過高要求，就會導致考生總分相較于不限定選考科目的同類高校大幅度降低，給社會公眾帶來的直觀感受是錄取標準的降低。這將對高校的社會聲譽產生不良影響，對其未來的生源質量造成不可估量的損失。以各科成績的總分作為高校錄取的依據，從高到低進行排序。等級劃定后進行賦分，服務于高校錄取“總分”的需要。在總分大排序、選考只需一科符合、院校專業組錄取的機制下，選考科目的設定實效有限。[13]“總分錄取”招生模式會導致多數高校缺乏制定選考科目的動力，影響考生的選考行為，進而使得固定比例劃分等級的前提無法得到較好的滿足。

（三）計分政策對物理選考人數下降問題的影響

物理選考人數下降的問題不能簡單歸結為計分政策。物理等科學科目組合的選考人數下降，在實施多學科選考政策的其他國家或地區也有類似情況發生。如英國A-level考試盡管具備較為成熟與完善的計分方式，但依然不可避免科學科目選考人數下降的事實。[14]在科學科目選考人數下滑的全球背景下，如何提升考生的選考意愿是各國政府面臨的普遍問題。

在我國高考的實踐中，2006年廣東高考選考科目中的物理等科學科目報考人數已出現下降趨勢。[15]廣東出現了以下現象：“由于考生選擇的X科科目不同，每個X科的考生人數不一，報考人數越多的科目，考生越容易獲得較高的標準分。由此導致幾年內廣東報考物理的考生由10多萬人迅速降至五六萬人，很多考生被迫棄理從文，或選擇試題難度低的科目。”[16]然而，在江蘇2008年高考改革方案的選考科目設計中，物理等科學科目選考人數較為平穩。這與其“理科必選物理，文科必選歷史”的科目設置政策密切相關。因此，在新高考中，計分政策是“物理選考人數下降”的影響因素之一，但不是唯一因素。

三、考試可比性理論與實踐

（一）考試可比性理論

考試可比性包括不同考試機構測量結果之間的比較、相同科目不同選修課程之間的比較、相同選修課程不同選修模塊之間的比較、不同科目之間的比較、不同年度之間的比較等，按復雜程度由低到高，可以劃分為三種情形。[17]一是“并行版本”（parallel versions），即在同一考試科目中多次測驗之間的比較。二是“非并行版本”（non-parallel versions），即不同考試科目使用相同的標準。這意味著它們在某種程度上代表了同一教育水平的成就，高校通過對考生的成績進行等效處理，以方便錄取。要使兩個測試等效，它們必須（至少）建立在相同的內容和統計框架之上。三是“多重非并行版本”（multiple non-parallel versions），需要實現不同考試大綱、不同科目、不同年度、不同考試機構之間測量結果等的可比性。

有關考試可比性的定義，學界并不統一。比較有代表性的定義如下：可以比較的等級標準的前提是存在“分數在相同等級邊界線上的考生，表現出等量可識別的成就特征”[18]；在不同的考試中應用相同的標準[17]；可比性是雙方或多方之間正式接受的兩項或多項等效的資格[19]。通過定義間的比較可以發現，考試的可比性與“標準”的劃定密切相關，考生的能力水平一般通過是否達到某種“標準”來反映。

學科之間的可比性一直存在爭議。反對科目成績具有可比性的學者認為，各科的學習內容與所需能力不同，如同蘋果與橙子一樣難以比較。也有學者持不同看法，認為有一種共通的學業能力貫穿于學科之間，而且要滿足成績使用者的期望，就有必要考慮這個問題。[20]持“可比”觀點的學者認為，根據不同事物之間存在的特定屬性能夠進行比較。如蘋果和橙子的比較，可以根據“甜度”建立等價的關系，一定數量的蘋果對應一定數量的橙子。在教育測量領域，基于考試結果使用的要求，需要對不同科目進行比較。一般根據考生的能力水平所設定的公共等級標準建立相應的等價關系，使科目1的某個等級對應科目2的某個等級。

可比性主要使用“數理統計”和“專家判斷”兩類方法。數理統計法主要基于以下原則：一是通過數據檢測和比較標準；二是確定達到等級的學生數量和比例；三是通過其他相關數據來控制數量和比例。判斷法主要是通過專家經驗對與等級評定相關的材料進行人工評判。比較“標準”主要包括兩個方面：一是感知大綱和相關材料的要求；二是感知考生答題的質量。然而，“統計”方法和“判斷”方法并不是嚴格區分的，通常根據統計結果進行判斷，如根據往年數據判斷當年等級的變動情況。

（二）“等效”（Equivalence）與“等值”（Equating）

“等效”與“等值”都是實現測驗科學與公平的重要途徑。二者最主要的區別在于是否能應用于“非并行版本”的測驗，即測驗“等值”僅能應用于相同科目多次測驗之間的可比性問題。具體而言，二者的區別表現在三個方面。

第一，兩者的概念邊界有所區別。“等效”是指“價值或重要性相等”，是一種主觀的衡量標準。“等效”的功能與貨幣的價值尺度職能相類似。貨幣的價值尺度職能是把各種商品的價值都表現為一定的貨幣量，以表示各種商品的價值在質的方面相同，在量的方面可以比較；“等效”是把不同科目的價值表現為一定的標準，以表示不同科目的價值相等，在等級標準上可以進行比較，即在同一等級標準體系下，不同科目的考試成績相同，則被認定為考生具備的能力水平相同，考生在等級或分數上可以進行比較。以數學科目為例，數學相較于其他科目測量的內容和能力不同，考核的是多種心理品質，因此呈現出不同的測量結果。數學和其他科目不是同質的，不同的方面將引起個體之間的差異反應。[21]

測驗等值的理論基礎是“單維度”（unidimensionality）假設，即每個大綱與之相關的測驗，評估的是相同的基礎能力。[22]等值是標準化測驗中的一個必備程序，將測量同一特質的不同測驗版本的分數置于同一尺度上，使得參加不同測驗版本的考生的分數可以直接相比，從而實現跨測驗版本考生評價的公平性。[23]等值是一個統計過程，用于調整不同形式的測驗分數，以便不同考試之間可以互換使用。“等值”是調整難度和內容相似的考試之間測驗難度的差異。[24]測驗等值是假設一個共同的“維度”測試量表，然后允許來自參加測試A的特定群體的個體在測試B中被賦予“等值”的分數。其基本目的是通過數學轉換，將測試A的分數按比例轉化為測試B的得分。[25]

第二，在應用方面，測驗等值中所說的測驗分數系統的轉換與測驗原始分數轉換為量表分數不同。等值是為了將不同測驗形式的分數轉換到同一個分數量表上，以便不同測驗形式的測驗結果之間可以進行比較。將測驗原始分數轉換為量表分數，是為了將一個實測分數轉換到可評價個體相對地位的分數系統中去。等值至少是兩個測驗形式之間的關系。原始分數轉換是同一測驗的不同分數系統之間的轉換，并不一定存在兩個測驗。從本質上說，測驗等值就是通過對考核同一種心理品質的多個測驗形式作出測量分數系統的轉換，進而使得這些不同測驗形式的測驗分數之間具有可比性。[26]

第三，在影響因素方面，兩個測驗形式之間如果是等值的，即使選用不同的被試群體，所測量的結果也相同，不受其他因素的影響。而等效實現的是每一科目的測量結果達到錄取所要求的共同標準。如果科目之間的測驗是等效的，盡管不同科目測量的考生心理品質不同，在難度、信度、成績分布等方面也有差別，但在相同的等級上所反映出的考生的能力水平是一致的。

（三）考試可比性理論的實踐

根據“連接”（linking）方法的分類，通常使用“量表化”（scaling）的方法實現科目間的可比。[27]應用于選考科目可比性的方法可以分為兩類：一是“基于錨測量的量表化”（Scaling to Anchor）；二是“基于假設總體的量表化”（Scaling on Hypothetical Population）。在中國香港和澳大利亞，選考科目的計分分別使用了相應的方法。

1.基于錨測量的量表化方法的應用

香港中學文憑考試大致相當于“高考”，通常由4門主修科目和2-3門選修科目組成，最多可以報考8科。主修科目包括中文、英文、通識教育和數學；考生根據個人特長和興趣，從物理、化學等21門選修科目中自主選擇2-3門科目的組合參加考試，而不局限于以往的文科、理科、商科的組合。考試成績還有一部分來自學生的“平時成績”，占比15%~30%。

在選修科目的設定水平與維持水平上，香港考評局利用組別能力指數作為選修科目評級的參考。組別能力指數是利用統計方法計算出的一組百分比，以得到一組建議臨界分數。對于應考某門選修科目的全體考生來說，他們在核心科目取得某個等級的人數，被用來計算該選修科目在相應等級的組別能力指數。組別能力指數基本上可視作一組百分比，用作選修科目和應用學習科目評級的參考。計算某科目X某個等級或以上（例如第3級或以上）的組別能力指數P的公式如下：

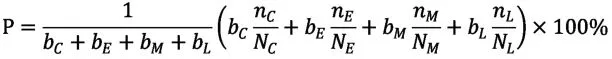
2.基于假設總體的量表化方法的應用

澳大利亞高校根據“高等教育入學排名”（Australian Tertiary Admission Rank，ATAR）進行招生錄取。由于澳大利亞各州的考試制度不同，“高等教育入學排名”的依據略有不同。以新南威爾士州為例，根據考生的“高中畢業證書考試”（High School Certificate Examination,HSC）成績進行計算。通常高中畢業證書考試有八十多個科目，英語為必考科目，其余全部為選修科目，考生可以根據自身的興趣特長和高校的要求自主選擇相關科目參加考試。

在計分過程中使用AMS（Average Marks Scaling）方法將不同科目的HSC分數進行調整，以實現統一測量尺度下的可比。接下來，根據相關文獻[29]對該方法予以簡化說明。

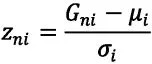
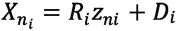
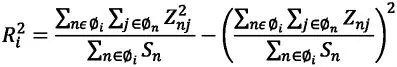
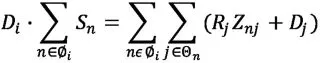
3.量表化方法的局限性

實現多學科不同選考科目之間的可比性，兩種量表化方法都存在一定的局限性。“基于錨測量的量表化”方法與科目設置密切相關。在中國香港，中學文憑考試各必修科目的設置較為均衡，測試內容較能準確反映考生的能力水平，因此可以將必修科目的成績作為依據來校準考生選考科目的成績。其基本假設為：“主修科目”成績優秀的考生，其相關選考科目的成績也是優秀的。

澳大利亞各州的高中畢業證書考試，僅有英語一門必考科目，如果將其作為選考科目的校準依據，則有失偏頗。“基于假設總體的量表化”方法則彌補了上述不足，但校準過程相對復雜，需要具備一定的數理統計知識才能夠理解，校準程序的信息透明度較低。

（四）多學科選考的分數合成：以香港中學文憑考試為例

為了更加科學合理地選拔人才，采用多學科選考科目設置的國家或地區往往采用多元化的錄取方式。中國香港在這方面走在了前列。香港高校一般會針對所有考生提出一般入學要求，作為對考生的最低要求；在一般入學要求的基礎上，特定專業會提出對考生的最低限度要求，在一些科目上會高于一般入學要求，并對選修的科目進行限制。香港中學文憑考試在招生錄取中的應用有四個特點。

其一，按照“科目權重乘以等級”的合成總分的方式進行招生錄取。值得注意的是，香港高校的總分合成錄取，是針對已經達到最低入學要求的考生為選擇相關專業而進行的總分合成，且不包括“體育人才”“校長提名”等方式入學的考生。其二，招生院校劃定一般入學要求。如香港城市大學的一般入學要求為英語3等、中文3等、數學2等、通識教育2等，選修科目1、2均為3等。其三，學院與專業在學校最低入學要求的基礎上，根據專業特點上調相應科目的等級要求。如香港城市大學的BBA會計專業，要求數學成績為3等，比一般入學要求規定的數學成績為2等要高。[30]其四，高校對考生的專業能力存在基本要求。這反映在考生報考專業對選修科目的具體要求上。多數專業都對選修科目有1項要求，少數專業對兩門選修科目有兩項要求。表1列出了2017年香港城市大學會計系工商管理學士的錄取權重。

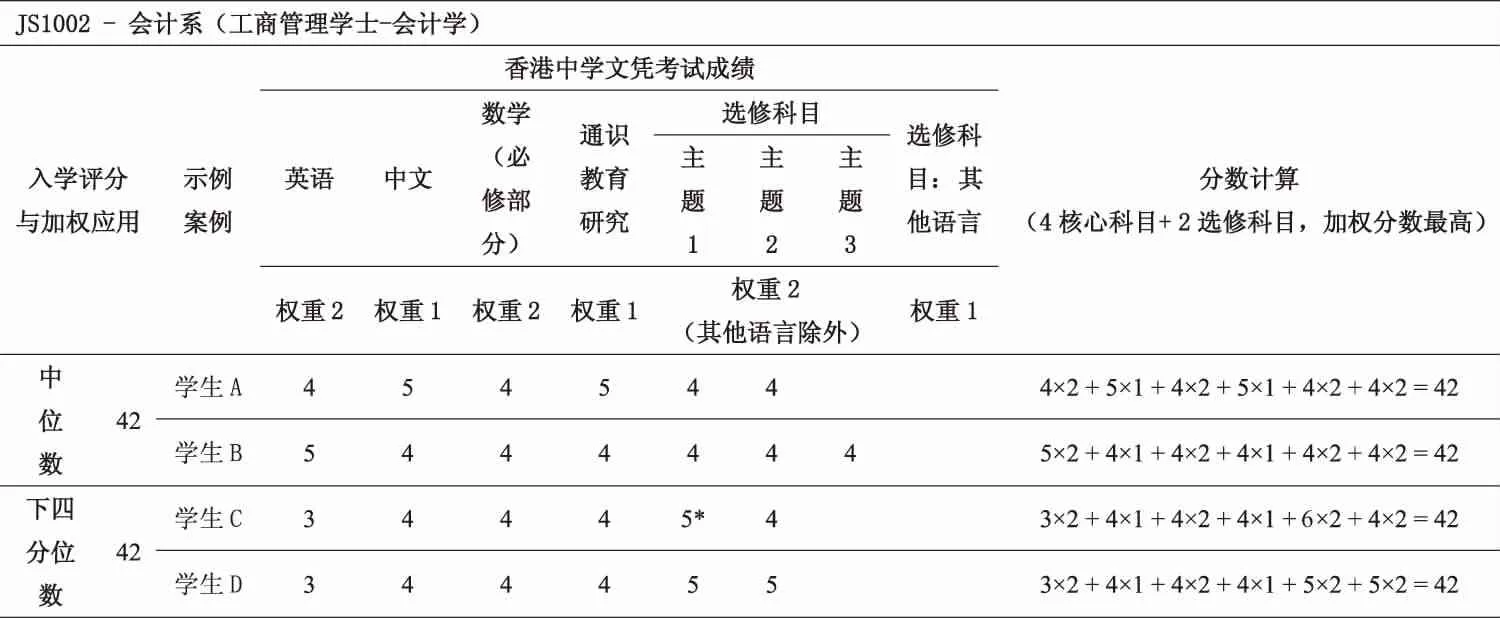
表1 2017年香港城市大學會計系工商管理學士錄取權重

四、政策建議

（一）對新高考選考科目計分開展“量表化”方法研究

應以海南試點計分政策改革為契機，探索適合新高考科目設置的“量表化”計分改進研究。海南作為高考使用標準分的地區，提出了“統一高考科目、學業水平等級性考試各科的成績以及高校錄取總成績均以標準分呈現”[31]的分數報告方案。與其他試點不同，海南使用以標準分為基礎的分數報告方式，并沒有提出劃定等級。為此，應積極推進海南試點計分政策改革，根據統考科目與選考科目設置現狀，積極吸收國內外先進計分經驗，開發出符合新高考實際的量表化方案，以實現海南“根據各學科質量因素對考生成績先行校準、等值處理后再進行標準分轉換，以確保公平公正”[32]的計分設計。

值得注意的是，考試可比性往往通過數理統計與專家判斷相結合的方式實現。使用單一的方法并不能較好地解決可比性問題，專家的判斷不可或缺。有研究認為，當專家做出整體判斷時，可以對考生的不同能力水平進行不同方面的補償。[33]專家對標準的判斷應當得到數理統計證據來源的支持。[34]

（二）調適“總分錄取”政策，科學合成分數

高考主要服務于高等學校人才選拔，因此，需要強化高校在招生考試中的權利。其前提是，需要改進“總分錄取”政策。在新高考中，學生不僅僅要關注報什么學校，更需要關注讀什么專業，把自己高中學習的特長與將來的志愿結合起來，并進一步發展為自己的職業專長。[35]這些變革要求高校重視學科在招生中的地位。在試點階段，除少數高校外，考慮到生源問題，多數高校沒有或較少對選考科目進行限制，這將不利于學生的職業生涯發展和高校的專業教學。

為此，應進行相應的政策調適，以緩解考生報考的功利性心理，避免高校之間在錄取總分上的競爭，為科學合成分數創造政策空間。其一，所有高校的全部招生專業均應根據專業特點，設定選考科目要求。其二，將選考科目成績及其他相關考試測驗信息作為高校錄取的依據之一，高校設置相應的錄取規則。其三，積極開展新高考分數合成方式研究，優化成績報告方式，為高校招生錄取提供科學依據。