將橢圓曲線分解算法擴展為三階段的方案

羅貴文

?

將橢圓曲線分解算法擴展為三階段的方案

羅貴文1,2

（1. 中國科學院大學網絡空間安全學院，北京 100049；2. 中國科學院信息工程研究所信息安全國家重點實驗室，北京 100093)

橢圓曲線法是目前使用最廣泛的整數分解算法之一，最早由Lenstra于1985年提出，原始的算法只有第一階段。自其提出以來，圍繞算法和實現的研究層出不窮，最重要的改進是Brent和Montgomery提出橢圓曲線法的第二階段，這極大地提升了橢圓曲線算法的分解能力和效率。將橢圓曲線法擴展為三階段，采用的方法是將第一階段和第二階段進行“融合”。對比目前流行的兩階段橢圓曲線法，改進后的算法有兩方面的優點：一是在保持同兩階段橢圓曲線法參數相同的情況下，通過增加微不足道的消耗，提升找到因子的概率；二是在搜尋同一個因子時，可以使用較小的“光滑參數”。

整數分解；快速分解；橢圓曲線法；光滑參數

1 引言

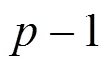
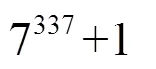
2005年，Zimmermann等在文獻[5]中總結了20年來橢圓曲線法的發展，并在文末提出一個開放問題：是否有可能設計“第三階段”，進一步提升橢圓曲線法的分解能力？可惜的是，目前并沒有發現這一方向的進展。本文通過將第一階段和第二階段進行“融合”，把橢圓曲線法擴展為三階段，以期提升橢圓曲線法搜尋大素因子的能力。文中提出的新算法可以從兩方面加以利用：一是在保持同兩階段橢圓曲線法參數相同的情況下，通過增加少許計算量，提升算法找到因子的概率；二是在搜尋同一個因子時，可以減小“光滑參數”的值。

2 橢圓曲線分解算法

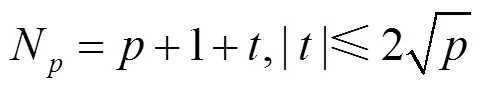
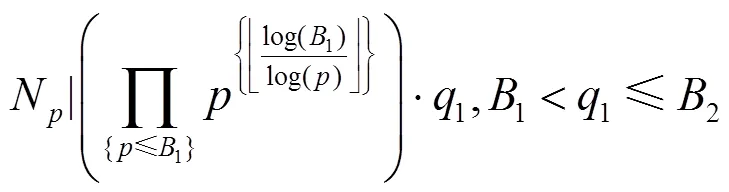
算法1 兩階段的橢圓曲線分解算法

輸入 既不能被2整除又不能被3整除的整數，以及光滑參數1≤2

輸出的因子或FAIL

1) 任選橢圓曲線mod及該曲線上一點0=(0:0:0)

2) 在曲線mod上計算

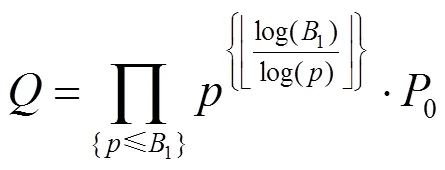
3) 設=(x:y:z)，計算=gcd(,x)

4) 如果≠1，輸出并終止，否則繼續

5) 對每個素數(1<≤2)

6) 計算(x:y:z)=?

7) 計算=gcd(,x)

8) 如果≠1，輸出并終止

9) 輸出FAIL

3 橢圓曲線法擴展為三階段

本節提出一種算法1的改進算法，將橢圓曲線法擴展為三階段。通過增加較小的計算量，提高橢圓曲線分解算法做出分解的可能性。如算法2所示，使用3個“光滑參數”1、2、3(1<2≤3)。算法2的步驟1)~步驟4)稱為第一階段，步驟5)～步驟7)稱為第二階段，步驟8)~步驟11)稱為第三階段。

與算法 1對比，算法2的第一階段與第三階段分別相當于算法1的第一階段和第二階段。若

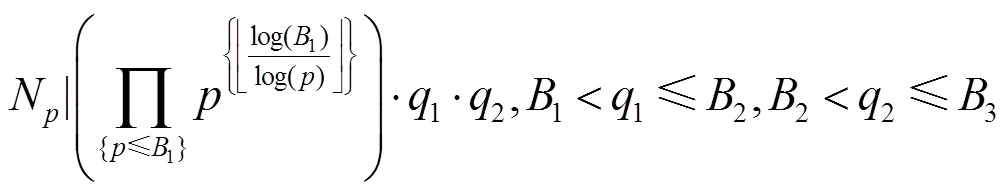
那么算法2有一定概率找出的素因子，這里所有的和1、2均為素數。

算法2 擴展到三階段的橢圓曲線分解算法

輸入 既不能被2整除又不能被3整除的整數，以及光滑參數1、2、3

輸出的因子，或FAIL

1) 任選橢圓曲線mod及該曲線上一點0=(0:0:0)

2) 在曲線mod上計算

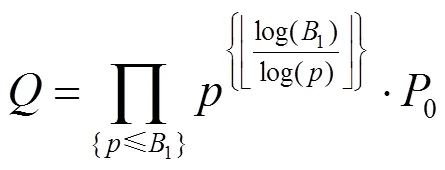
3) 設=(x:y:z)，計算=gcd(,x)

4) 如果≠1，輸出并終止，否則繼續

7) 如果≠1，輸出并終止，否則繼續

8) 對每個素數(1<≤3)

9) 計算(x:y:z)=?1

10) 計算=gcd(,x)

11) 如果≠1，輸出并終止

12) 輸出FAIL

預先取定整數1、2，將算法1中的“光滑參數”取為1、2，將算法2中的“光滑參數”取為1、2、3，算法2的第一階段與第三階段分別等同于算法1的第一階段和第二階段。如果N最大的素因子不超過2，并且第二大的素因子不超過1，那么算法1可以找出的素因子；如果N最大的素因子不超過2，第二大的素因子不超過2，并且第三大的素因子不超過1，此時算法1便束手無策，但算法2卻有可能找出的素因子。因此算法2新設計的第二階段增大了橢圓曲線法成功分解的概率，增加的消耗是個橢圓曲線標量乘運算。

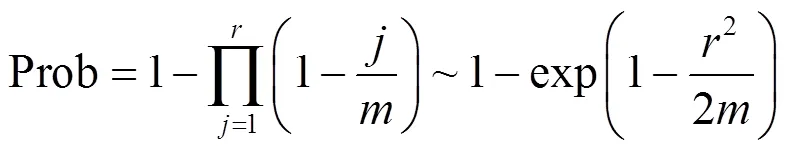
4 實踐

第3節闡述了算法2在增加少許計算量的情況下，相比算法1提高了成功分解的概率。從另外一個角度考慮，在搜尋同一個素因子時，算法2可以適當減小“光滑參數”。下面以具體實踐來闡述這一論斷。

2018年“第三屆全國高校密碼數學挑戰賽”賽題二要求參賽選手分解一個432十進制位的大整數，在將所有小素因子找出后，最困難的部分是分解一個116十進制位的整數=18311422666613585891834635740997396678045469120835214703400815986739539158582260051188900502060268468088445260535641。

使用算法2對進行分解，分別取3個“光滑參數”，1=3×106，2=3=1×109，取

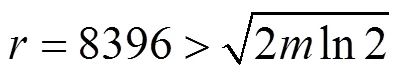
該橢圓曲線的階為N。

N=25?3?5?7?353?1439?4231?20929?28753?1445533?1533487?2283881?306842093?512194063

若按照 GMP-ECM 7.0.4推薦的搜尋60十進制位素因子的參數設定，1=2.6×108，2=3.2×1012，并利用算法1，使用該橢圓曲線無法成功分解出這一58十進制位素因子。

5 結束語

本文將目前流行的兩階段橢圓曲線法擴展為三階段，并通過理論分析和實踐，從兩方面闡述了改進后算法的優點，一是在保持同兩階段橢圓曲線法參數相同的情況下，通過增加微不足道的消耗，提升找到因子的概率；二是在搜尋同一個因子時，可以使用較小的“光滑參數”。此外，改進后的算法可能有能力搜尋更大的素因子。橢圓曲線法的瓶頸主要在第一階段消耗過大，利用算法2，可以適當減小1，增大2與3，從而增強使用橢圓曲線法搜尋更大素因子的能力。

致謝

感謝吳寶峰、呂麗君在成文過程中和我進行諸多有益討論，并提出寶貴意見。

[1] LENSTRA H. Factoring integer with elliptic curves[J]. Ann of Math, 1987, 126.

[2] BRENT R P. Some integer factorization algorithms using elliptic curves[J]. Australian National University Technical Report, 1985, 8:149-163.

[3] MONTGOMERY P L. Speeding the pollard and elliptic curve methods of factorization[J]. Mathematics of Computation, 1987, 48(177): 243-264.

[4] MONTGOMERY P L. An FFT extension of the elliptic curve method of factorization[M]. University of California at Los Angeles, 1992.

[5] ZIMMERMANN P, DODSON B. 20 years of ECM[C]// International Algorithmic Number Theory Symposium. 2006: 525-542.

[6] The gmp-ecm development team, GMP-ECM, an implementation of the elliptic curve method algorithm, release 7.0.4[R]. 2017.

[7] OKEYA K, KURUMATANI H, SAKURAI K. Elliptic curves with the montgomery-form and their cryptographic applications[C]//International Workshop on Practice & Theory in Public Key Cryptography: Public Key Cryptography. 2000.

[8] MONTGOMERY P L. Evaluating recurrences of formx+n=(x,x,x?n) via Lucas chains[M]. 1983.

[9] TALL A. A generalization of the Lucas addition chains[J]. Bulletin mathématique de la Société des Sciences Mathématiques de Roumanie, 2012: 79-93.

[10] MONTGOMERY P L. An FFT extension of the elliptic curve method of factorization[D]. Los Angeles: University of California, 1992.

[11] JOACHIM V Z G, GERHARD J. Modern computer algebra[M]. Modern Computer Algebra. 2001.

[12] HANROT G, QUERCIA M, ZIMMERMANN P. The middle product algorithm I[J]. Applicable Algebra in Engineering, Communication and Computing, 2004, 14(6):415-438.

[13] BERNSTEIN D, BIRKNER P, LANGE T, et al. ECM using edwards curves[J]. Mathematics of Computation, 2012, 82(282):16.

[14] BERNSTEIN D J, BIRKNER P, JOYE M, et al. Twisted edwards curves[J]. Lecture Notes in Computer Science, 2008, 5023: 389-405.

[15] BERNSTEIN D J, HENINGER N, LOU P, et al. Post-quantum RSA[C]//International Workshop on Post-Quantum Cryptography. 2017: 311-329.

Scheme of extending elliptic curve method to three phases

LUO Guiwen1,2

1. School of Cyber Security, University of Chinese Academy of Sciences, Beijing 100049, China 2. State Key Laboratory of Information Security, Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China

Elliptic curve method for integer factorization (ECM) is one of the most popular integer factorization algorithms, and it was firstly proposed by Lenstra in 1985. The original ECM contained just first phase. Since its invention, researches about the algorithm and implementation emerged up, among which the most important improvement is the extension to two phases proposed by Brent and Montgomery. This improvement tremendously strengthened ECM's capacity and efficiency. Elliptic curve method was extended to three phases. Extension method is kind of like “mixing together” the first phase and second phase. Compared to the best current two phases ECM, the new algorithm shows 2 advantages. First, under the same factorization parameters, the proposed algorithm improves the probability of finding out prime factor at the expense of negligible increasement of time. Second, when searching the same prime factor, the proposed algorithm can utilize smaller “smoothness parameters”.

integer factorization, fast factorization, elliptic curve method, smoothness parameter

TP301

A

10.11959/j.issn.2096-109x.2018101

2018-11-02；

2018-11-28

羅貴文，louguiwen@iie.ac.cn

國防科技創新特區基金資助項目（No.Y7H0041102）

The National Defense Science and Technology Innovation Foundation (No.Y7H0041102)

羅貴文（1993-），男，重慶人，中國科學院大學碩士生，主要研究方向為橢圓曲線密碼學。