“實數大小比較”有妙招

蔣根林

（作者單位：江蘇省南京市科利華中學）

數系擴充到實數后，數的概念范圍擴大了，我們已步入實數的殿堂.在有理數范圍內可以進行數的大小比較，那么學習無理數以后，在實數范圍內如何進行數的大小比較呢？下面結合具體例題給同學們總結歸納.

妙招1：數形結合法

【例1】比較大小：-，-2．

【解析】我們知道邊長為1的正方形對角線長為 2，于是先在數軸上畫出表示-的點，如圖：

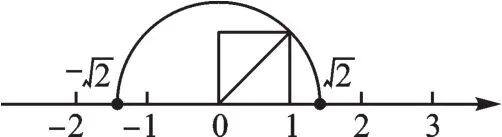
【回顧】事實上，我們還可結合勾股定理，利用數軸來比較-、-等的大小.

妙招2：“回到概念”法

由于數學概念本身有“雙向性”：“正向”與“反向”，所以，在用概念時就有“正用”和“反用”兩種方法.

【例2】比較-與-的大小．

【解析】比較兩個負數的大小，可先比較它們的絕對值，絕對值大的反而小.由于，3的算術平方根為，2的算術平方根為，因為3＞2，所以＞，故-＜-.

【回顧】我們借助平方根、立方根的意義，對它們的概念作出分析，從中悟出道理：一個較大的非負數的算術平方根較大；一個較大數的立方根較大.然后加以應用，問題獲得解決.

【例3】比較大小：

【解析】（1）因為是140的算術平方根，可反用平方根概念，所以（）2=140.

又因為122=144＞140，所以＜12.

又因為（2.5）3=15.625＞9，所以＜2.5.

【回顧】這里主要是對平方根、立方根的概念逆向思考.一個非負數a的平方根為：±，反過來，（±）2=a（a≥0）；一個數a的立方根為，反過來，（）3=a.上面的求解就是反用概念的“平方法”或“立方法”.

妙招3：估值法

【例4】比較大小：+2______

【解析】由于4＜＜5，所以6＜+2＜7，又由于＞7，所以+2＜

【回顧】對于能直接估計出大小的兩個平方根的大小比較時，我們應該首先考慮用估值法比較兩個平方根的大小，因為這種大小比較的方法最直接.對于有些無理數，我們可以綜合平方根或立方根的知識，來一個兩頭“夾逼”，找出與這些無理數緊相鄰的兩個完全平方數，確定這個無理數所在的范圍，然后再與其他數比較大小.

妙招4：特值法

【例5】若0＜a＜1，直接比較、的大小.

【解析】因為0＜a＜1，若a=

【回顧】特值法對于處理“直接填寫答案”的題型（包括填空、選擇題型）很有效果.對于解答題或數學研究來說，特值法是“以退為進”策略的具體化體現，通過賦值分析，往往能發現規律、提示解答方向，是一種很有意義的求解策略.