基于回歸解法的預應力錨桿對邊坡穩定系數的影響研究
馮是明
(江西省水利水電建設有限公司,江西 南昌 330025)
預應力錨桿是一種主要利用拉應力來對邊坡或地基土體產生支撐作用的新型巖土工程技術,主要由錨頭、自由端以及錨固段3個結構所構成:其中錨頭為錨桿外端,主要作用為鎖定錨桿拉力;自由端則為錨頭和錨固段2者之間的部分,主要作用為拉力的傳遞以及耦合錨頭部分來產生錨固段上的預應力;錨固段是直接與土體或巖體接觸的部分,其作用主要是進行拉力的傳遞,將拉應力傳遞到土體或巖體結構上。從預應力錨桿的工作原理可以看出,預應力錨桿產生的預應力主要為拉應力,且應力的傳遞作用所依賴的結構強度主要取決于桿體、錨固段自身材料強度及錨固段和土層接觸部分的黏結強度。
預應力錨桿作為當前的一種新型地基和邊坡加固方式,在大量水利工程及巖土工程中已經被廣泛利用,這種加固方式的產生有著比較漫長的發展史,其產生的原理為傳統的錨桿支護方式,因此也有著一定的理論和實踐基礎。陳尤等[1]通過利用錨桿對巖質邊坡進行加固研究,探討了布置參數對加固效果的影響,并進行了優化設計;祁磊等[2]采用數值分析方法,從插值的角度對錨桿安裝方法與邊坡安全系數之間的相關性進行了分析;郭清順[3]通過對深基開挖過程中的錨桿支護施工技術進行探討,對預應力錨桿支護的應用進行了研究;王輝[4]基于能量原理,對預應力錨桿在復合土釘支護體系中的應力進行了分析研究;侯小強等[5]以高邊坡為研究對象,研究了框架預應力錨桿在高邊坡中的加固機理,并進行了優化設計研究;此外,還有眾多學者[6- 10]也對錨桿加固進行過深入研究。本文基于前人的研究成果,利用Phase2D數值模擬方法,通過繪制預應力錨桿數值計算單元體系,建立了某邊坡的錨桿加護后的計算模型,并從錨桿布置角度、間距以及布置位置3個方面分析了錨桿布置參數與邊坡安全系數之間的相關性,此外,通過多元線性回歸計算方法,對錨桿布置參數與邊坡安全系數之間的關系進行了歸一化處理,得到了定量的關系表達式。
1 預應力錨桿加固邊坡原理
邊坡穩定性安全系數是以沿滑裂面抗滑力與滑動力的比值進行定義的,當該值大于1.0時,認為坡體是穩定的;而當小于1.0時,認為邊坡具有發生破壞的可能。當前比較常見的邊坡穩定性分析方式一般為剛體極限平衡分析法,這種方法的定義方式為:
[Fs]=抗滑力(矩)/致滑力(矩)
(1)
通過充分利用巖體和錨桿兩者之間的共同作用力,使用預應力錨桿來對邊坡進行加固,能夠及大幅度的改善邊坡巖體的穩定環境。其主要作用有兩點:①在預應力的作用下,不穩定滑體受到較高圍壓的作用,使得滑體處于三向應力狀態下,因此巖體的強度與變形能力相對于單向應力下來說要高許多,使得邊坡更穩定;②在錨桿的錨固力的直接作用下,滑面上的應力狀態以及邊坡穩定性條件都發生了很大程度的改變,從圖1—2的應力分析能夠推導出,因預應力錨桿作用所產生的錨固力施加的抗滑阻力(Qtf)應為:
Qf=Qntanφ+Qv=Qt[sin(α+θ)tanφ+cos(α+θ)]
(2)
式中,Qt—錨桿拉力;Qv、Qn—Qt在滑面及法向上的切力;φ、α、θ—滑面內摩擦角、傾角及錨桿傾角。
從式(2)能夠看出,預應力錨桿在滑面上主要從增大抗滑阻力(Qv)和正應力(Qn)2個方面來增大抗滑面的摩擦阻力。由此可見,對邊坡需用安全系數值,即允許最小安全值的合理選取,是邊坡錨固工程中應該首先考慮的問題。
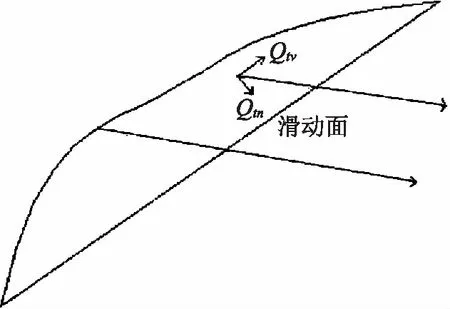
圖1 預應力錨桿的抗滑作用
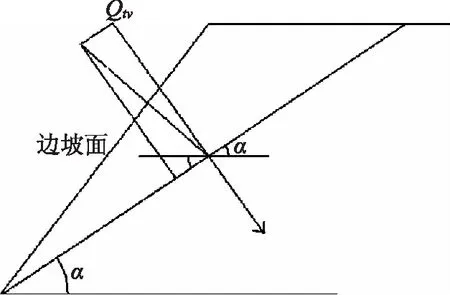
圖2 滑面上的錨固力
2 工程實例
工程邊坡地處云貴高原與長江中下游過渡帶,其地勢條件主要為北、西、南三面較高,而中間地帶較低并向東方向傾斜,該區域地形地貌以山地為主,地層上主要由白堊系泥質粉砂巖、含有軟弱薄夾層的泥巖和頁巖等組成,這些巖石多為軟巖,且因受多次地質作用,其節理裂隙比較發育,破碎帶較多,巖體結構完整性較差,本次研究的邊坡數值模型如圖3所示。
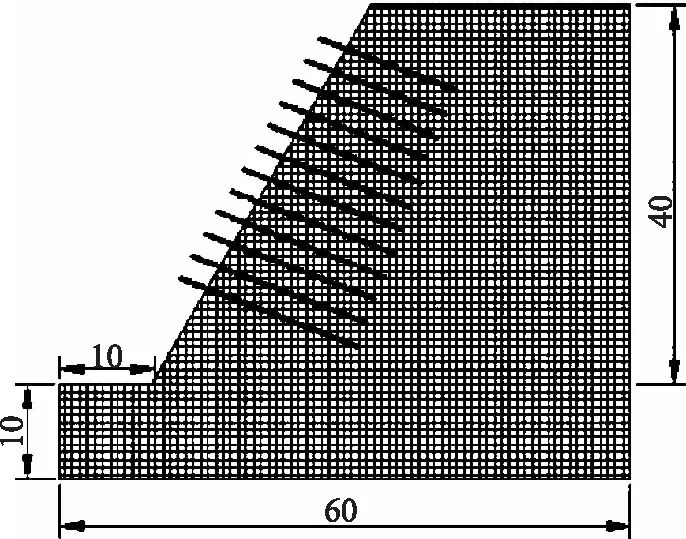
圖3 邊坡數值模型
該邊坡水平方向長約為60m,豎直高度約為40m,且坡面與水平方向的傾角約為60°,為了對邊坡在加固前和加固后的穩定性進行分析,以測得的表1所示邊坡巖性物理參數來作為依據,并利用Phase2D數值模擬軟件來建立三維數值模型。模型單元上,為包含1500個單元以及3000節點的邊坡模型;邊界條件上采用的是上部為自由邊界、下部固定約束和左右兩側為水平約束;理論方面所并采的是剪切拉伸破壞理論下的摩爾-庫倫強度準則;應力組成上,初始應力場主要考慮的是自重應力;在計算收斂準上,采用的是不平衡力比率求解要求,最終得到的數值計算結果如圖4所示。

表1 邊坡巖性物理力學參數
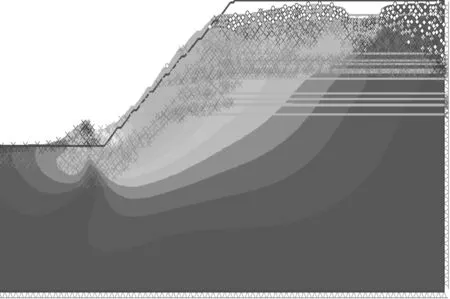
圖4 數值計算結果示意圖
從圖4中可以看到,邊坡的塑形貫通區域內為危險區域,有著十分清晰的潛在滑動面,此外還能根據速度矢量圖看到,在滑動面外側區域部分的各個網格點的滑移速度相比其他區域來說明顯更大,因此能夠判斷出這一結論是正確的,這也證明了該區域的確已經開始出現滑動,可以認為發生了破壞,并根據計算結果得到邊坡安全系數為1.05。
為了研究錨桿在邊坡中的布置方式對于加固作用的影響,選取了多組方案來進行綜合分析,因此先得到了錨桿的物理參數,本文采用的是橫截面積為706mm2的鋼制預應力錨桿,為了進行后續的分析,得到其相關物理參數見表2。
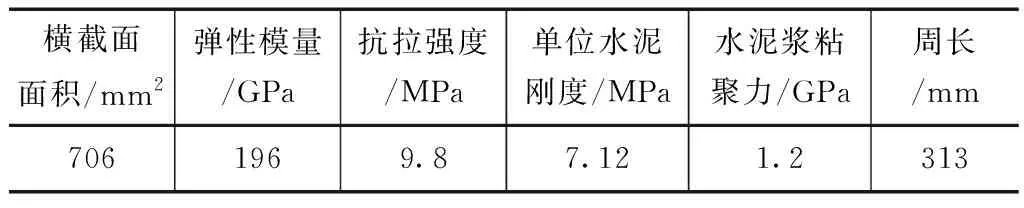
表2 錨桿物理參數
以7m錨桿為例,具體的錨桿布置方案如下:錨桿傾角布置為10°到35°之間進行傾角的依次增加;砂漿厚度的布置為0.1~2.6m之間等間距布置;錨桿間距為0.5~3m來進行位置的布置。利用上述方法進行布置后,通過Phase2D進行邊坡安全系數計算,并根據所得結果進行處理分析,并利用matlab軟件擬合進行關系曲線的擬合,得到圖5—7所示的3個錨桿布置參數與邊坡安全系數的關系曲線。
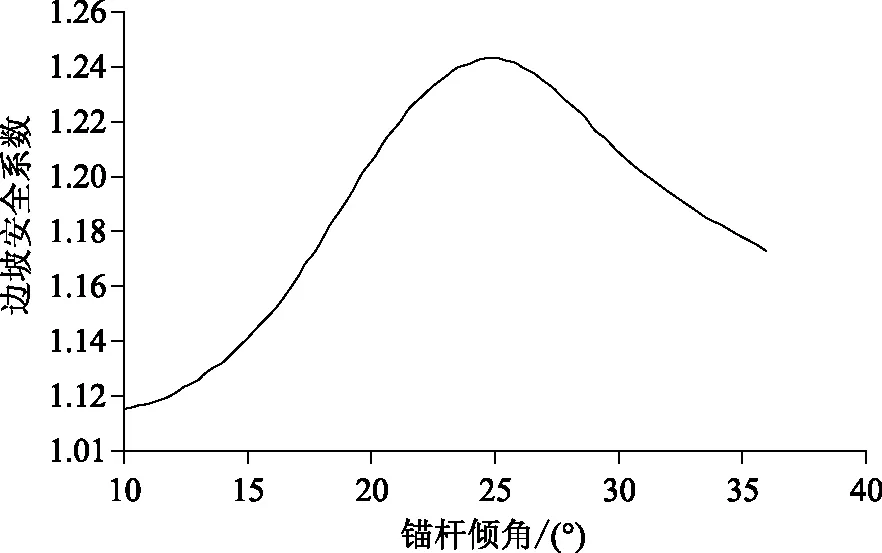
圖5 錨桿傾角與邊坡安全系數的關系

圖6 砂漿厚度與邊坡安全系數的關系
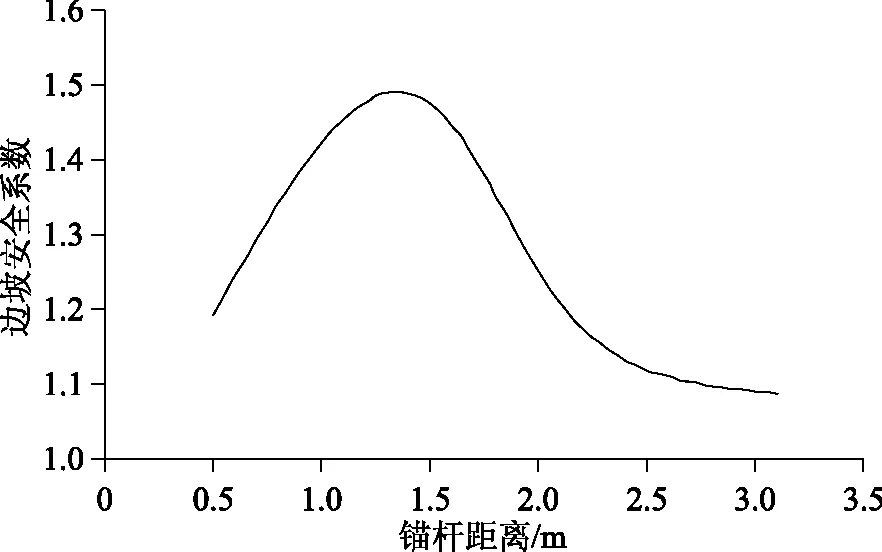
圖7 錨桿間距與邊坡安全系數的關系
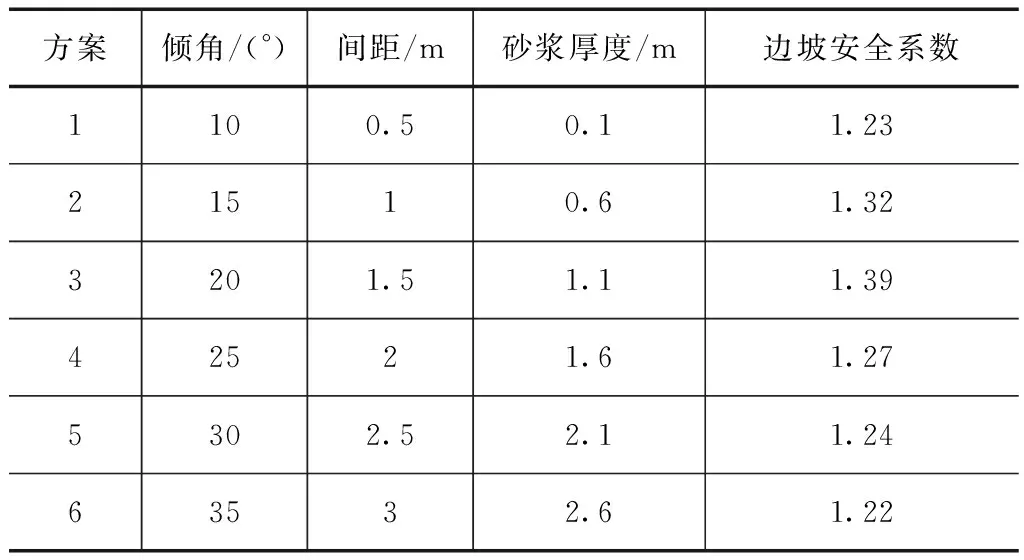
表3 錨桿布置參數與邊坡安全系數
通過圖5—7擬合曲線能夠看出,在進行加固之后,不同錨桿傾角、砂漿厚度及錨桿間距對于的邊坡安全系數的影響不盡相同。隨著錨桿傾角的增加,安全系數先增大后減小,且在傾角在21°~24°區間段的效果為最佳;隨著砂漿厚度的增加,安全系數逐漸增大,且在前期增大較快,而在厚度達到1.5m之后來時緩慢增長,因此1.5m時為最佳錨固厚度;隨著布置間距的增加,安全系數是呈現出二次拋物線變化規律的,從圖7可以看出間距在達到1.4m后安全系數降低比較快,因此在峰值段,即間距為1~1.4m為最佳錨固間距。
3 多元線性回歸求解
多元線性回歸法是一種非常常見的數值處理方法,由于其方法簡單使用,常常被用作工程數值處理方法。設具有一個因變量以及k個相互不關聯的影響因素X1,他們之間存在著如下關系:
Y=β0+β1x1+…+βkxk+ε
(3)
ε~N(0,σ2)
(4)
將式(3)和式(4)稱為多元回歸函數,而βi(i=0,1,2,…,k)則被稱為回歸系數,βi(i=0,1…k)與σ2均未知。設(xi1,xi2,…xik,yi)為(X1,X2…,XK,Y)的試驗數據,且有從揚程的響應曲面圖中可以發現,總體上隨著粗糙度的增加,揚程逐漸減小,葉輪壁面的粗糙度對性能影響大于導葉。在壁面粗糙度初始增加的地方,效率及揚程下降較快,且揚程下降明顯快于效率下降幅度。而當壁面粗糙度大于0.3mm以后揚程幾乎不再發生變化,而效率仍在下降。主要是軸功率仍在上升,引起效率下降。揚程在壁面粗糙度大于0.3mm軸流泵的揚程值幾乎不再下降,并不代表水力損失減小,而是此時因軸功率的增加,葉輪傳遞給流體的能量更多,損失的能量同比增加,最終在揚程上表示為不變。在壁面粗糙度小于0.3mm時,因葉輪傳遞給流體增加的能量不足以彌補因粗糙壁面損失的能量,故整體揚程表現為降低。
(5)
記β=(β0,β1…βk)T,Y(y1,y2,…yn)T,ε=(ε1,ε2,…εn)T
則式(3)表示為:
Y=Xβ+ε
(6)
ε~Nn(0,σ2In)
(7)
由于rk(XTX)=rk(X)=k+1,可以判斷出XTX是存在的,因此能夠得到β為:
β=(XTX)-1XTY
(8)
根據式(6),將x1作為錨桿傾角,x2作為砂漿厚度,x3作為錨桿布置間距,使用y來表示邊坡安全系數,利用表3數據,并將各個錨桿布置參數下的數據帶入公式進行計算,能夠得到回歸系數估值為:
βT=(β0,β1,β2,β3)=(2.2381,-0.0584,0.0121,0.32)
因此得到該樣本下的多元線性回歸方程為
y=2.2381-0.0584x1+0.0121x2+0.32x3
(9)
根據得到的線性擬合方程,得到邊坡安全系數和錨桿傾角、錨桿間距及砂漿厚度各個參數之間的定量關系表達式為:
Fs=2.2381-0.0584α+0.0121l+0.32d
(10)
4 結論
以云貴高原與長江中下游過渡帶某邊坡加固工程為對象,利用Phase2D數值模擬軟件對得到不同錨固參數下的邊坡穩定性進行模擬分析,得到了邊坡安全系數隨錨固參數的變化規律,得到了最佳錨桿傾角、砂漿厚度及錨桿間距,并利用多元線性回歸數值處理法獲得了錨桿布置參數和邊坡安全系數之間的線性表達式。
本文結果對于判斷錨桿支護邊坡來說具有重要依據,該方法得到的數值誤差約為3.41%,在誤差范圍內是合理的,需要指出,由于本方法是基于有限數據進行線性擬合,故有待更多工程現場數據來進行驗證和完善。

