基于SUFI- 2算法和SWAT模型的遼河流域水文模擬及參數不確定性分析

李 昕

(遼陽水文局，遼寧 遼陽 111000)

隨著社會經濟的快速發展，人口數量急劇增加，水源供水壓力巨大、城市用水緊張以及生活污水排放等問題進一步惡化，遼河流域水資源已無法保證人們正常的生活需要，嚴重制約了東北部地區的經濟發展[1]。遼河流域不僅是我國重要的糧食生產基地也是我國東北地區工業發展核心區域。遼河流域作為我國東北地區的主要河流是保障我國工農業用水以及城市生活用水的主要來源[2]。近年來，水資源隨著經濟的發展、環境氣候的惡化以及人類活動日趨頻繁等作用影響而日益減少，水資源供需矛盾和水資源緊缺問題日益嚴峻。為提升水資源管理的科學性與有效性有必要對徑流過程進行精確的模擬分析[3]。流域水文循環和徑流模擬的有效工具之一為給予物理學理論的分布式水文模型。SWAT模型具有參數設置少、操作簡便等優點被國內外學者廣泛應用于農業管理措施對輸送遷移影響規律及不同土地利用模式模擬分析中。

模型參數的相關性以及非線性特征是引起預測結果多樣性或出現局部最優主要因素，其中模型輸入、系統輸出以及系統結構的不確定性為模型主要的不確定性方面[4]。考慮到模型不確定性的復雜性和關聯性，并且模型模擬結果的精度和準確性與不確定性分析結果未存在顯著相關性，因此存在模型與流域的適用性采用目標函數進行檢驗分析的相關研究，而對模型不確定性分析的相關研究相對較少[5- 7]。據此，本文以遼河流域為例并建立SWAT模型，對2012—2015年的月徑流量進行連續預測研究，并對模型的適用性與可靠性進行分析和探討，為提高模型預測結果的準確性提供一定的決策依據和理論支持。

1 流域概況及數據來源

遼河流域面積約21.9萬km2，主要支流有老哈河、大遼河、渾河、太子河等，本文選取大遼河即三岔河與遼陽入海口區段的河流為例進行研究，其集水面積約560km2；年內溫差較大多年平均氣溫8.6℃，多年平均、最大和最小降水量分別為620、980、325mm，其中每年5—9月為汛期降雨量較大[8]。

DEM數字高程數據來源于國際科學數據共享平臺并下載，分辨率為90m×90m并用于研究流域的空間離散化處理；土壤數據包括土壤類型分布和土壤化學屬性值，根據全球土壤質地分類圖同時考慮遼河流域的地質邊界條件設定土壤類型分布圖。環境與生態科學研究中心根據研究流域的邊界特征提供土地利用數據；氣象數據主要包括降雨量、日照時長、風速、溫度、濕度、蒸散發量、太陽輻射等，數據來源于三岔河氣象站和遼陽氣象站實測數據。降雨量數據來源于研究流域內10個降雨監測站在2012—2015年的日降雨量實測數據，較遠距離的區域利用插值法計算日降雨量。依據研究流域市級狀況并結合相關文獻，本文分別選取2012、2013—2014和2015年作為模型預熱期、率定期、驗證期。

2 基本方法

模型不確定分析、敏感性分析、率定為本文主要研究內容，其中SWAT模型敏感性分析發生在模型率定之前。對單個參數進行率定前分析以及若干次迭代計算的敏感性為SUFI- 2算法敏感性分析的2種主要類型，其中若干次迭代運算是將本次迭代作為下次迭代運算的參考和前提[9]。

2.1 SWAT模擬及敏感性分析

本文根據遼河流域的實際情況和DEM數據將其離散為若干個不同的子流域，對土壤、坡度以及土地利用等數據在各子流域上進行疊加分析，然后結合子流域特征進行不同水文響應單元的劃分進而利用氣象數據資料對遼陽水文站的徑流量進行模擬求解[10]。LH-OAT敏感性分析法具有OAT敏感性分析以及LH采樣法的優點和特征，本文采用該方法對SWAT模型進行分析，其中分層式采樣法為LH采樣的主要方法，其特點是以最低的采樣量盡可能覆蓋最優的采樣立方，因此相對于隨機采樣法該方法具有較高的輸出統計效率和特點。通過對模型進行n+1次的運算，確定n個參數中某一參數的敏感性，其特征為在運行過程中其他參數保持不變而按照預定規則改變某一參數。所以，該方法可更加清晰、客觀地反映輸出結果的變化，進而可以更加準確、客觀地揭示輸入參數值的變化狀況及作用規律。為了對參數的敏感性大小進行排序，本文結合研究區域實際狀況和相關標準確定了敏感度取值范圍表，見表1。

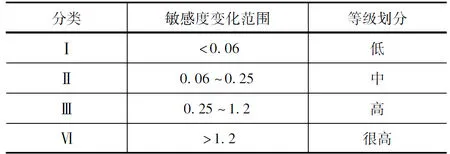
表1 敏感度取值范圍表

2.2 SUFI- 2敏感性分析

SUFI- 2算法的敏感性分析共有以下3種求解方法。

(1)OAT求解法。對參數的敏感性僅需進行一次計算并假定其他相關參數保持不變。該方法具有2個基本優點，即不僅可對SWAT敏感性結果進行檢驗和判斷，而且所求得的參數敏感程度可發生在整體率定之前。

(2)全局敏感度求解法。在率定過程中可對下次需要率定的參數敏感性求解和計算。相對于臨界值T統計量的假設檢驗樣本值越大則檢驗結果越優；對各個樣本的相對顯著性可利用T檢驗值進行判別，其中P概率值對應于T檢驗值查表，而T統計量可由P概率值進行表征和體現。該方法敏感性參考依據為T絕對值，其絕對值越大則敏感性越高；并且對T值的顯著性可利用P指標進行表征，P值越低則其顯著性越高。

(3)觀察散點圖求解法。對模型模擬的目標函數值利用散點圖進行排序和羅列，首先設定目標函數相關范圍要求并盡可能保證參數敏感性區間縮小至該范圍區間之內。

2.3 率定方法及分析

分別選取標準誤差RMSE、效率系數NSE、修正系數bR2以及確定性系數對模擬值與預測值進行分析并對SWAT模型模擬效果進行綜合評價，其中確定性系數R2公式如下：

(1)

R2值結果為1時則代表模擬值與期望值具有相同的變化趨勢，其值偏離1的程度則代表二者的吻合程度。

采用修正公式bR2對確定性系數進行修正并以此避免其具有的缺點和弊端，其中回歸系數與確定性系數R2的乘積為Φ，計算公式如下：

(2)

Φ值可反映模擬值與觀測值之間的變化規律和變異程度。

效率系數NSE可按下述公式進行計算：

(3)

效率系數NSE值趨近于1的程度代表了模擬值與觀測值之間的偏離程度，即越趨近于1則偏離程度越低。

按下述公式對標準誤差進行求解：

(4)

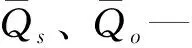
2.4 SUFI- 2不確定性分析

SUFI- 2為考慮了觀測數據、模型結構、參數以及輸入數據的參數估計最優法，可對率定后參數的變化區間進行反映。其中大多數觀測數據分布于95%置信水平上的不確定性區間，并且可在97.5%和2.5%的累積分布上對模擬結果的總的不確定性進行求解，從而可利用拉丁超立方法進行求解并完成輸出，然后對參數的不確定性可利用兩個指標進行確定，R值越趨近于0則預測數據貼近于實測數據的程度越高。

3 結果及討論

3.1 參數敏感性分析

在率定之前可利用SWAT自帶敏感性分析模塊進行分析，在率定之后可利用SUFI- 2法進行全局敏感性分析[11]。因此，在率定之前可依據SWAT敏感性分析結果對全部參數進行分析。并且在率定之間對單參數可利用SUFI- 2的OAT法進行敏感性確定。據此，該分析方法具有更好的效果和客觀性，個別參數統計分析見表2。

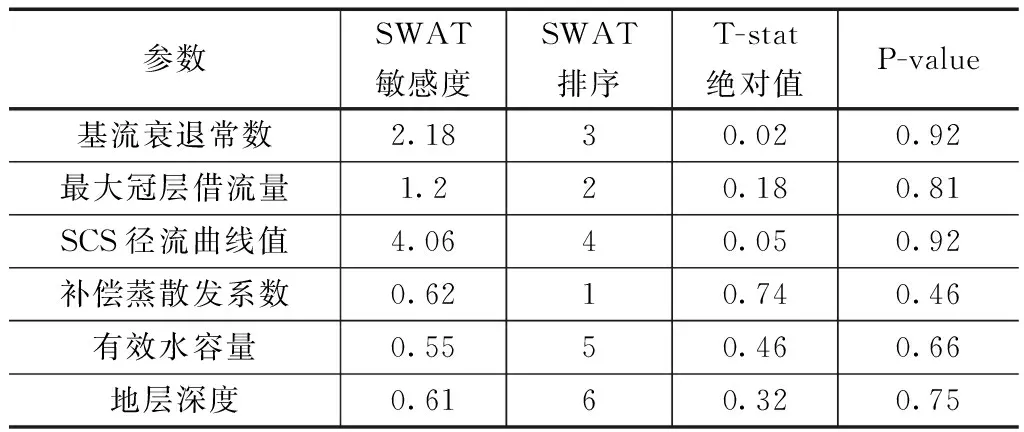
表2 部分參數敏感性分析結果

3.2 參數率定及模型驗證

為降低初始條件對預測結果的不利影響，按照本文先前設定的預熱期和率定期進行模型率定，并忽略預熱期有關計算結果和方程，擬合結果如圖1所示。由圖1可知，二者在率定期和驗證期的擬合程度相對較好。對不同時期評價指標可采用SUFI- 2算法進行檢驗，檢驗結果見表3。研究結果表明，模型中參數指標精確度在不同時期均表現出良好的結果，符合模型模擬相關要求可進行下一步的模擬預測。

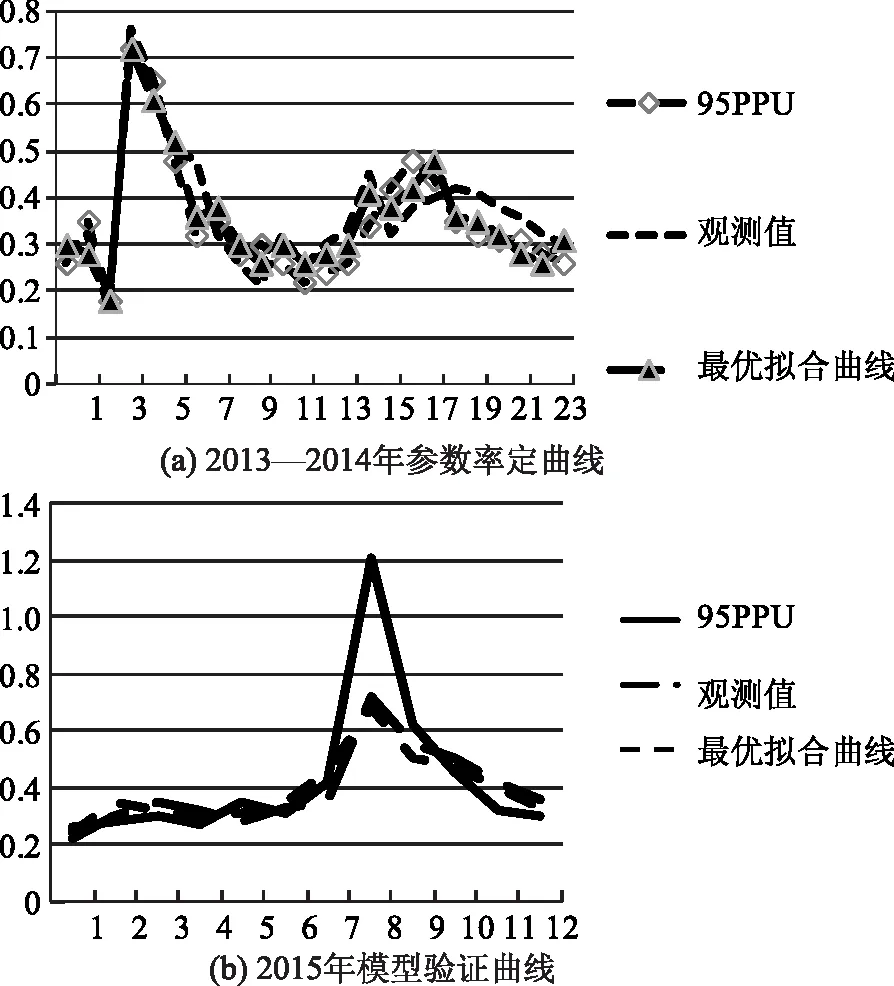
圖1 月徑流量觀測值與模擬值在率定期與驗證期擬合結果

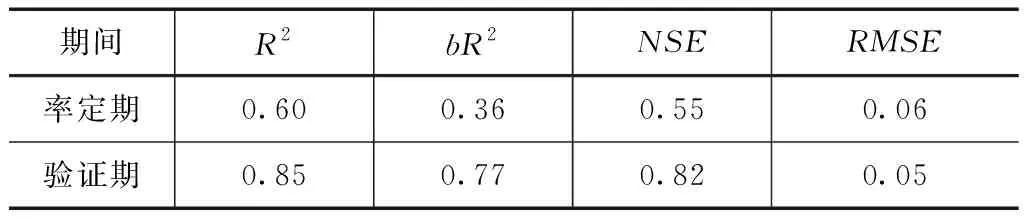
表3 遼陽水文站月徑流量模擬結果

3.3 不確定性分析

參數的取值區間可在一定程度上對參數不確定性產生顯著作用，如較小的取值范圍可提高模擬的置信水平并產生較窄的不確定性區間從而降低對變異的作用程度，大部分數據落在有效的區間以外。本文對R-faceot和P-factor進行求解，結果見表4。

表4 不確定性分析結果

其中置信區間為95%時的預期范圍符合本文中為2.5～97.5%范圍，而其低程度不確定性可由較大的R-faceot值進行確定，驗證期的0.06和率定期的0.08說明模型包含了52%和68%以上的觀測數據。在率定期和驗證期R-faceot分別為0.22和0.40，由此說明95PPU區間寬度較窄。

對每次模擬參數的取值依據SUFI- 2的散點圖進行分析，研究表明：不確定性的大小可依據散點的分布集中程度進行表征。結合橫坐標的范圍可對取值區間進行確定，而縱坐標的NSE值可按縱坐標范圍進行確定。0.5的閥值為紅線邊界值，置信水平與閥值以上分布點的多少呈正相關性即閥值以上散點越多則置信水平越高從而可知模型的不確定性越低。依據CANMX研究結果，0～1取值范圍可降低參數的不確定性，并且參數的可取值范圍變小從而引起參數的變異性降低。綜上所述，遼河流域遼陽水文站徑流模擬的不確定性整體處于較低水平[12]。

4 結論

本文以遼河流域為例進行水文過程模擬預測分析，并對模型的相關性能按照不同的參數進行研究分析，得出的主要結論如下。

(1)利用SWAT敏感性分析結果可對SUFI- 2參數敏感性進行分析，除了參數一次性全部輸入外其他各參數在初次輸入時均存在一定的盲目性。

(2)參數敏感名研究結果顯示，對模型徑流預測模擬影響最大的土壤，并且基流衰退常數以及SCS徑流曲線值具有一定的敏感性。

(3)遼河流域遼陽水文站在率定期與驗證期的觀測值與模擬值擬合程度處于較高水平，相對于率定期驗證期相對較大，其原因主要與參數驗證年份較少擬合較快等因素相關。