光纖陀螺隨機漂移的混沌特征分析

狄世彥，李 賀，朱奎寶，鄧學文

(中國航天科工集團第二研究院706所，北京 100854)

0 引 言

光纖陀螺隨機漂移可看作是一組具有非線性、非平穩和弱時變特性的隨機時間序列，這些特點限制了光纖陀螺向高精度領域的發展，因此，建立準確有效的隨機漂移模型并進行預測補償是有意義的。目前，時間序列的分析預測方法主要有兩種：一種是應用較早、發展較成熟的傳統統計建模方法，如自回歸模型(AR)和自回歸滑動平均模型(ARMA)[1,2]，這種方法要求時間序列必須是平穩的、正態分布的零均值序列，對于慢時變的陀螺信號，其模型的預測精度受到很大的限制；另一種是以神經網絡為代表的現代非線性預測模型，如人工神經網絡、小波分析、模糊邏輯等等，神經網絡可以很好地逼近非線性函數，但其遵循的經驗風險最小準則降低了算法的泛化能力，且易陷入局部最小值。本文研究的目的是找到一種泛化能力強、預測準確的光纖陀螺隨機漂移模型。

1 光纖陀螺隨機漂移的混沌特征

1.1 混沌運動

所謂混沌，是指在確定的非線性動力系統中存在的一種貌似隨機的運動。對于確定性動力系統，可由給定的初值推知系統未來的發展狀況，對于非線性系統，系統對初值相當敏感，即使初值有微小的變化，也將引起系統長期狀態的極大變化，如著名的“蝴蝶效應”。混沌是確定性系統內在隨機性的反映，它與受外部因素影響的隨機性不同，系統可用確定性的方程描述，在不附加任何其它隨機因素的情況下，系統仍會表現出一定的類似隨機行為。通常的隨機性由于不服從確定的動力學規律，其隨時間的發展是不可預測的，但混沌發生在確定性系統中，其服從一定的動力學規律，因此，混沌系統在短時間內是可以預測的。混沌理論最早來源于法國著名數學家Poincare在研究三大球體時提出的假設[3]，他意識到三大球體受到微小的干擾，將可能導致完全不一樣的運行軌道。1963年美國氣象學家Lorenz在研究大氣流動問題時發現了混沌現象，1975年華人學者李天巖和美國數學家York首次給出了混沌的數學定義，并證明：一個周期為3的軌道存在，則一定有混沌現象出現。

混沌運動客觀存在于自然界中，它是一種不規則的、非常復雜的運動形式，主要有以下幾個特征：

(1)長期運動對初始條件極為敏感

初始狀態非常靠近的兩個點，其軌道的差距隨著時間的推移會成指數擴大，這使得混沌系統的長期演化行為變得不可預測。

(2)相空間中存在奇異吸引子

吸引子是動力學過程的軌跡，在經過足夠長時間的發展之后，其將逐漸達到收斂的狀態或狀態的集合。動力系統有3類吸引子：平衡點、極限環河奇異吸引子，平衡點是系統運行軌跡收斂到一個不動點，極限環是系統軌跡呈現周期性，而混沌系統的奇異吸引子在軌道中表現出無限的扭曲和折疊。平衡點和極限環的維數常為整數，混沌吸引子由于是分形結構而具有分形維。

(3)內在隨機性

混沌系統隨機性的根源是來自確定性系統的內部，并不僅僅依賴于外部因素的干擾。

(4)標度不變性

混沌是一種無周期的有序，混沌系統的演化會出現分叉行為，并遵從Feigenbaum普適常數。

當今社會上的混沌現象無處不在，不同行業的學者都可以在自己的研究領域找到混沌現象，從20世紀90年代開始，混沌的研究已經開始在學科間相互滲透，無論是物理學、生理學、電子學，還是氣象學、經濟學、音樂，混沌理論都有著廣泛的應用。

1.2 光纖陀螺隨機漂移混沌特征的判定

時間序列是自然界中某一個或一組變量按時間先后和相同時間間隔排列的一組觀測數值，現實生活中如股市指數、地區降雨量、河流徑流量等都可看作是時間序列，這些序列均被發現含有混沌特性[4]。為了揭示混沌時間序列貌似隨機現象的背后可能隱藏的規律，需要采用時間序列分析方法來提取序列中含有的準確信息，并通過建立相應的數學模型來對時間序列的未來值進行預測，以給人們的生活帶來更多的幫助。

混沌運動來自于非線性動力學系統，這使得混沌時間序列具有非線性、非平穩的特征，因此，基于統計學理論的線性回歸模型預測方法對于混沌時間序列的預測是困難的，而基于數據的各種機器學習方法在混沌時間序列的預測中逐漸得到應用[5]。要采用混沌理論的相關知識對時間序列作出較為精確的預測，必須判斷時間序列是否具有混沌特性，常用的混沌時間序列判別方法主要有：功率譜法、Poincare截面法和最大Lyapunov指數法，其中最大Lyapunov指數法應用較多[6]。

混沌運動的一個基本特征是長期運動對初始條件非常敏感，極其相近的初值所運行的軌道，其差距會隨著時間的推移按指數形式擴大，而Lyapunov指數能夠定量描述出兩個軌道的發散特征。在識別混沌運動時，通常只需要計算最大Lyapunov指數λl即可，若λl為正，則表明系統運行軌道有發散特征，呈混沌運動；若λl為零，則表明系統運行軌道對初值不敏感，呈周期運動；若λl小于零，則系統的長期運行軌道與初值無關，系統運動軌跡最終將收斂到一個平衡點。

求取時間序列的最大Lyapunov指數λl的方法較多，常用的有雅克比法和Wolf軌線法[7,8]。Wolf法直接根據相軌線、相體積、相平面等的演化來估計Lyapunov指數，由于光纖陀螺隨機漂移可看作是非線性、非平穩的時間序列，因此，本文采用Wolf法來計算隨機漂移的最大Lyapunov指數。在相同的環境條件下，采集同一型號的8只光纖陀螺的常溫靜態數據，每只陀螺的采樣時間為3600 s，采樣間隔1 s，為了消除奇異點和部分噪聲的影響，計算前對采樣數據進行零偏補償和低通濾波去噪，如圖1所示為其中一組光纖陀螺隨機漂移的實驗數據。

圖1 預處理后的光纖陀螺隨機漂移

利用wolf法計算最大Lyapunov指數的主要過程如下：

任取一組光纖陀螺隨機漂移作為計算的時間序列{x(n),n=1,2,…,N}，N為數據長度，用嵌入維數m和延遲時間ττ對隨機漂移進行相空間重構(關于相空間重構的內容在后續章節介紹)，M是重構空間的相點個數，M=N-m-1，則重構空間中的相點可表示為

X(i)=[x(i),x(i+τ),…,x(i+(m-1)τ)]
i=1,2,…,N-(m-1)τ

(1)

(1)首先將重構空間中的相點X(i)作為一條基準軌線，并在基準軌線上選定一個初始點X(0)；

(2)然后在X(0)的鄰近范圍內選定另一個點，可得兩點間的距離向量L(0)，要求L(0)滿足L(0)<ε,ε為一大于0的閾值，且盡量使L(0)的方向與基準軌線在X(0)處的切向量不平行；

(3)追蹤這兩個點的演化，當經過一段時間后，L(0)變為L′(1),X(0)變為X(1)，如果L′(1)>ε,則在X(1)附近再選定另一個點，得到距離L(1)，滿足L(1)<ε；

(4)重復上述過程，可得一組L(k)以及L′(k)，用下式計算最大Lyapunov指數λl，K為總的迭代次數

(2)

運用上述方法所估計的8組光纖陀螺隨機漂移的最大Lyapunov指數見表1。

表1 光纖陀螺隨機漂移的最大Lyapunov指數

由表1可見，8組隨機漂移的最大Lyapunov指數的估計值均大于0，這說明光纖陀螺隨機漂移具有混沌特性，因此，采用混沌系統的相關模型對光纖陀螺隨機漂移進行預測是可行的。

2 光纖陀螺隨機漂移的相空間重構

2.1 相空間重構參數的計算

自然界和工程技術領域中的許多系統都是復雜的高維非線性系統，這些系統往往包含多個變量的信息，但通常情況下只能觀測到系統的一維信息，即某一分量的時間序列。由于系統任一分量的演化是與其它分量相互作用的結果，這些相關分量的信息蘊含在任一分量之中，因此，從某一個分量的時間序列中就可以提取和恢復出系統內在的規律。相空間重構(phase space reconstruction，PSR)是找出數據隱藏演化規律的重要方法，是分析混沌系統的主要工具，其目的是將一維的時間序列通過重構的方式嵌入到多維相空間中，從而恢復出系統的吸引子。

Packard等于1980年提出了相空間重構理論以及廣泛使用的時間延遲相空間重構方法[9]，1981年Takens從數學角度證明了相空間重構的方法[10]。時間延遲重構法的基本思路如式(1)所示，Takens已經給出證明，當嵌入維數m≥2d+1(d是動力系統的維數)時，重構的相空間是一個嵌入映射，它能夠保存非線性動力系統的許多特征，并在拓撲等價下恢復出這些特征。

前一節中已經通過計算最大Lyapunov指數證明了光纖陀螺隨機漂移存在混沌特性，但一維的光纖陀螺隨機漂移時間序列無法表現出系統的隱藏演化規律。因此，本文借助于相空間重構技術將一維的隨機漂移時間序列嵌入到高維空間中，在高維空間中對隨機漂移數據進行回歸分析與預測。相空間重構的關鍵問題是如何正確選擇嵌入空間維數m和延遲時間τ，m太小難以展示出系統的實際結構，m太大使得相點之間的關系變得模糊，增加了計算的復雜度。對于有限的數據，恰當的τ很重要，τ太小，則重構空間的相點相關性太強，系統信息無法完全顯露，τ太大，則動力系統可能失真。

目前，計算嵌入維數m和延遲時間τ最常用的方法是由Kim等于1999年提出的C-C算法[11,12]，這種方法認為兩個參數是相互關聯的，其取值相互依賴，并通過引入嵌入窗τw=m-1τ[13]將m和τ聯系起來。由于C-C算法相對簡單，計算量小，有較好的抗噪聲能力，本文應用C-C法計算光纖陀螺隨機漂移的兩個相空間重構參數，計算的主要過程如下：

選取1.2節中的一組光纖陀螺隨機漂移數據作為計算的時間序列xn,n=1,2,…,N，以嵌入維數m和延遲時間τ對其進行相空間重構，X(i)為重構空間中的一個點，則嵌入時間序列的關聯積分為

(3)

(4)

關聯積分是個累積函數，表示相空間中任意兩點間的距離小于r的概率，點間距離用向量差的無窮范數表示，定義檢驗的統計量

S(m,N,r,τ)=C(m,N,r,τ)-Cm(1,N,r,τ)

(5)

上式的計算方法為：將時間序列劃分成τ個相互不重疊的子序列，子序列的長度為INT(N/τ)，計算每個子序列的統計量

(6)

令N→∞，有

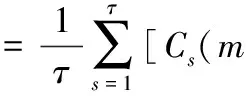
(7)

如果時間序列滿足獨立同分布，那么對于固定的m和τ，對于一切r，均有

(8)

由于實際的時間序列是有限的，且時間序列各數據之間可能存在相關性，Sm,r,τ一般不為0。當m和r固定時，Sm,r,τ～τ曲線反映了時間序列的自相關性，最優延遲時間τ取Sm,r,τ～τ第一次過零點時對應的時間。此外，選擇對應值最大和最小的兩個半徑r，定義差量

ΔS(m,τ)=max{S(m,rj,τ)}-min{S(m,rj,τ)}

(9)

當最大偏差ΔSm,τ最小時，重構的相空間點最接近均勻分布，重構的動力系統軌道最準確。由于ΔSm,τ為正數，最優延遲時間τ可取ΔSm,τ～τ的第一個局部極小值所對應的時間。

根據BDS統計的結論，當N≥3000，2≤m≤5，0.5σ≤r≤2σ時，Sm,r,τ～τ曲線能較好地表現出時間序列的自相關特性，σ為時間序列標準差，實際計算中取m=2,3,4,5,r=0.5σ,σ,1.5σ,2σ, τ∈0,20，并按下列各式計算

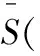
(10)

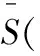
(11)

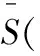
(12)

τw=(m-1)τ

(13)

圖2 C-C法計算隨機漂移的相空間重構參數

2.2 重構的相空間圖分析

為了從視覺上更加直觀地看到光纖陀螺隨機漂移所具有的混沌特征，可以根據C-C算法估計的最佳延遲時間τ=3作出光纖陀螺隨機漂移時間序列的相空間圖來進行定性分析，這里將隨機漂移時間序列的xt+τ值作為xt的函數畫在二維空間圖中，如圖3(a)所示。為了與隨機漂移的相空間圖作對比，用Matlab的rand函數在區間(0，1)內隨機產生3600個數據，并將隨機數時間序列的相空間圖同樣按延遲時間τ=3畫在二維空間圖中，如圖3(b)所示。

圖3 時間序列的相空間

由圖3可見，光纖陀螺隨機漂移時間序列的相空間圖與隨機數時間序列的相空間圖在直觀上存在著明顯的差異：隨機漂移時間序列的所有點在相空間圖中緊緊糾纏在一起，形成一個近似的圓形，且圖面僅占據二維圖中間的一部分，而隨機數時間序列的所有點在相空間圖中均勻分布，幾乎填滿了整個取值空間。光纖陀螺隨機漂移時間序列的相空間圖所具有的復雜形狀，與隨機數時間序列的相空間圖完全不同，兩者存在本質上的差別。由此可以推斷，光纖陀螺隨機漂移時間序列存在混沌特征，這與1.2節中計算的最大Lyapunov指數值所表征的結果相一致。

對光纖陀螺隨機漂移進行相空間重構的目的是為了將一維的標量時間序列重構成體現系統特征的高維空間向量，這些向量與現代非線性預測模型相結合，可以對光纖陀螺隨機漂移進行回歸分析與預測。

3 結束語

本文介紹了混沌運動的相關知識，并通過計算最大Lyapunov指數驗證了光纖陀螺隨機漂移所具有的混沌特性。為了有效地提取出隨機漂移的混沌特征，本文使用相空間重構的方法將一維的隨機漂移時間序列嵌入到一個高維的輔助空間中，重構參數由C-C法計算得到，根據相空間重構的參數繪制了隨機漂移時間序列和隨機數時間序列的相空間圖，兩種圖形存在的較大差異進一步說明了光纖陀螺隨機漂移存在的混沌特征。