簡單循環約減三三組合測試用例生成方法

艾 華，宋曉秋，安 恒

(中國航天科工集團第二研究院706所，北京 100854)

0 引 言

軟件測試在軟件開發過程中占重要地位，而測試用例是進行軟件測試工作的基石[1]，研究結果表明覆蓋強度為n的最小測試用例集生成問題是NPC問題，隨著參數數量的增多，測試用例集規模也成倍增長，覆蓋所有的組合勢必使得測試用例集過大，從而導致測試工作占用巨大花費，研究發現約70%的軟件缺陷可以通過兩兩組合測試發現，而通過三三組合測試能發現90%的軟件缺陷，最后可以通過六六組合測試發現幾乎所有的軟件缺陷。隨著覆蓋強度的增加，測試用例集規模成指數形式增長，因此研究人員在如何覆蓋強度為2的最小測試用例集的問題上進行了大量的研究，從不同角度出發提出了多種算法[2,3]。

迄今為止，軟件測試領域對兩兩組合測試已有充分的研究，而針對三三組合測試用例集的生成方法研究較少，主要包括IPOG算法、ITCH算法、Jenny算法等由兩兩組合測試算法改進而來的通用算法，以及王小銀等提出的基于蟻群算法的三三組合測試用例集的生成方法[4]。三三組合測試能彌補兩兩組合測試缺陷發現率較低的不足，還能避免更高覆蓋強度組合測試成本過大的問題，本文以貪心算法為基礎[5]，借鑒IPO算法的思路，針對三三組合測試問題，提出了一種簡單循環約減三三組合測試用例生成方法(simple-cyclic-reduce，SCR)，算法的基本思路是先找到取值最少的前3個參數形成的最小測試用例集，再對剩下的參數進行逐個擴展，在擴展的同時進行循環約減，尋找當前已擴展參數的局部最優解[6]，直到參數完全擴展，得到的解近似代替全局最優解[7]。

1 組合測試概念及其模型

假定待測系統SUT(software under testing)有n個輸入參數，用集合X={x1,x2,x3,…,xn}表示，輸入參數xi對應的值域為Yi(i=1,2,3,…,n)。

定義1 測試用例集：假定某集合Ts={t1,t2,t3,…,tn}，對于集合中任意元素ti∈Ts,ti={ti1,ti2,ti3,…,tin},且tij∈Yj(i=1,2,3,…,n;j=1,2,3,…,n;i,j不相等)，則稱集合Ts為待測系統SUT的一個測試用例集，ti為待測系統的一個測試用例。

定義2 兩兩組合測試用例集：假定某集合Ts為待測系統SUT的一個測試用例集，如果集合X中任意兩個不同參數組成的任意組合對(xi,xj)，滿足如下條件，存在t∈Ts，使得任意xi∈t,xj∈t(其中i=1,2,3,…,n;j=1,2,3,…,n，i,j不相等)，則稱Ts為待測系統SUT的一個兩兩組合測試用例集。

例：設待測系統SUT有3個輸入參數{x1,x2,x3}，各參數對應的值域{a,b}、{c,d}、{e,f},則SUT共有12個兩兩組合對，見表1。

覆蓋這些兩兩組合對至少需要4個測試用例：(a,c,e)、(a,d,f)、(b,c,f)、(b,d,e)。兩兩組合測試能保證由一個參數及兩個參數間相互作用引發的軟件缺陷能被發現。

表1 3個2值參數SUT的兩兩組合對

定義3 三三組合測試用例集：假定某集合Ts為待測系統SUT的一個測試用例集，如果集合X中任意3個不同參數組成的任意組合對(xi,xj,xk)，滿足如下條件，存在t∈Ts，使得任意xi∈t,xj∈t,xk∈t(其中i=1,2,3,…n;j=1,2,3,…n;k=1,2,3,…n;i,j,k互不相等)，則稱Ts為待測系統SUT的一個三三組合測試用例集。

例：設待測系統SUT有4個輸入參數{x1,x2,x3,x4}，各參數對應的取值{a,b}、{c,d}、{e,f}、{g,h},則SUT共有32個三三組合對，見表2。

覆蓋這些三三組合對至少需要8個測試用例(a,c,e,g)、(a,c,f,g)、(a,d,f,g)、(b,c,f,g)、(a,d,e,h)、(b,d,e,g)、(b,c,e,h)、(b,d,f,h)。三三組合測試能保證到一個參數、兩個參數及3個參數間相互作用引發的軟件缺陷能被發現。

表2 4個2值參數SUT的三三組合對

2 相關研究

通過幾十年的研究與積累，在組合測試用例集生成的研究中，兩兩組合測試用例集的研究已經相當充分，相關的算法有很多，其中較為常見的有基于代數構造法的正交拉丁方技術，及其變種Williams算法和Kobayashi算法；有基于貪心算法的IPO算法、AETG算法等；有基于解空間樹的PSST算法；有基于蟻群算法的ACO算法，以及在這些算法的基礎之上進行的通用化研究，將這些算法中的部分算法擴展到了三三組合測試用例集生成甚至n-way組合測試用例集生成，以下介紹幾種常用的組合測試用例生成算法。

2.1 AETG算法簡介

Cohen等提出通過“one-test-at-a-time”的思想來構建測試用例集直到所有的兩兩組合對都被覆蓋的AETG算法，AETG算法在構建測試用例時采用盡可能多地覆蓋較多的未覆蓋組合對的貪心策略來生成較小的測試用例集。最初AETG算法旨在生成兩兩組合測試用的組合測試用例集，隨著AETG算法的豐富與發展，出現了較多以AETG算法為基礎的變種以及通用的組合測試用例生成方法。

2.2 IPO算法簡介

Yu Lei等提出了生成結對測試用例的IPO算法，IPO算法采用貪心算法依次對參數進行水平擴展和垂直擴展直到擴展完所有的參數。IPO算法的基本思想是先對所有參數按照取值域非遞增排序，先用前兩個參數構造初始測試用例集，再依此進行水平擴展和垂直擴展，水平擴展在測試用例數量不變的基礎上，添加新的參數的取值，使之包含的未覆蓋組合對數量最多；垂直擴展在參數數量不變的基礎上，增加新測試用例使得包含的未覆蓋組合數量較多，或者改變已有的測試用例來實現覆蓋，直到所有組合對都被覆蓋，再擴展下一個參數，直到所有的參數都擴展完成。

同樣地IPO算法最初也是解決兩兩組合測試的測試用例集生成問題，Yu Lei等對IPO算法進行通用化改進，提出IPOG算法和IPOG-D算法，使得該算法能解決n-way(2≤n≤6)組合測試用例集生成問題。IPOG算法整體與IPO算法相似，在初始化測試用例集所用參數個數以及組合對的覆蓋強度上有變化，IPOG-D算法改變了擴展方式，將參數分為兩組采用遞歸的形式進行求解，水平擴展過程是直接將列復制的過程，垂直擴展是將兩種覆蓋強度的組合合并的過程，結果往往比IPOG算法差，但節省了遍歷并判斷所有的n-way組合對是否被覆蓋的時間，速度方面比IPOG算法快。

2.3 ACO算法簡介

王小銀等提出了基于蟻群算法的解決思路(ant colony optimization，ACO)，和AETG算法一樣，采用“one-test-at-a-time”的思想來逐個測試用例地生成組合測試用例集。在蟻群搜索組合測試用例生成過程中，將參數對應成節點，參數的取值對應為從節點引出的有向邊，一個測試用例為經過各節點的一條路徑。蟻群算法過程是先將所有的螞蟻匯集在出第一個節點，然后每只螞蟻根據當前節點各邊的信息素和動態啟發信息的概率來選擇到下一節點的邊，直到螞蟻走完所有節點，此路徑對應一條測試用例，并添加到測試用例集中，直到覆蓋所有的三三組合對。

2.4 算法比較與工具介紹

AETG算法每次生成測試用例時都會產生M個候選的測試用例，Cohen通過實驗驗證M=50時，算法的時間花費和結果相對較好，但總體時間花費較大。IPO算法直接對參數進行擴展，每次擴展一個參數，生成測試用例的速度快，但局部尋優能力有限，產生的結果往往不如AETG算法。ACO算法將蟻群算法的思路應用到測試用例集的生成問題上，但該算法信息素計算過程復雜，產生的結果有局限。目前三三組合測試方面的研究相對較少，逐參數擴展方面還有待改進，本文就此進行了研究。

Bob Jenkins在用C語言寫了基于貪心算法的Jenny工具并公布在個人網站上供測試人員研究，此工具能生成2～6-way的測試用例集，Jenny工具操作簡單，無界面，能直接輸入參數調用并返回測試用例集。IBM研究院綜合幾種代數方法用Java語言設計了ITCH(intelligent test case handler)工具。Yu Lei用Java語言實現了IPOG算法和IPOG-D算法等多種逐參數形式生成測試用例集的策略，開發了具有用戶界面的ACTS工具，ACTS工具可操作性強，能選擇不同策略，不同覆蓋強度以及制定參數間的約束，生成測試用例集后還可以驗證組合對的覆蓋率。

3 SCR算法

SCR算法以貪心算法為基礎，根據逐參數擴展的思想來逐步生成三三組合測試用例集[8]。先從參數集中選擇取值最少的前3個參數生成一個初始測試用例集，初始測試用例集包含所選3個參數的所有取值組合，接著向測試用例集中添加第4個參數，在添加參數時，利用該參數的所有取值[9]對測試用例集中所有的測試用例進行直接擴展，最后再對測試用例集中所有測試用例進行循環約減，直到循環約減測試用例集前后測試用例的數量不變，再添加下一參數，重復直接擴展和循環約減過程，直到擴展完所有參數[10]。

直接擴展過程：在增加參數時對當前測試用例集的所有測試用例，直接利用待擴展參數的所有取值對測試用例集的所有測試用例逐一擴展，使得新的測試用例包含的參數個數比之前的測試用例多一個。

直接擴展保證了完全覆蓋性，增加參數時利用該參數的所有取值情況對上一步得到的測試用例集逐一擴展，擴展該參數后，由已擴展參數組成的所有三三組合對均包含在測試用例集中，而且測試用例之間可能重復包含部分三三組合對，因此需要再進行循環約減過程來進一步找到局部最小測試用例集。

循環約減過程：直接擴展后的測試用例集中可能存在大量可以約減的測試用例，判斷測試用例能否約減的依據是該測試用例包含的所有三三組合對是否都被其它測試用例包含。遍歷直接擴展后得到的測試用例集中的每個測試用例，若可以約減則從測試用例集中刪除，循環上述過程，直到循環前后測試用例集大小不變[11]。

循環約減保證了局部最優性，每次循環約減后的測試用例集是包含已擴展參數的局部最優解，并作為擴展下一個參數的初始測試用例集，重復以上過程當擴展完所有參數并循環約減后得到的測試用例集即為全局近似的最優解。

如圖1所示，SCR算法求解過程中需要輸入參數集X={x1,x2,…,xn}， X含有n個參數(n不小于3)，SCR算法輸出測試用例集Ts。

圖2舉例說明了SCR算法求解4個2值參數SUT的具體過程，以下將結合SCR算法描述具體分析求解過程，以便進一步說明SCR算法的基本思路。

圖1 SCR算法描述

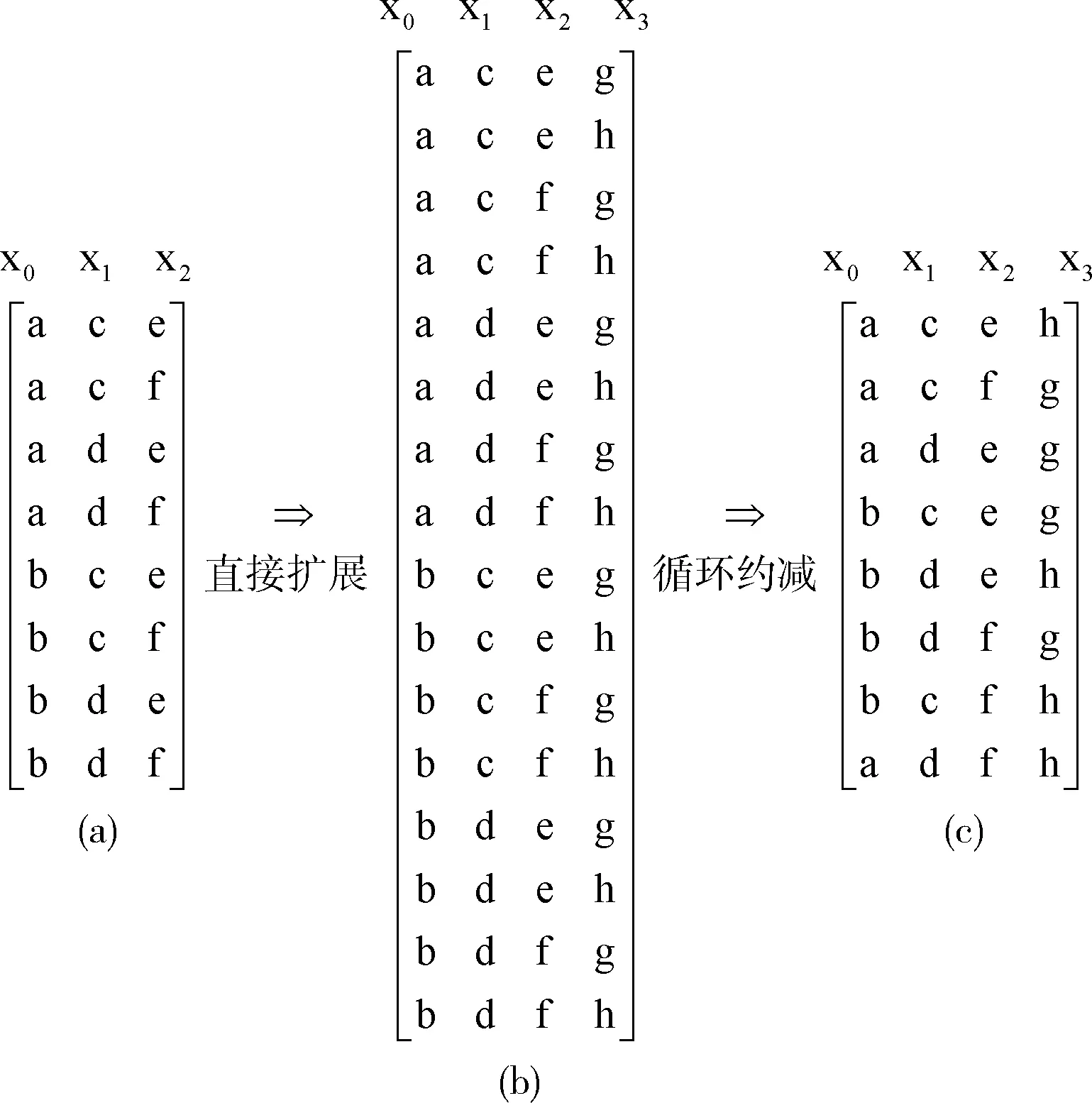
圖2 SCR算法求解4個2值參數SUT過程

算法首先將測試用例集Ts初始化為空(line 1)，在調整參數集X順序,使得X中前3個參數的取值數最少(line 2)，并利用X中前3個參數x1、x2、x3的所有組合加入Ts(line 3)，得到的結果如圖2(a)所示。

接著在Ts中的每個測試用例添加x4，使之擴展成新的Ts(lines 6-11)，因為x4有兩種取值，此前Ts規模為8，故擴展之后的Ts包含16個測試用例。對于第一個測試用例(a,c,e)，應該擴展為(a,c,e,*)，因為x4可以是g或h，故(a,c,e)被擴展為(a,c,e,g)和(a,c,e,h)，將擴展后的測試用例添加到Ts，并將被擴展的測試用例刪除，得到最終的結果如圖2(b)所示。

最后循環約減Ts，遍歷直接擴展后的Ts中所有的測試用例t(line 18)，如果t中是否包含只有t覆蓋的三三組合對，則t不可約減，Ts不變(line 22)，否則t可約減，將t從Ts中刪除(line 24)，循環對Ts進行約減處理，直到在約減前后Ts中測試用例數量不減少(line 16)。對于第一條測試用例(a,c,e,g),包含的三三組合對有(a,c,e)、(a,c,g)、(a,e,g)、(c,e,g)，而這些三三組合還分別被Ts中測試用例(a,c,e,h)、(a,c,f,g)、(a,d,e,g)、(b,c,e,g)包含，因此測試用例(a,c,e,g)可以被約減。對Ts中每個測試用例重復第一條測試用例的操作，可知(a,c,e,g)、(a,c,f,h)、(a,d,e,h)、(a,d,f,g)、(b,c,e,h)、(b,c,f,g)、(b,c,f,h)、(b,d,e,g)、(b,d,f,h)均可被約減，且此時Ts中的測試用例都不能被約減，即循環約減結束，則最終得到的結果如圖2(c)所示。

4 實驗驗證

SCR算法使用貪心策略逐個地尋找局部最優解，在尋找添加下一個待擴展參數之后的局部最優解時，以當前局部最優解為基礎，并利用待擴展參數的所有取值直接擴展，再循環約減得到添加下一個參數之后的局部最優解，直到找到所有參數都被擴展后的局部最優解，這個局部最優解近似地代替全局最優解。

本文最后通過Java編程語言在Eclipse編程工具下實現了SCR算法[12]，在搭載了Intel(R) Core(TM) i5-7500 處理器，8G內存的64位Windows 10的操作系統的臺式機上進行了如下實驗，為充分比較算法的有效性，還從http://ranger.uta.edu/～ylei/fireeye/下載了FireEye開源工具，FireEye工具實現了IPOG算法等多種逐參數擴展的方法，FireEye工具重新命名為ACTS，以下實驗中用ACTS來進行表示。此外還有C語言編寫的開源工具Jenny，同樣地，從http://www.burtleburtle.net./bob/math/jenny.html下載了Jenny工具進行實驗比較。

表3和圖3展示了具有3～10個2值參數的SUT，SCR算法生成的結果規模與時耗，含有3個或3個以上的2值參數的系統滿足三三覆蓋的測試用例數量至少是23=8，因此在表3中3個、4個參數的系統的最終解即最優解，隨著參數個數的增加，最終解偏離了最優解，但隨著參數個數的增加，測試用例數量增加慢，測試用例的增長趨勢大致成線性趨勢增長，而不是指數趨勢增長。

表4和圖4展示了具有4個2值到7值參數的SUT，SCR算法生成的結果規模與時耗，含有3個或3個以上的2值參數系統滿足三三覆蓋的測試用例數量至少是23=8，在表4中4個2值參數的最終解即最優解，隨著參數取值個數的增加，最終解偏離了最優解，隨著參數個數的增加，測試用例數量增加較快，測試用例的增長趨勢大致成指數趨勢增長。

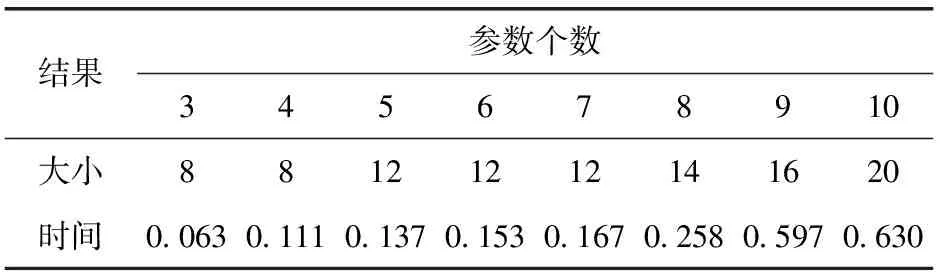
表3 3～10個2值參數結果

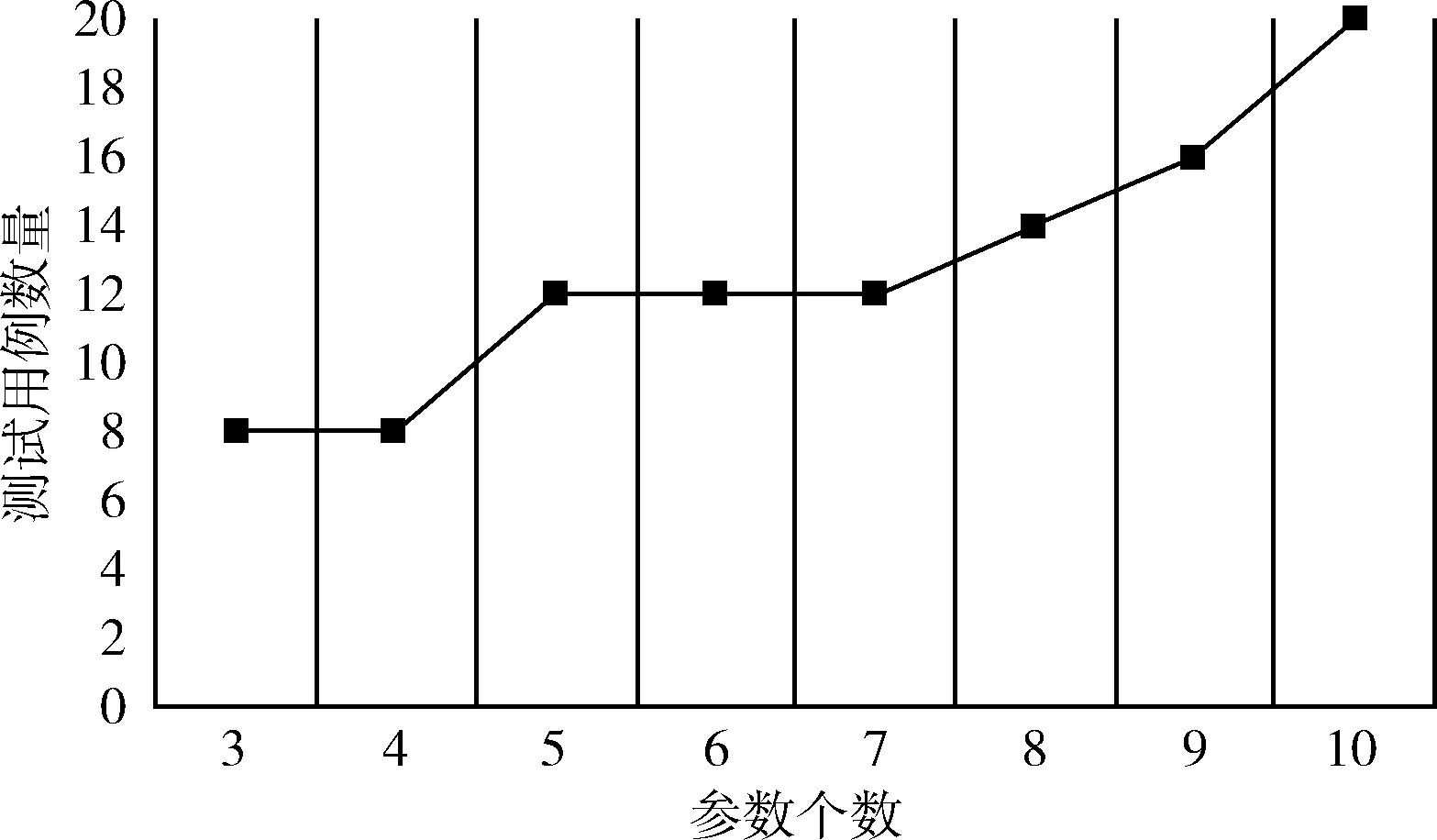
圖3 測試用例數量與2值參數個數曲線

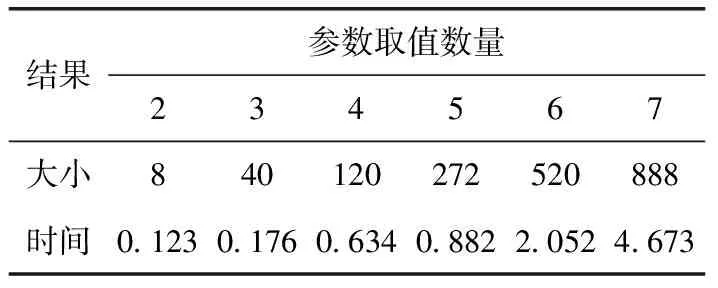
結果參數取值數量234567大小840120272520888時間0.1230.1760.6340.8822.0524.673

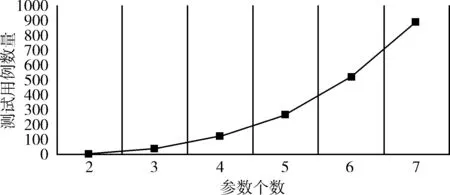
圖4 測試用例數量與參數取值個數曲線

表5和圖5展示了具有5-15個5值參數的SUT，SCR算法和基于蟻群算法的ACO算法結果規模的比較，ACO算法在求解過程中利用信息素能迅速得到結果，SCR算法采用循環約減的方式運行時間長，測試用例集規模小。

表5 5～15個5值參數生成結果比較

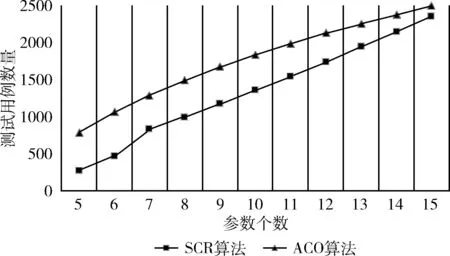
圖5 SCR算法與ACO算法比較

表6展示了不同系統下各種算法的結果，其中工具ACTS有多種策略，對于此實驗，IPOG算法生成結果較好，選擇ACTS中IPOG算法生成的結果進行比較(實驗系統：25314151表示5個2值參數，1個3值參數，1個4值參數和1個5值參數組成的系統)。

綜合以上結果，可以看出SCR算法生成的三三組合測試用例集規模小，且方法簡單只包含直接擴展和循環約減的過程，能逐個添加參數并輸出測試用例，隨著參數的增多測試用例集規模變大，在測試時可以給測試人員提供參考，根據測試成本與測試需求選擇合理的參數規模。

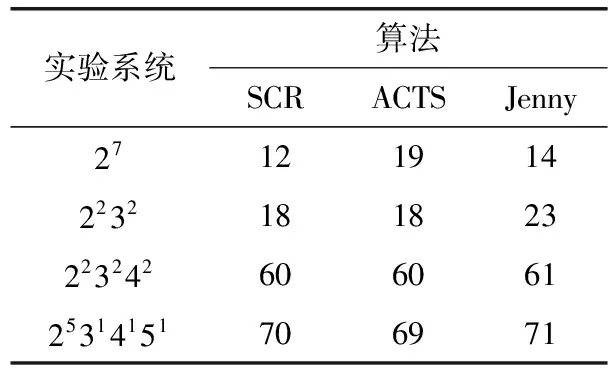
表6 3種方式生成的結果比較

5 結束語

本文提出了以貪心算法為基礎，逐參數生成測試用例的簡單循環約減的三三組合測試用例生成算法(SCR算法)。此方法先生成包含3個參數的最小測試用例集，再進行直接擴展和循環約減，得到最終結果。使用直接擴展和循環約減的方式生成測試用例集，方法簡單，結果較好，能輸出每次添加待擴展參數的之后用例集，運行時間比基于蟻群的三三組合測試用例集的生成方法和IPOG方法長。此外，SCR算法在求解過程中，參數的順序不同會導致結果有顯著的差異，因此SCR算法的時間復雜度和參數排序方面有待進一步研究。