翻轉課堂在高中數學中的教學實踐研究
——以“等比數列及其通項公式”的教學實施為例

魏躍先

（甘肅省莊浪縣第四中學，甘肅 莊浪）

翻轉課堂是當下教學模式中比較能得到人們認可的一種教學模式，已經運用于多種教育領域。翻轉課堂其本質仍然屬于面授式的教學方式。課堂上老師可以采用多種技術實施教學過程，落實教學目標。具體而言，就是重新調整了課堂內外的組織結構和分配時間，把學習的主動權還給學生。這種模式的優勢明顯，學生可以有效地利用有限的時間并取得良好的學習效果。下面以高中數學“等比數列及其通項公式”的實施為例，談翻轉課堂在高中數學中的教學實踐效果。

一、教學設計思路

本節是人教版高中數學必修五第二章第四節的內容，“等比數列及其通項公式”在教材中的作用特殊，教學環節上承前啟后。既是對前面等差數列相關知識的鞏固，又奠定了后面等比數列的前n項和相關內容的學習基礎。它是一個生活化的數學問題，學好本節內容能夠培養學生學以致用的能力，同時也能讓學生達到知識遷移的目的。

二、教學目標

1.掌握等比數列的概念

2.理解等比數列通項公式的推導過程，熟練掌握并運用

三、教學重難點

等比數列通項公式的推導過程

四、教學技術的運用

錄制微課視頻，配合視頻準備學案，并設置探究的問題。

五、課前準備環節

提前讓學生在有條件的地方看微視頻內容，老師準備配套的學案，這是非常重要的一個環節，是學生整個活動的“路線引導圖”。老師只是個引路者，應讓學生按照“路線圖”自主學習。

等比數列及其通項公式學案：

（1）等比數列的定義

【定義】如果一個數列從第2項起，每一項與它的前一項的比等于同一個常數，這個數列就叫做等比數列。這個常數叫做等比數列的公比，公比通常用字母q表示（q≠0）。注：q=1時，an為常數列。

【舉例】請同學們列舉一個等比數列，說出它的公比是多少？

（2）等比數列的通項公式

如何推導等比通項公式呢？設等比數列{an}的公比為q，

此時用歸納法來推導：

q=1時單獨討論；

當q≠1時，

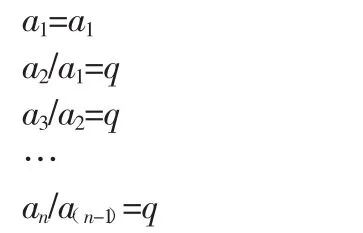
將這n個式子相乘后左邊只有一個an

結果是：an=a1*q^（n--1）

等差數列的通項公式可以利用累加法進行證明，請類比利用累乘法推導出等比數列的通項公式。

（3）等比中項

【定義】等比中項:如果在a與b中間插入一個數G，使a，G，b成等比數列，那么稱這個數G稱為a與b的________________，即G=__________________.

即，若 ______________________，則 a，G，b 成等比數列。

【探究】若a，b兩數存在等比中項G，則a，b必須滿足什么條件？

六、教學過程

一般來說，一節課就是一個檢測、落實并能夠運用課前所學知識的過程，教師應根據學生在課前掌握的情況來安排本節內容的教學。因此，內容安排上要給學生留下一定時間來交流并分享自己的預習結果，在自測卷中，最后一題是大多數學生沒有完成的，課堂上可通過小組合作的方式，讓學生互相探究來完成。因為已經有了課前的預習，所以老師可以放手讓學生進行探究，老師只起引導的作用。

【探究活動】

（1）一種計算機病毒可以查找計算機中的地址簿，通過郵件傳播。病毒制造者從計算機把病毒傳播給第一輪的被感染計算機，假設每一輪每一臺計算機都感染20臺計算機，那么在不重復的情況下，n輪傳播后感染的計算機數量是多少。

（2）所謂的“利滾利”即把前一期的利息和本金加在一起算作本金，再計算下一期的利息。按照“利滾利”計算本利和的公式是：本利和=本金×（1+利率）存期。現在存入銀行2000元錢，年利率是2.58%，那么，按照復利，則年份和該年的本加利存在什么樣的數學關系？

（3）拉面是中國的傳統美食，一碗拉面至少需要256根面條，請問廚師從一根開始拉需要拉幾次才能拉夠一碗面？

三個探究問題在學生預習的基礎上利用教學中間環節拋出，學生的探究目的明確。學生分組進行探究，完成后進行心得交流，分享成果。老師引導提示學生找出首項和公比，并強化概念，這樣鍛煉了學生利用所學知識解決實際問題的能力。最后，老師進行總結，引導學生回顧等比數列通項公式的數學表達式，引出下面的探究活動。

本節內容的教學就是運用了翻轉課堂的教學模式，老師在設計好的一個又一個的探究問題的基礎之上，帶領學生深入理解等比數列通項公式。探究形式多樣，既有自主形式，又有合作形式。利用翻轉課堂模式進行教學的時候環節必須齊全，前后內容應環環相扣。

七、教學反思

本節教學內容運用了翻轉課堂的教學模式，重點要做好課前環節，給學生準備好視頻、學案、檢測卷，讓學生能夠自主完成預習。

本課教學內容的重點是讓學生能夠對等比數列的定義理解并掌握，對等比數列通項公式的推導要在實際中學會運用。

根據布魯姆的掌握學習理論，教師應在教學過程中應該給學生留下足夠的時間，本節內容翻轉課堂的實施，學生的自主時間還是比較充裕的。課中環節中有部分學生因為預習不充分，參與度不高，在小組學習中沒有融入其中，影響了學習效果。因此，在后續內容的教學中教師一定要重視這種情況的發生。