永磁電機驅動的刮板輸送機主傳動系統機電耦合扭振動態分岔研究

鞠錦勇， 李 威， 范孟豹, 王禹橋， 楊雪鋒

(1.中國礦業大學 機電工程學院，江蘇 徐州 221116； 2.安徽工程大學 機械與汽車工程學院，安徽 蕪湖 241000)

近些年來，在國家“去產能”和“調結構”的宏觀調控下，確保煤礦開采的安全性以及高產高效變成了其首要任務[1]。現階段，傳統的刮板輸送機傳動系統為了實現軟啟動以及具有較強的過載能力，在異步電機和減速器之間增加液力偶合器、限矩摩擦離合器、調速偶合器等軟啟動裝備，這類機電傳動方式傳動線路長，傳動環節多，很容易出現諸多故障，并且齒輪傳動系統還需保證良好的潤滑[2-3]。在高效率、高可靠性以及大功率的發展趨勢下，傳統的異步電機驅動系統面臨著不少挑戰[4]。

在國家節能減排號召下，“變頻永磁直驅”成為各行業重點攻克的新課題[5-7]。隨著矢量控制和直接轉矩控制在交流調速系統中的不斷發展和完善，近年來在風力發電[8-9]、裝備制造[10-11]、電動汽車[12-13]、船舶推進[14]、礦業牽引等傳統采用異步電機的領域不斷可見交流永磁電機的應用。Haring等[15]指出交流永磁電機在很寬的速度范圍內具有高的響應性能和靈活性，使得永磁直驅概念對于大部分的實際應用是可行的。采用大功率永磁電機直接驅動工作裝置，實現 “近零傳動”，能夠顯著提高系統運行效率以及降低故障率，是現今大功率機電裝備的發展趨勢[16]。但是，由于刮板輸送機主傳動系統(機頭)是一個多質量彈性連接的機械動力學系統，在運輸作業時所施加負載力矩和電動機電磁轉矩的聯合作用下，將使系統連接軸產生扭轉振動。并且采用大功率永磁電機直接驅動刮板輸送機機頭滾筒，省去了中間傳動機構，系統連接軸所承擔的電磁轉矩與負載力矩將會顯著變大，其扭轉振動現象將更加明顯[17-18]。因此為了確保大功率永磁電機在刮板輸送機上的安全可靠運用，首先需要對刮板輸送機主傳動系統扭轉動態特性進行分析。

在分析刮板輸送機主傳動軸系這類相對轉動運動系統時，多數學者將其等效為質量彈性扭轉系統。Duan等[19]對含摩擦、間隙和裂紋的轉子系統研究時發現系統出現亞臨界Hopf分岔是導致主傳動系統發生自激振動的主要原因；劉彬等[20]將軋機主傳動系統等效為轉子-軸承相對轉動系統，并基于非線性反饋控制對系統分岔進行了控制；劉爽等[21]考慮時滯非線性參數的影響，分析了一類相對轉動系統的Hopf分岔特性；Das等[22]采用多尺度法分析了一類柔性轉子-軸承相對轉動運動系統的扭轉振動特性，并提出通過控制電磁驅動器以提高系統臨界轉速。上述研究較好地從機械參數角度，研究了摩擦、間隙、外部負載等因素對相對轉動運動系統扭轉動態特性的影響，但是忽略了電氣系統對系統動態特性的影響。由于永磁電機作為整個系統的直接動力源，其輸出電磁轉矩直接作用在相對轉動系統連接軸上，必然對系統連接軸動態特性產生較大影響。孟杰等[23]基于機電系統分析動力學，對高速電主軸電機-主軸系統進行了局部耦合和全局耦合分析，并據此分析了該系統的機電耦合動力學特性；熊萬里等[24]建立了異步電機-轉子系統的機電耦合模型，并采用數值計算研究了負載波動及串聯補償電容引起的系統機電耦合非平穩過渡過程；Kia等[25]分析了一類感應電機-變速箱機電系統，討論了齒輪箱軸系扭振對感應電機電流及轉矩的影響；田擁勝等[26]針對一臺高速永磁電機設計了電磁軸承轉子系統，并對該系統進行了動力學性能分析與實驗測試研究。但是由于機械參數與電氣參數之間復雜的非線性耦合關系，上述研究主要是通過數值仿真進行分析，對于電機系統與相對轉動轉子系統的機電耦合特性還有待進一步深入研究，從而有利于相對轉動系統的安全平穩運行。

本文以交流永磁電機驅動的刮板輸送機主傳動系統為研究對象，考慮刮板輸送機作業過程中運輸煤物料質量不均勻性產生的非線性摩阻，基于拉格朗日-麥克斯韋原理[27]，建立了刮板輸送機主傳動系統機電耦合非線性扭振動力學模型，研究非線性摩阻轉矩系數變化時系統表現的復雜動力學行為，重點分析系統的Hopf分岔形式及運動穩定性。這對大功率永磁電機在刮板輸送機上的有效利用，以及刮板輸送機主傳動系統的安全穩定運動具有非常重要的意義。

1 系統機電耦合動力學建模

構成永磁電機驅動的刮板輸送機主傳動系統主要包括：大功率交流永磁電機、連接軸、工作滾筒等部件。可將這些傳動部件歸納為兩種，一種質量大而彈性小，如電動機、滾筒等；另外一種彈性大而質量小，如連接軸等。因此為了更好地分析永磁電機驅動下刮板輸送機主傳動系統的扭振特性，從全局機電耦合角度，將系統等效為一個由若干慣性部件和彈性部件構成的“質量彈性系統”，最終構建了永磁電機-刮板輸送機機頭滾筒的物理模型，如圖1所示。圖1中，J1，J2分別為永磁電機輸出軸轉動慣量與刮板輸送機機頭滾筒轉動慣量；K，C分別為連接軸扭轉剛度與阻尼系數；θ1，θ2分別為永磁電機轉角及刮板輸送機機頭滾筒轉角；ia，ib，ic分別為永磁電機三相定子電流；ua，ub，uc分別為永磁電機三相定子輸入電壓；永磁電機電磁轉矩為Tm；刮板輸送機機頭滾筒負載轉矩為Tl。建模過程中做如下假設： ①磁飽和及永磁體損耗忽略不計，各相繞組的自感和互感都是線性的；②永磁電機轉子無偏心，氣隙均勻；③忽略溫度和頻率變化對電動機參數的影響。

圖1 永磁電機-刮板輸送機機頭滾筒運動物理模型

(1) 首先確定永磁電機驅動的刮板輸送機主傳動系統廣義坐標共5個，如表1所示。其中電磁系統包括3個分別為永磁電機三相定子電量，機械系統包括2個分別為永磁電機轉角與刮板輸送機機頭滾筒轉角。

表1永磁電機驅動的刮板輸送機主傳動系統廣義坐標

Tab.1Generalizedcoordinatesofthemaindrivesystemofthescraperconveyordrivenbypermanentmagnetmotor

廣義坐標電磁系統定子轉子j=1j=2j=3-機械系統電機轉角滾筒轉角j=4j=5qjeaebecΨfθ1θ2q·jiaibic---θ·1θ·2Qjuaubuc---F11F22

(2) 系統廣義動能包括機械系統運動動能和電磁系統磁場能。其中，永磁電機驅動的刮板輸送機主傳動機械系統的動能主要包括：電機軸轉動動能、滾筒轉動動能，可表示為

(1)

永磁電機的磁場能主要包括定子電流產生的磁能以及永磁體轉子產生的磁鏈與定子電流作用產生的磁能，可表示為

(2)

式中：La，Lb，Lc分別為永磁電機三相定子繞組自感系數；H為永磁電機三相定子繞組互感系數。

(3) 系統勢能為連接軸扭轉變形所致的彈性勢能，取彈性力形式為：Fk=K(θ1-θ2)，則系統勢能可表示為

(3)

(4) 系統耗散函數包括電磁系統和機械系統兩部分，可表示為

(4)

式中：Ra，Rb，Rc分別為永磁電機三相定子繞組電阻。

(5)

將式(1)～式(5)代入拉格朗日-麥克斯韋方程

(6)

式中：Ll為拉格朗日算子，可表示為

Ll=Emech+Wm-U

(7)

對于定子繞組A(j=1)，取q1=ea，將式(7)代入式(6)可得定子繞組A的電壓方程為

(8)

同理，對于定子繞組B(j=2)和定子繞組C(j=3)，電壓方程可分別表示為

(9)

(10)

對于機械系統，當取廣義坐標為電機轉角(j=4)，即q4=θ1，式(7)代入式(6)可得永磁電機轉角的運動方程為

(11)

同理可得刮板機機頭滾筒轉角的運動方程為

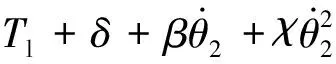
(12)

聯立式(8)～式(12)，可得永磁電機驅動的刮板輸送機主傳動系統機電耦合扭振動力學模型為

Rbib=ub

Rcic=uc

(13)

(14)

式中：ud，Id分別為永磁電機定子直軸電壓與電流；uq，Iq分別為永磁電機定子交軸電壓與電流。

2 平衡點的穩定性及Hopf分岔存在性分析

刮板輸送機在作業過程中，由于運輸煤物料質量的不均勻性會導致滾筒與拖鏈間摩阻力矩的變化，繼而導致系統發生Hopf分岔，并伴隨有失穩振蕩。因此選取摩擦因數β為分岔參數。用[x1x2x3x4x5]T代替[IdIq?ω1ω2]T，式(14)可化為

(15)

式中：A(x,β)為原系統的Jacobian矩陣，f(x,β)為原系統的非線性項。

式(15)的平衡點通過適當的坐標變換可以轉移到坐標原點，因此研究系統平衡點在原點處的動力學特性具有普遍意義，選擇合適的參數得式(15)在原點處Jacobian矩陣和非線性項為

(16)

式(16)特征方程可表示

κ5+λ1κ4+λ2κ3+λ3κ2+λ4κ1+λ5=0

(18)

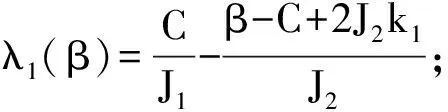
由A(0,β) 特征根的實部可判定式(15)在原點處的穩定性，如果A(0,β)特征根有正實部，則系統在原點處不穩定，將出現失穩振蕩；若A(0,β)特征根的實部全部為負，則系統在原點處漸進穩定；當A(0,β)特征根有零實部時，此時需要考慮系統非線性項f(x,β)的影響。傳統的方法是根據原系統相關參數計算其Jacobian矩陣A(0,β)的所有特征根，進而判斷參數變化時A(0,β)是否有特征根穿越虛軸，該方法計算量大，且很難寫出系統特征根跟分岔參數β的解析表達式。故本文利用Hurwitz判據判定原系統Hopf分岔的存在。原系統在原點Jacobian矩陣的特征方程其系數λi可構成如下Hurwitz行列式

(19)

式中：如果i>5，則λi=0。系數Λi(i=1～5)由分岔參數β確定。基于Hurwitz判據判定原系統Hopf分岔存在性及計算相應分岔參數值的具體流程，如圖2所示。

圖2 永磁電機驅動的刮板輸送機主傳動系統扭振Hopf分岔存在性判定流程

3 系統模型降維及分岔類型判定

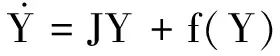
(20)

式中：J為永磁電機驅動的刮板輸送機主傳動系統線性化矩陣的Jordan標準型，f(Y)為非線性部分。將相關參數代入，可得f(Y)的表達式為

f(Y)=inv(T)f(TY,β)=

根據f(Y)表達式，可以看出原系統標準型方程非線性部分不僅與中心流形參量y1，y2有關，而且與穩定流形參量y3，y4有關。因此為了實現對原系統的降維，根據中心流形定理可設

(21)

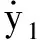
c11=-0.081 64χ，c12=-0.002 097χ，

c15=-0.050 25χ，

c21=-0.220 63χ，c22=0.002 550χ，c25=-0.200 47χ

31.373y2+F1(y1,y2)+U1(y1,y2)

-31.487 8y1+F2(y1,y2)+V1(y1,y2)

(22)

式中：U1(y1,y2)與V1(y1,y2)為含y1，y2的高階項。

25.264y3+F1(y2,y3)+U2(y2,y3)

-25.264y2+F2(y2,y3)+V2(y2,y3)

(23)

式中：U2(y2,y3)與V2(y2,y3)為含y2，y3的高階項。

根據局部不變流形與中心流形定理知，式(22)，式(23)與式(14)的非線性特性相同，在平衡點處具有相同的穩定性及分岔類型。根據規范型理論，可得原系統二階中心流形Hopf分岔穩定性指標為

(24)

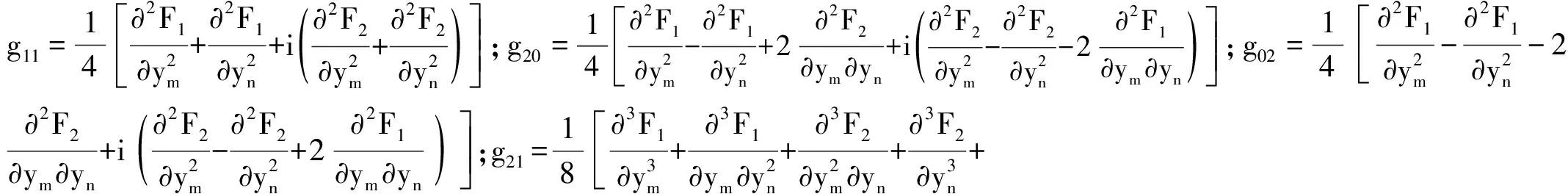
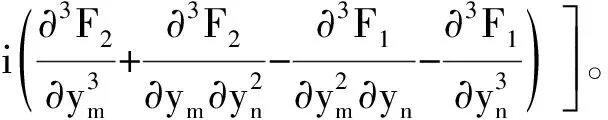
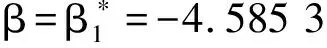
a=0.095 268χ2>0

(25)

a=-0.025 918χ2<0

(26)

由式(25)、式(26)知，當一次線性摩阻系數β=-4.585 3，永磁電機驅動的刮板輸送機主傳動系統在平衡點(0,0)發生亞臨界Hopf分岔，當一次線性摩阻系數β=-15.229 4，永磁電機驅動的刮板輸送機主傳動系統在平衡點(0,0)發生超臨界Hopf分岔，并且系統在臨界點發生的Hopf分岔類型與系統所受平方項摩阻系數(χ)無關。

4 數值仿真驗證

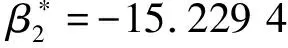
圖3 超臨界Hopf分岔時電機轉速-機頭滾筒轉速相圖(β=-13)

(a) 穩定極限環時間歷程(b) 穩定極限環相軌跡

圖4 超臨界Hopf分岔時電機轉速-機頭滾筒轉速曲線(β=-16，初值為[0.5,0.5,0.5,0.5,0.5])

Fig.4 Response curve of motor speed and drum speed in supercritical Hopf bifurcation (β=-16, initial condition is [0.5,0.5,0.5,0.5,0.5])

(a) 穩定極限環時間歷程(b) 穩定極限環相軌跡

圖5 超臨界Hopf分岔時電機轉速-機頭滾筒轉速曲線(β=-16，初值為[1,1,1,1,1])

Fig.5 Response curve of motor speed and drum speed in supercritical Hopf bifurcation (β=-16, initial condition is [1,1,1,1,1])

圖6 亞臨界Hopf分岔時電機轉速-機頭滾筒轉速相圖(β=-7)

Fig.6 Phase diagram of motor speed and drum speed in subcritical Hopf bifurcation (β=-7)

(a) 穩定極限環時間歷程

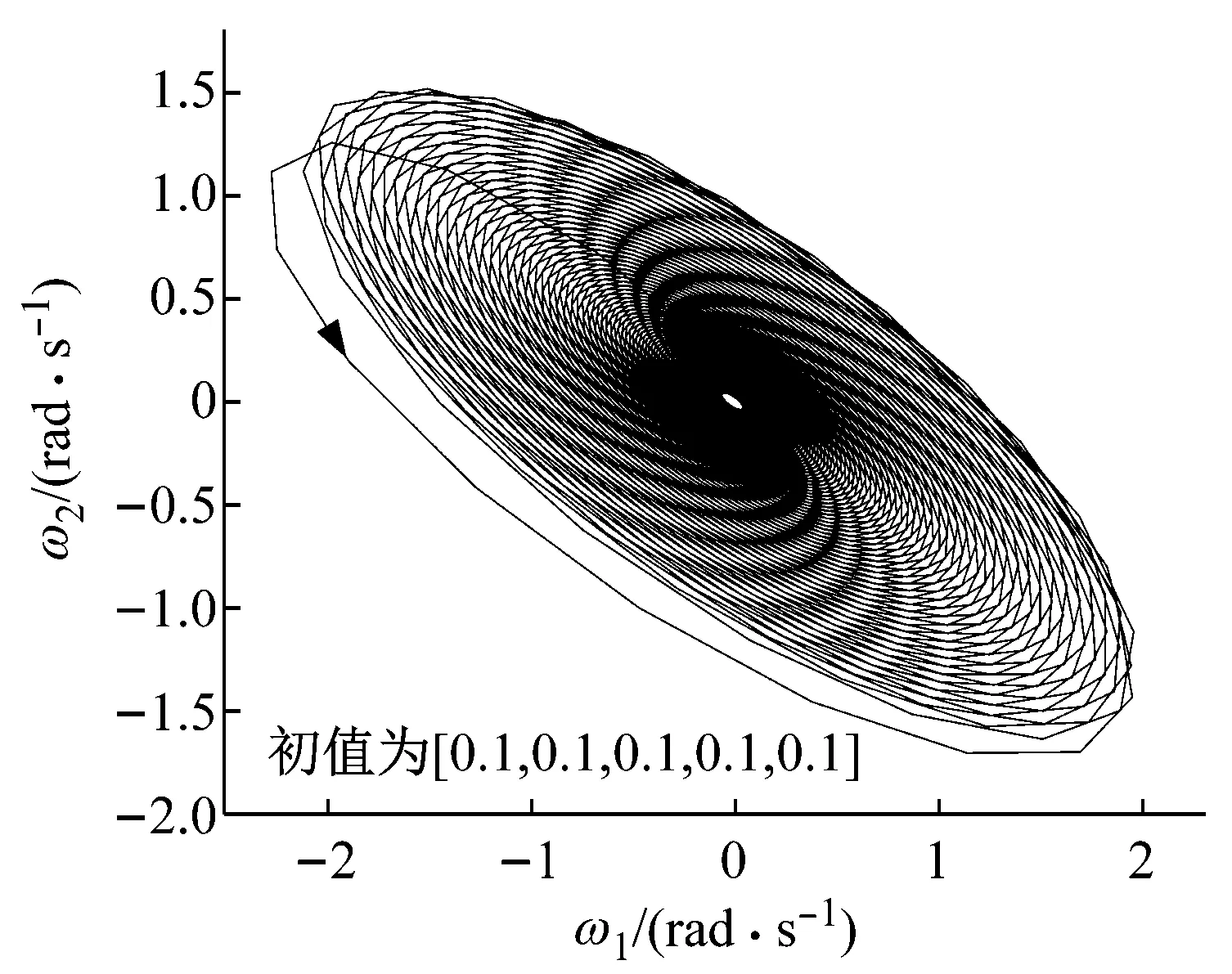
(b) 穩定極限環相軌跡

(c) 不穩定極限環時間歷程

(d) 不穩定極限環相軌跡

綜合文中分析結果可知，永磁電機驅動的刮板輸>送機主傳動軸系Hopf分岔臨界點位置由系統線性部分決定，因此，后期進行大功率永磁電機控制器設計時，可結合文中方法對控制器線性增益部分進行設計，擴大系統的穩定范圍并將系統具有潛在威脅的亞臨界Hopf分岔控制為超臨界Hopf分岔，保證刮板輸送機系統的穩定運行。

5 結 論

本文考慮大功率永磁電機直接驅動形式下刮板輸送機作業過程中運輸煤物料質量的不均勻性，建立了一類非線性摩阻作用下刮板輸送機主傳動系統的機電耦合非線性扭振動力學模型，利用中心流形理論與規范型理論對刮板機主傳動系統扭振Hopf分岔行為進行解析分析。理論分析與數值仿真計算結果表明：

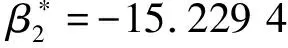
(3) 將大功率永磁電機應用到刮板輸送機上，應該考慮運輸煤物料質量不均勻性的影響，具體應用時應避免在系統亞臨界Hopf分岔臨界點附近工作，根據本文的分析結果，可為后期刮板輸送機主傳動系統亞臨界Hopf分岔的控制研究提供參考。