權數可靠性的假設檢驗探討
謝忠秋
(江蘇理工學院 商學院,江蘇 常州 213001)
1 問題的提出
根據研究,賦權方法已多達20多種。受此影響,即使是運用同一數據、同一無量綱化方法以及同一綜合評價方法,而由于各人選擇賦權方法的不同,也會致使綜合評價的結論大相徑庭。因此,如何對眾多賦權方法所得權數的可靠性進行科學界定,就顯得十分必要。
從現有文獻看,關于權數的研究主要集中在以下幾方面:(1)賦權方法的研究。這也是目前權數研究的主要內容。有主觀賦權法、客觀賦權法、組合賦權法等多達20多種賦權方法。(2)權數的性質研究。在權數具有重要性、模糊性、主觀性、時序性的基礎上,提出了空間性、時空性和函數性等權數新的性質,進一步深化了對權數的理論思考。(3)權數的調整研究。包括對抽樣調查分析中初始權數的調整以及依據方差控制要求的權數調。(4)對權數影響的研究。如無量綱化對屬性權重的影響,之間存在一種傳導機制等。顯然,上述研究進一步豐富和發展了權數的理論和實踐體系。然而,在上述研究中,忽略了權數研究的一個根本性問題,即權數的可靠性研究。事實是,只有當權數可靠了(同樣,在無量綱化和綜合評價方法方面也存在著可靠性的問題),才能帶來綜合評價結果的正確性。相反,容易致使人們對其產生“懷疑”,進而對綜合評價結果也極易產生一種“不信服”感,從而嚴重影響著綜合評價的聲譽。所以,在賦權方法的選擇上,應以所得權數是否具有可靠性為標準。可靠,則該賦權方法可用,所得權數可用。否則,則俱不可用。顯然,在權數研究中,應補上權數可靠性研究這一重要內容。但迄今為止,有關權數可靠性研究的文獻還沒有。也正基于此,本文提出這一問題,并給予實例分析,以期彌補權數研究現有的不足。
2 權數可靠性檢驗的統計量
所謂權數可靠性,從統計學的角度來說,就是指能以多大的概率保證依據某一賦權方法所得出的權數與評價者期望的權數相一致。顯然,概率越大,則意味著依據某一賦權方法所得出權數的可靠性越好。在統計上,解決此問題的路徑是進行權數可靠性的假設檢驗。
為便于理解,本文建立原假設H0:采用某一賦權法所得權數與總體權數沒有顯著差異(沒有差異,則意味著所得權數是具有可靠性),則有:備擇假設H1:采用某一賦權法所得權數與總體權數有顯著差異(有差異,則意味著所得權數不具有可靠性)。而做好權數可靠性假設檢驗的核心是確定檢驗所用的統計量。
考慮到權數具有計數的性質,而卡方檢驗又是一種用途很廣的計數資料的假設檢驗方法。所以,可以運用χ2檢驗,統計量如下:
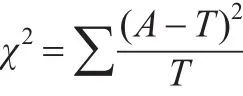
式中,A:實際數,T:理論數,V:自由度,為(行數-1)×(列數-1)
總體權數是客觀存在的,相當于公式中的實際數,而運用某一賦權方法所得出的權數則相當于公式中的理論數。如果說,χ2檢驗的根本思想在于比較理論頻數和實際頻數的吻合程度問題,那么,權數的χ2檢驗的根本思想就在于比較運用某一賦權法所得權數和客觀存在的總體權數的吻合程度問題。顯然,如果總體權數已知,則可以直接運用檢驗。但事實畢竟是,總體權數事先是未知的,這就使得直接運用進行檢驗無法實現。那么,能否通過一定的變換,找到的替換變量,從而完成權數可靠性的假設檢驗呢?經過推導,證明這一想法是可行的。
χ2=的替換變量的尋找過程如下:
設:maxT-T=λi(maxT-minT)
λi是指樣本的最大權數與某一權數的離差占總離差(極差)的比例。
于是有:
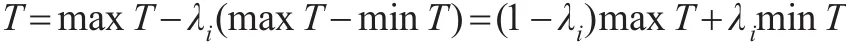
進一步有:
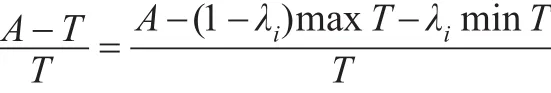
分子兩邊平方:
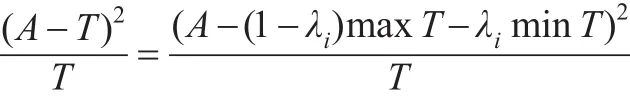
由于:
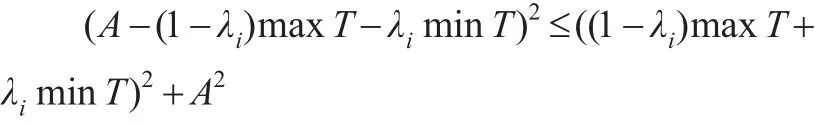
而:
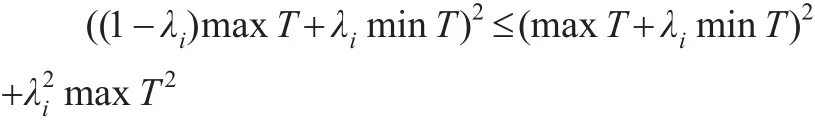
所以:
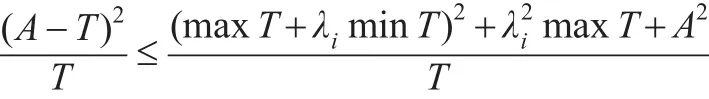
從而也有:
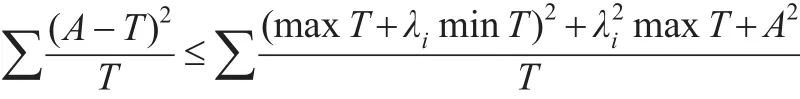
在非負數的情況下,又有:

由權數的性質可知,∑A=1,所以有:
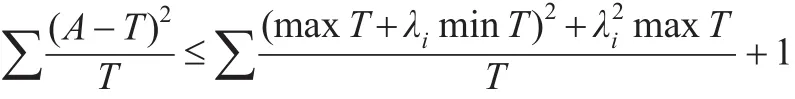
取最大值,則有:
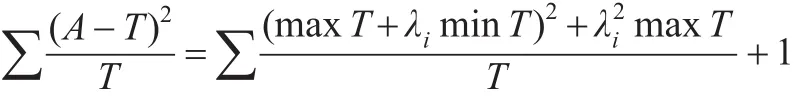
最終有:
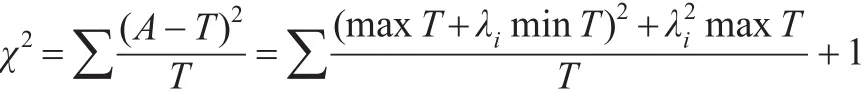
所以,對權數可靠性進行假設檢驗,其步驟如下:
(1)建立原假設H0:采用某一賦權法所得權數與總體權數沒有顯著差異。
備擇假設H1:采用某一賦權法所得權數與總體權數有顯著差異。
(2)計算χ2統計量:
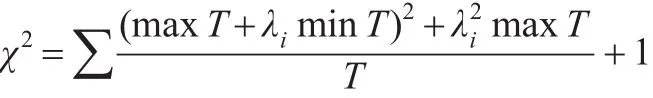
自由度v=(行數-1)×(列數-1)
(3)給定顯著性水平(t(),查卡方界值表,找到(v)。
(4)比較χ2統計量與臨界值χα2(v),當χ2≤χα2(v),則接受H0,拒絕H1,認為采用某一賦權法所得權數與總體權數沒有顯著差異;當χ2≥(v),則拒絕H0,接受H1,可以認為采用某一賦權法所得權數與總體權數有顯著差異。
3 例證運用
例1和例2分別說明了權數可靠性檢驗接受原假設H0和接受備擇假設H1的情況。結果表明,本文所提出的權數可靠性檢驗具有一般性。
例1:有6項指標,分別為A、B、C、D、E、F,采用某種賦權法所求得的權數分別為:0.2、0.15、0.16、0.18、0.11、0.2。那么,依據某種賦權法所得出的權數與總體權數之間是否有顯著差異?計算過程見表1所示。
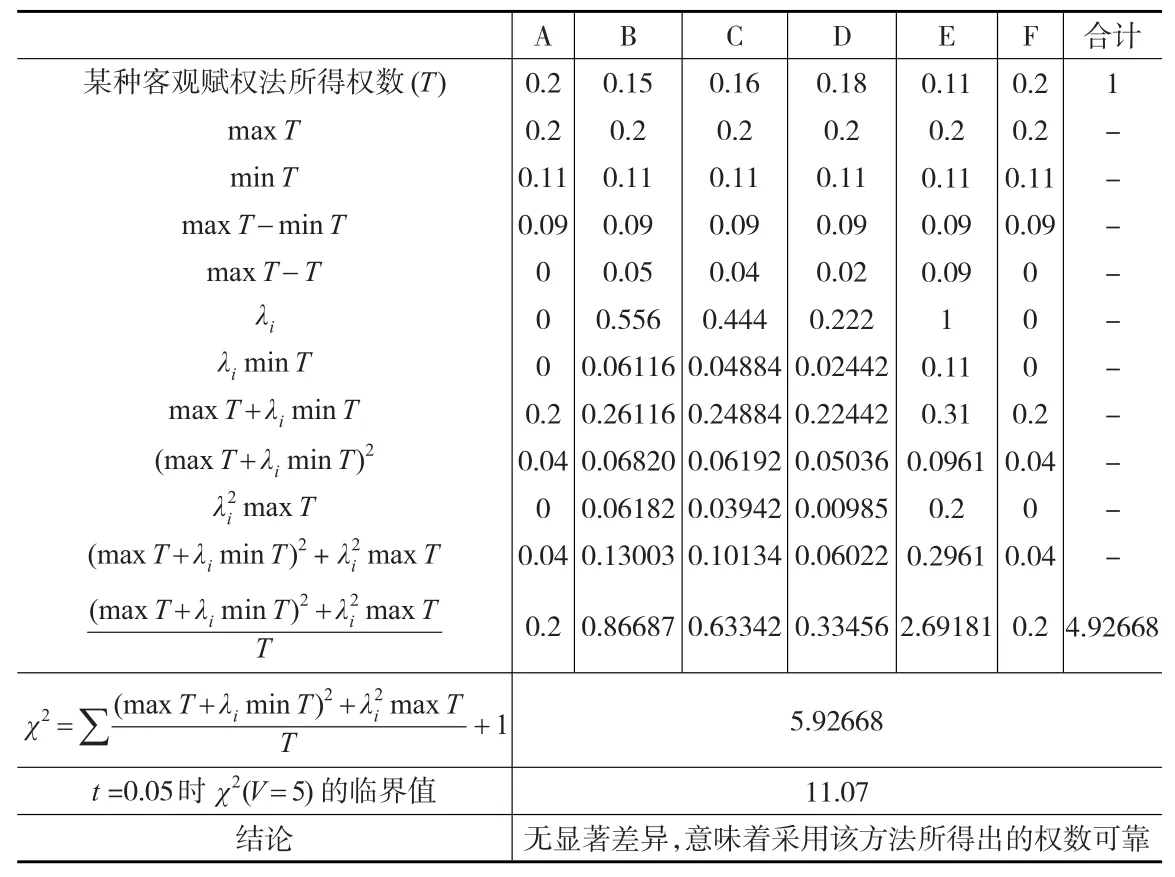
表1權數假設檢驗計算過程
例2:有6項指標分別為A、B、C、D、E、F,采用某種賦權法所求得的權數分別為:0.16、0.13、0.11、0.14、0.18、0.28。那么,依據某種賦權法所得出的權數與總體權數之間是否有顯著差異?計算過程見下頁表2。
需要指出的是,在實際運用時,要注意兩個細節,一是權數的表現形式,不能采用∑T=100這樣的形式,而只能采用∑T=1這樣的形式,之所以如此,根本原因在于保持權數的和等于1這一性質不至于改變。二是在考慮列數或行數時,應將未知的總體權數的列數或行數考慮進去,否則會導致自由度是0而無法取得臨界值。
4 結束語
本文通過運用上述方法對某種賦權法所得權數的可靠性進行檢驗,從根本上解決綜合評價中權數確定無假設檢

表2 權數可靠性檢驗計算過程
驗的現象,以增強賦權法所得權數乃至綜合評價的可信性。

