基于全人口死亡率數據的隨機死亡率模型擬合效果比較

樊 毅，張 寧

（1.中南林業科技大學 經濟學院，長沙 410004；2.湖南大學 金融與統計學院，長沙 410006）

0 引言

近些年來，死亡率的持續下降帶來的平均預期壽命的提高成為了世界各國人口發展的重要特征，我國也不例外。根據國家統計局發布的數據，我國人口的人均預期壽命已經從建國初期的40歲左右增加到了2015年的76.34歲。人的預期壽命的不確定性也會因人們在生活方式上的變化、醫療技術上的創新等因素而增加。預期壽命變動的隨機性不利于養老金成本的核算，并在很大程度上影響到各種養老金計劃的可持續發展，從而很可能會對壽險公司和養老金機構造成損失。綜上所述，在與歷史數據進行比較的基礎上，選擇與我國人口死亡率分布狀況擬合效果較好的隨機死亡率模型，可以使得死亡率預測的精準性得以大大改善，這為我國壽險企業和養老金機構的實踐提供了理論支持。

近二十年來，國內外學者對隨機死亡率模型進行了一系列的研究。其中隨機死亡率模型同時考慮了年齡因素和時間因素對死亡率的影響，使得其預測值更接近實際。目前為止，由Lee和Carter(1992)[1]提出的Lee-Carter（LC）系模型和由Cairns等(2006)[2]提出的CBD系模型是較為經典且運用廣泛的模型。

國內學者雖然有利用死亡率模型對中國人口死亡率進行預測，但是將不同死亡率模型對中國人口的擬合效果進行比較分析的研究相對較少。王曉軍和蔡正高（2008）[3]在全面綜述了各類死亡率模型的基礎上，為中國的死亡率模型選擇提供了合理建議。王曉軍和黃順林（2011）[4]比較分析了幾個較為常用的隨機死亡率模型對我國男性人口死亡率歷史數據的擬合效果，發現在CBD模型基礎上拓展而來的一個模型對中國男性人口死亡率經驗數據的擬合效果最好。段白鴿和石磊(2015)[5]在動態死亡率模型的構建中考慮了超高齡人口死亡率的因素，建立了超高齡人口動態死亡率分層模型，分析了我國人口死亡率的變化狀況和該模型預測的效果。張志強和楊帆（2017）[6]首次在人口死亡率預測中運用了多變點檢測方法，其將Lee-Carter模型與在主成分分析基礎上建立的死亡率模型對多個國家數據進行擬合，發現采用多變點檢測的基于主成分分析的死亡率模型對人口死亡率預測的精確度和穩定性更優。

本文在全面綜述各類死亡率模型的基礎上，選擇了8個運用較為廣泛的隨機死亡率模型，以此對中國1994—2013年總人口死亡率的經驗數據（0～89歲）進行比較分析，并在綜合考慮擬合效果的基礎上作出評價，以此得出最優模型。

1 隨機死亡率模型

死亡率模型主要劃分為確定型和隨機型兩種。其中確定型死亡率模型不考慮時間因素和死亡率未來趨勢對其造成的影響，只假設死亡率與年齡相關，且該種模型的參數由死亡率的經驗數據確定。目前，隨機死亡率模型可劃分為LC系和CBD系死亡率模型。

1.1 Lee-Carter模型

在有關隨機死亡率的研究中，比較著名的是由Lee和Carter于1992年提出的Lee-Carter模型：

其中，αx，βx指年齡因素，kt指隨機時間因素。m(x，t)指在t時刻年齡為x歲的人的中心死亡率，αx指不同年齡段死亡率對數變動的基數；βx指不同年齡段死亡率對數變動的趨勢。kx指時間因素變量，可當作一個隨機游走過程或一個ARIMA過程，表示在t時刻死亡率的變動情況。

如今進行參數估計的方法有許多。Lee和Carter（1992）[1]提出的SVD法 (Singular Value Decomposition)是最早進行參數估計的方法。之后，統計方法更加標準化，注重對全部數據的擬合程度[7,8]。但 Lee和 Miller（2001）[9]認為，應更加注重對數據集最后一年的擬合，因為最后一年的數據對未來死亡率預測的影響要大于其他年份數據。

1.2 包含出生年效應的Lee-Carter模型

2006年，Renshaw和Haberman[10]第一次將出生年效應納入人口死亡率模型：

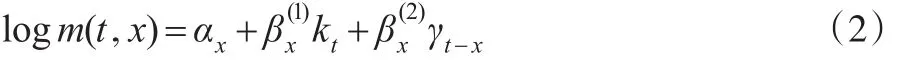
其中，kt指隨機時間因素，γt-x指隨機的出生年效應，是（近似）出生年份(t-x)的函數。Renshaw和Haberman（2006）[10]將英格蘭和威爾士的數據進行分析后，發現相較之前的Lee-Carter模型，加入出生年效應會使人口死亡率模型更加完善，但該模型（RH模型）的穩定性不佳。CMI(2006)[11]發現模型的參數估計值會隨著死亡率數據的年齡范圍變化而變化；Cairns等(2008)[12]用不同時間范圍去擬合模型的過程中也意識到了這個缺陷，他們還進一步意識到用該模型擬合的出生年效應大致存在一個確定的線性趨勢或二次趨勢，這或許會對模型的擬合效果造成影響。

Haberman和Renshaw（2011）[13]令RH模型中的=1以解決其穩定性問題，具體簡化形式如下：

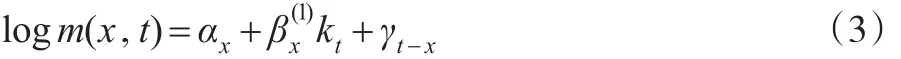
Currie等(2006)[14]在簡化了RH模型后，建立了APC模型：

該模型能夠很好地擬合美國的歷史數據，也能解決RH模型在上文中提到的穩定性問題[11]。

1.3 CBD模型及它的拓展模型

針對高齡人群，Cairns等(2006)[2]提出了一個基于Logistic轉換的CBD模型：

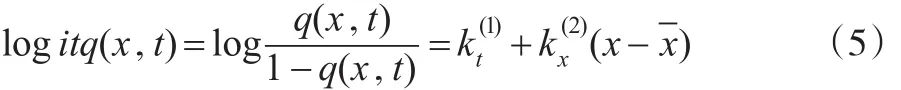
其中，q(x，t)=1-exp(-m(x，t))，指在t年內x歲的人死亡的概率，-x為樣本年齡均值，為具有漂移項的雙變量隨機游走kt=kt-1+μ+cZt，因此該模型也被稱為雙因素死亡率模型。此外，他們在分析中還詳細說明了如何利用貝葉斯方法在模擬中包含參數的不確定性。

之后，Cairns等(2007)[15]進一步拓展了CBD雙因素模型：

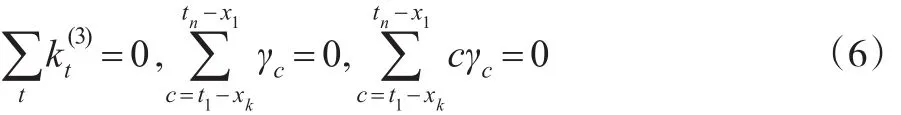
Cairns等(2008)[12]將原始模型進一步簡化，建立了兩個模型，一個模型是令=0，見公式（7）；另一個模型是令是零，用更復雜的年齡-出生年效應因子替換，見公式（8）：

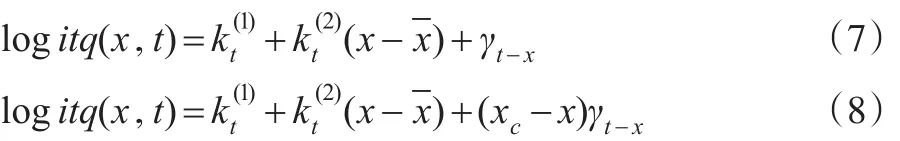
1.4 Plat模型

Plat(2009)[16]在審查和分析LC系和CBD系等死亡率模型后，建立了四因素死亡率預測模型：

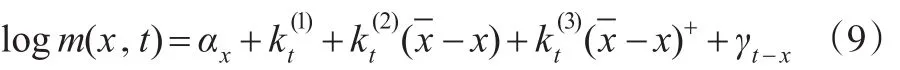
其中，αx與Lee-Carter模型中的類似；代表各年齡死亡率隨時間的變化程度；指各年齡段的人死亡率改善水平的差別；是指由于濫用藥物、暴力或酗酒等原因而使低齡人群的死亡率出現波動，此處用(-x)+=max(-x，0)來代替-x)，目的是使死亡率-年齡曲線變動趨勢與以往數據相吻合。若僅僅預測高年齡組人群死亡率，可剔除，使模型更加簡化：

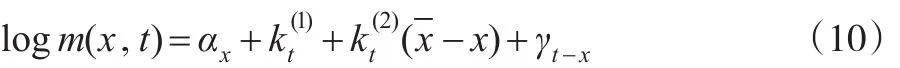
γt-x指出生年效應，與前文模型所指意義類似。

2 隨機死亡率模型擬合效果的比較分析

2.1 隨機死亡率模型的選擇

下頁表1將前文提到的隨機死亡率模型進行了匯總。其中，LC模型是出現最早的隨機死亡率模型且該模型不包含出生年效應；RH模型和APC模型把LC模型進一步拓展，但APC模型比RH模型更穩定。CBD模型是針對高齡人群、基于Logistic轉換的雙因素模型；將M7模型進一步簡化，可得到M6模型和M8模型；因納入二次年齡效應和出生年效應兩個成分，使得M7模型穩定性更強；M8模型同為CBD系拓展模型，它包含了年齡-出生年效應因子；Plat模型即四因素死亡率預測模型。

2.2 模型參數的估計方法

本文在進行參數估計時，假設死亡人數D(x，t)近似服從Poisson，即：

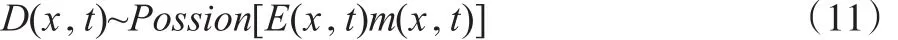
其中，D(x,t)指在t年時x歲的人的死亡數量，用E(x,t)指在t年時x歲的人平均死亡風險暴露人數，m(x，t)與之前模型類似。為了避免空缺數據單位對參數估計的影響，本文將提前擬定權數而準許數據過度離散。Yxt指在t年時年齡為x歲的人的死亡數量。基于Yxt的一階矩和二階矩，可得到關系式如下：

表1 8個隨機死亡率模型

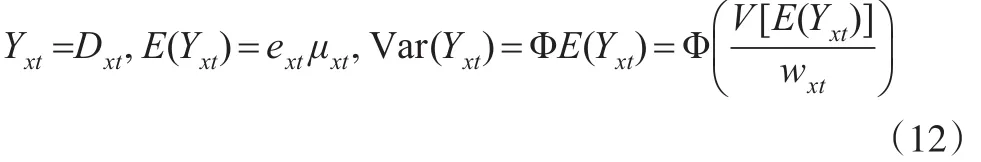
其中，Φ為比例參數，wxt為權重函數，V[E(Yxt)]=E(Yxt)為方差函數。令數據缺失時的權數等于0，反之等于1。為了使模型之間的比較基礎一致，本文將使用死亡率q(x，t)的模型轉換成m(x，t)，如下：m(x，t)=-log[1-q(x，ty)]。這樣能夠對表1中的8個模型都使用m(x，t)來計算模型的極大似然估計值。

對于一個給定的模型，要將符號m(x，t)擴展成m(x，t，θ)來代表參數之間的依賴性，其中θ表示待估計的參數向量，同樣地：

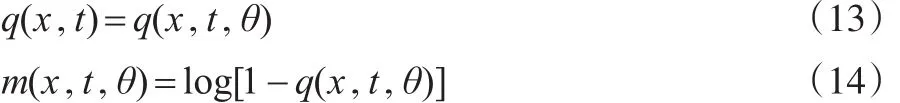
對上述8個模型進行參數估計時，使用的是極大似然估計法，具體形式如下：

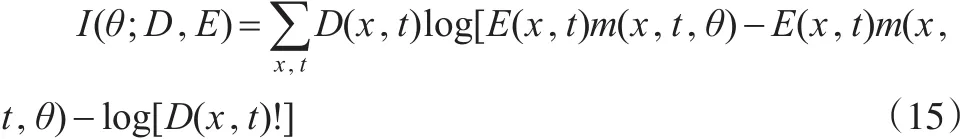
最后，為了得到各參數的估計值，使用牛頓迭代法，其公式如下：

2.3 模型的選擇標準

2.3.1 殘差圖檢驗

本文使用了中國1994—2013年0～89歲的綜合死亡人數和平均死亡風險暴露人數數據，來更好地比較所選取的8個模型的擬合效果。圖2和圖3以殘差圖的形式，在泊松誤差結構假設下，分別反映了年齡、日歷年和出生年對死亡率的影響。通常按照殘差分布來選擇模型。依據圖2和圖3，可看出8個模型都捕捉到了時間效應，但是僅僅只有RH、APC、M6、M7、M8以及Plat模型反映出了出生年效應。此外，從CBD模型殘差圖中能夠得知，其年齡殘差圖以及出生年殘差圖都呈現了波動劇烈的特征，這在一定程度上表明了年齡效應以及出生年效應并沒有在其中得到反映，但是從其時間殘差圖得知，時間效應能夠在該模型中得到有效地反映，因為其時間殘差圖是均勻分布在零軸兩側；LC模型也未能較好地捕捉出生年效益，因其對應的殘差有輕微的波動，但該模型卻很好地捕捉了年齡效應和時間效應；從殘差圖可看出，RH模型和APC模型的擬合程度很高，三個成分的殘差在零軸兩側均勻分布，但是RH模型的擬合效果的穩定性優于APC模型。M7模型的殘差圖分布均勻且最接近零軸，因此該模型的擬合程度較高，優于M6模型和M8模型；與M7模型相比，雖然Plat模型的殘差分布均勻，但在零軸附近的偏移程度較大，因此該模型對數據的擬合存在一定的偏差。

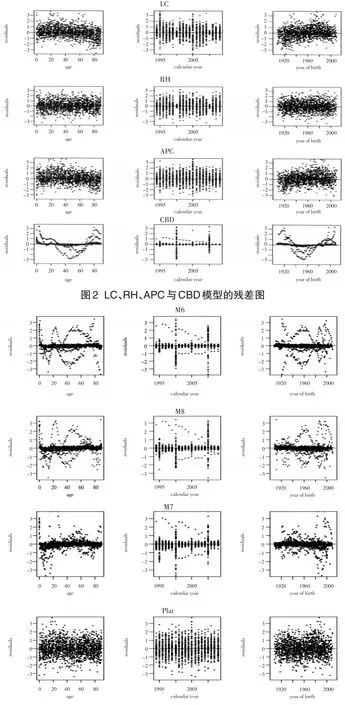
圖3 M6、M8、M7與Plat模型的殘差圖

2.3.2 AIC和BIC比較法

通常，極大似然估計值的大小受模型中參數個數多少的影響，參數個數越多估計值越大，則會使模型過度參數化，可以通過懲罰過度參數化的模型來避免該問題。本文將運用貝葉斯信息準則（BIC）和赤池信息量準則（AIC）來觀察添加的每一個參數對模型的極大似然估計值的影響。就比較標準而言，AIC和BIC考慮到了模型的擬合質量和簡潔度，同時在比較時不必考慮模型之間有無相互嵌套關系，此外，BIC沒有假設先驗模型的排序。通過得出表1中的8個模型的AIC值和BIC值及其大小順序（見表2），能夠發現RH模型對中國的死亡數據的擬合程度最高，其次是Plat模型，再次是APC模型。

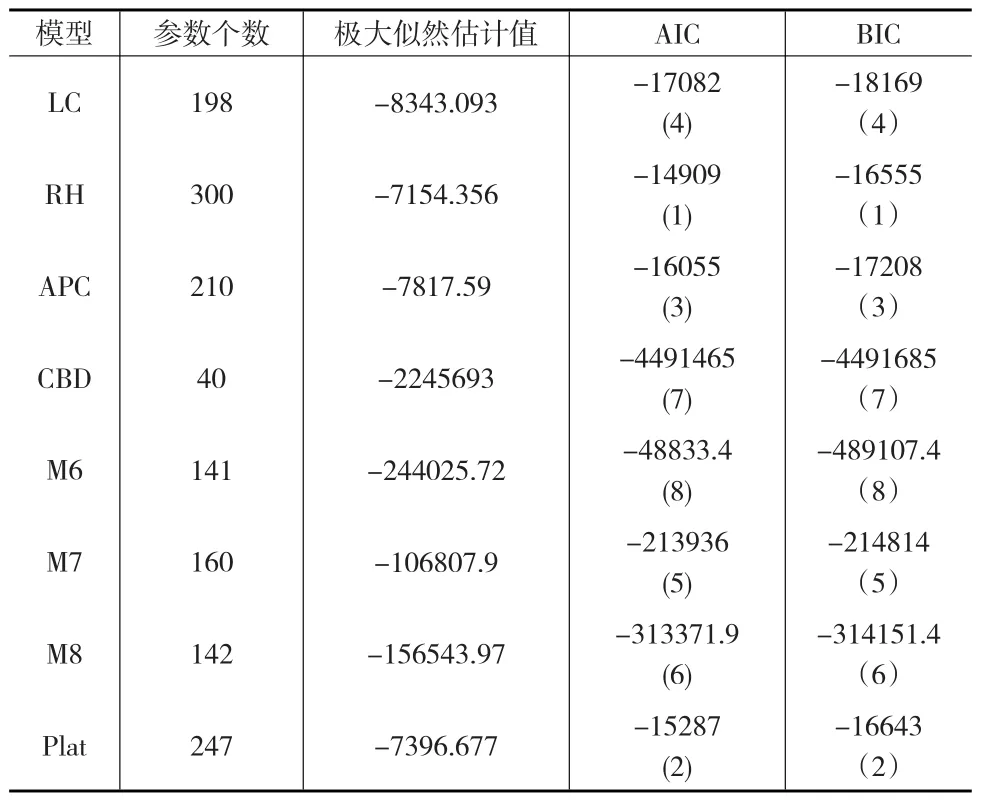
表2 8個隨機死亡率模型的AIC和BIC值及其大小順序（括號中）

2.3.3 嵌套模型的似然比檢驗

嵌套模型是一般模型的特殊形式。例如，在簡化RH模型基礎上提出的APC模型是其嵌套模型。對于嵌套模型，通常采用似然比檢驗的方法，該檢驗的原假設為嵌套模型的擬合效果好，備擇假設為更一般的模型擬合效果更優。就APC和RH模型而言，設APC和RH模型的極大似然估計值分別為和，其參數估計個數分別為v1=214，v2=304。假設原假設成立，極大似然比統計量是2(-l1)，可知它近似服從卡方分布，自由度d.f.為α 為置信水平），那么拒絕原假設，得出RH模型的擬合效果更優的結論。

如表3所示，表2中的嵌套模式的模型總共有6對。通過表3可以明顯發現P值都小于α，因而拒絕原假設，得出一般模型的擬合效果優于嵌套模型的結論。

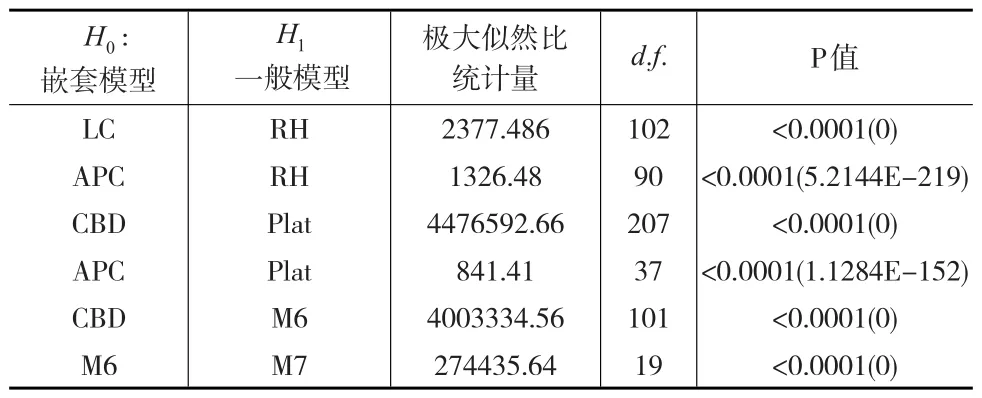
表3 一般模型與嵌套模型的似然比檢驗

2.3.4 參數的穩定性檢驗

本文選取了RH模型、APC模型和Plat模型，上述三模型均為BIC值較大的死亡率模型，并使用極大似然估計法對年齡0～89歲的人進行參數估計，然后分別作出參數分布圖，如圖4所示。本文選取了1994—2013年和1997—2013年的中國綜合死亡人口數據和綜合平均死亡風險暴露數據來對上述三個模型進行參數估計。1994—2013年以及1997—2013年的數據擬合的模型中每一項的分布見圖3，其中，散點使用的是1994—2013年的數據，折線使用的數據為1997—2013年。令年齡在[0,89]內取值,日歷年分別在[1994,2013]和[1997,2013]內取值。

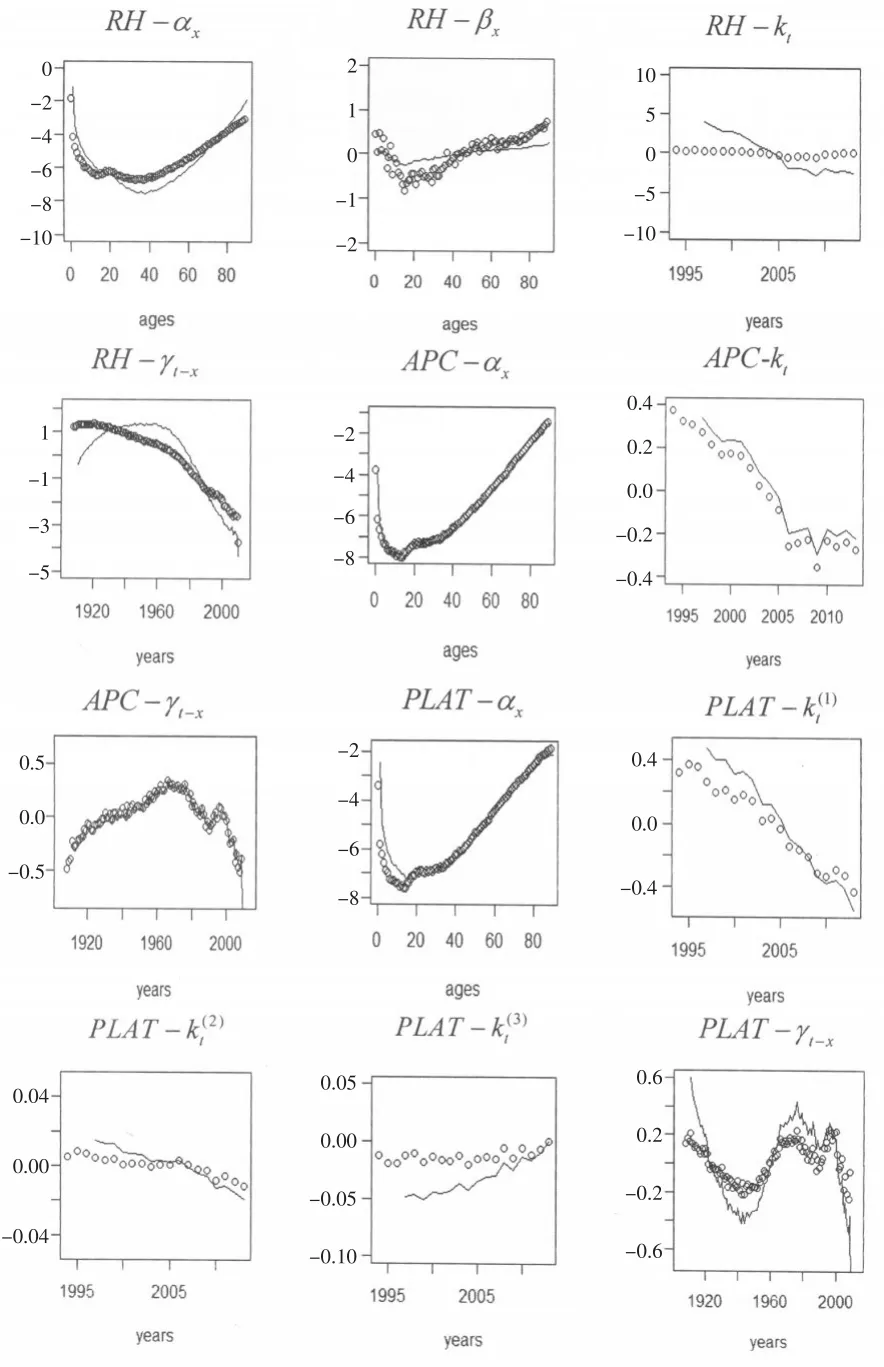
圖4 RH、APC、Plat模型的擬合穩定性檢驗圖

從上述三個模型的檢驗圖中看到它們出生年效應顯著，其出生年效應曲線在t-x≥1970時均呈現出下降趨勢。

參數是否具有穩定性是衡量模型優劣的重要指標。若模型的穩定性較好，則該模型在使用不同時間段數據的情況下，得到的兩組估計值曲線相吻合。對于APC、RH和Plat模型，它們的參數估計圖在年齡項的擬合上較為接近，且相對穩定，即使在擬合模型參數時使用的時間段較短，其參數圖也改變不大。RH模型對于出生年效應的擬合效果相對較差：1997—2013年數據擬合的出生年指數圖是先上升后下降的，而1994—2013年數據擬合的指數圖卻有下降趨勢。不同于RH模型，APC模型和Plat模型在時間段較短的情況下，其預測趨勢與原圖線大致吻合，故其擬合效果較優，但出生年指數因數據變少，方差變大而擴大了其取值范圍。Plat模型出生年指數范圍由原來的(-0.2,0.2)擴大至(-0.6,0.6)。

3 結論與建議

本文對所選取的8個隨機死亡率預測模型的擬合效果進行比較與分析。發現當以殘差圖的形式，在泊松誤差結構假設下，每個模型都捕捉到了時間效應，且除了LC模型和CBD模型外都捕捉到了出生年效應。研究表明RH模型、APC模型和M7模型擬合程度最優，而LC模型和CBD模型擬合程度較弱。就BIC檢驗而言，能夠發現RH模型對中國的死亡數據的擬合程度最優，其次分別是Plat模型和APC模型。就參數穩定性而言，APC模型、RH模型和Plat模型的參數估計圖在年齡項的擬合上較為接近，且相對穩定，預測結果較為準確。因此，在綜合考慮所有的死亡率模型擬合效果后可以得出，APC模型與我國的人口死亡狀況最相適應。

從以上結果能夠得出，并不存在一個可以有效解決我國人口死亡狀況擬合中存在的各種問題的隨機死亡率模型。這不僅在一定程度上反映出難以獲取人的死亡狀況的發展變化規律；同時也提出了進一步的要求，需要對現有的關于人口死亡率預測的方法及模型進行優化。