基于DCE-WLS法的投入產出表更新比較研究

楊傳明

（1.蘇州科技大學 商學院，江蘇 蘇州 215009；2.蘇州大學 商學院，江蘇 蘇州 215021）

投出產出表是宏觀調控國民經濟、科學制定產業(yè)政策的重要基石。由于投出產出表編制異常復雜困難，需要耗費大量人力、物力與時間，因此中國每五年（逢2及逢7年份）通過全國性普查編制正式投入產出表，期間逢0及逢5年份修正延長表一次。即便如此，每張投入產出表及延長表公布時滯也長達2～4年，無法及時反饋最新內外部環(huán)境變化。因此，采用何種高效率、低成本的方法更新投入產出表，提升非編表年份投入產出分析精準度及穩(wěn)健性，具有十分重要的意義。

1 文獻綜述

總體而言，當前投入產出表更新方法主要包括調查更新和數(shù)學更新兩大類。調查更新主要采用實際調查及專家訪談方法[1,2]，所得數(shù)據(jù)相對真實，但仍面臨著工作量大、運行成本高、主觀性較強等諸多問題。因此，數(shù)學更新逐步成為主流研究方法，其利用常規(guī)統(tǒng)計數(shù)據(jù)，通過設計數(shù)學方法，將基準年份投入產出表更新為非編表目標年份的投入產出表。數(shù)學更新方法進一步可分為統(tǒng)計更新法及優(yōu)化更新法兩大類。

1.1 統(tǒng)計更新法

統(tǒng)計更新法根據(jù)更新過程投入產出表相關系數(shù)變化與否，又可以分為系數(shù)恒定法及RAS類方法兩種類型。

（1）系數(shù)恒定法

該方法依據(jù)產業(yè)結構受到技術矩陣直接影響的原理，不更改投入產出矩陣系數(shù)，而利用情景分析法、諾依曼射線等方法預測經濟增長途徑。在此基礎上，學者或直接假定基準年份與目標年份產業(yè)增加值與交易值具有相同比例，依據(jù)基準投入產出表直接預測目標年份的產業(yè)結構[3,4]，或基于基準投入產出表中的產業(yè)比例預測與最終需求一致的目標年份總產出[5]。但由于經濟發(fā)展充滿了不確定性，導致產品生產過程中的中間投入與勞動力及資本比例呈現(xiàn)波動狀態(tài)，造成該類方法在實際操作過程中容易出現(xiàn)較大誤差。

（2）RAS類方法

為了解決系數(shù)恒定法中存在的問題，Hiramatsu等提出了雙比例函數(shù)方法（RAS）[6]。RAS法首先假設投入產出表中間投入受到諸多系數(shù)的綜合影響，如因價格變動而產生的代用系數(shù)、因技術進步而產生的制造系數(shù)等。而后借用基準投入產出表的直接消耗系數(shù)，通過設置代用矩陣R和制造矩陣S操作修正目標投入產出表控制系數(shù)，以彌補數(shù)據(jù)滯后問題。最后采用k次迭代計算代用矩陣和制造矩陣，將各個過程趨于收斂，得到更新后的投入產出表。具體公式如下：

該方法原理清晰、簡單易行，然而Wiebe等學者在利用STPE、MAE等指標進行精度評價后，發(fā)現(xiàn)RAS法整體平均誤差率仍然偏高[7]。究其原因，在于RAS法存在初始矩陣可靠度存疑、無法處理負值、約束條件不夠完善等系列問題，僅能適應目標表行和以及列和均為已知的情況，因此國內外學者對其進行了擴展與改進，提出了MRAS、TRAS、GRAS等拓展性方法。

MRAS法借助統(tǒng)計年鑒及經濟普查，收集部分目標年份投入產出表中特定或聚合單元格數(shù)據(jù)，再運用這些額外數(shù)據(jù)提升更新表的精準性[8]。但由于獲得的數(shù)據(jù)往往面臨著來源不一、細分困難等情況，極易導致約束條件互斥而造成模型無解。為此，Allen等學者進一步提出TRAS法[9]，將At分解為已知確定信息及不確定誤差兩個部分：

該方法計算原理與RAS法一致，只需對目標矩陣的行列進行調整。但主要問題在于要求具有一定規(guī)模，規(guī)模較小則無法實現(xiàn)有效求解。

Deetman等進一步提出了GRAS更新法，通過保持更新后矩陣所有元素符號不變，維持At及Ab對應元素的一致性，以有效應對初始矩陣容易出現(xiàn)負值的情況[10]。該方法雖然在一定程度上解決了RAS法存在的問題，但當面臨較多聚合約束條件時，仍無法有效保障模型求解精度。

1.2 優(yōu)化更新法

該類型方法借助衡量基準值與目標值間的距離整合數(shù)據(jù)，以求更好滿足投入產出矩陣的附加約束要求。根據(jù)距離求解方式不同，優(yōu)化更新法可以分為絕對值類、交叉熵類、最小二乘類三種方法。

（1）絕對值類方法

絕對值法最初是以最小差值形式出現(xiàn)的[11]，公式如下：

考慮到不同系數(shù)對于更新精準度影響不同，特別是大系數(shù)變化對投入產出表更新精度影響大于小系數(shù)，學者對于公式（3）中的系數(shù)變化又賦予了不同的權重[12]，形成了下式：

公式（4）為標準化絕對差值法，通過對小系數(shù)變化加大懲罰，保證了更新焦點集中于大系數(shù)的變化。公式（5）為加權絕對差值法，該方法直接利用基準年份投入產出表系數(shù)作為權重，隱含了大系數(shù)不存在大變動的假設條件。

（2）交叉熵類方法（CE）

Golan等學者將信息理論中的熵概念引入投入產出表更新工作中，借助最小化新值與先驗估計概率間距離的交叉熵指標，構建公式（6）求取最接近基準表的目標表[13]。

Beruvides等學者從保號、方向和接近度檢驗等角度對交叉熵類法考察后，認為該類方法可以高效利用現(xiàn)有信息，較好保持投入產出表系數(shù)矩陣的穩(wěn)健性[14]。但缺點在于對交易流量精度控制度不足，容易導致基準和目標投入產出表存在離差期望小而離差方差大的不均衡狀態(tài)。

（3）最小二乘類方法（LS）

Okuhara等學者基于計量經濟學中的最小二乘法[15]，設計了公式（7）。

該方法基于逐次逼近原理將差值平方和引入目標函數(shù)完成更新工作，可以較為簡便地獲取更新數(shù)據(jù)。但缺點是只能進行非線性優(yōu)化，且不能確保一定可獲得全局最優(yōu)解。為此，部分學者提出了標準化最小二乘法[16]，公式如下：

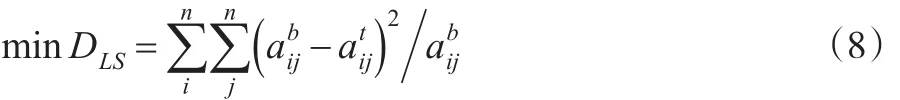
為了保證原有矩陣單元格符號不變，Ding等又通過引入?yún)?shù)≥0，提出了二次最小二乘法（DLS）[17]：

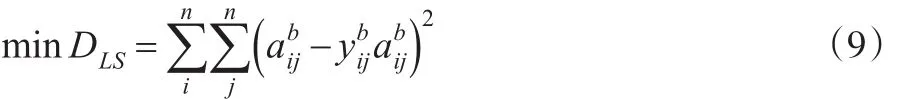
當前最小二乘類方法由于未充分考慮投入產出表中不同矩陣系數(shù)對更新精度的不同影響程度，一定程度上影響了更新表的數(shù)據(jù)質量。

1.3 更新法總結

在所有投入產出表更新方法中，公認最為有效、使用最為廣泛的是RAS類、LS類及CE類方法。究其本質，三類方法存在一定的共性，即均通過設置不同距離最小化基準年份和目標年份投入產出表間的差異，區(qū)別僅在于對接近程度距離的定義不同。LS類方法將最小化基準及目標投入產出表各數(shù)值之差的平方和定義為距離；CE類方法通過最小化基準年份投入產出表的先驗估計概率交叉熵計算距離；RAS類方法則主要通過調整矩陣流量進行更新，本質上可以看作CE類方法的一個特例。在實際運用中，三種方法除了各自存在一定優(yōu)缺點外，仍面臨著一個共性問題，即均主要從技術層面將目標表向基準表機械推近，一定程度上忽略了部分先驗信息，造成無謂損失。

為此，本文在分析主流更新方法原理及優(yōu)缺點的基礎上，綜合考慮聚合約束條件，分別改進CE類及LS類方法，引入信息權重矩陣，組合創(chuàng)立DCE-WLS法，以求提升投入產出表更新的精準度和穩(wěn)健性。

2 DCE-WLS法構建

2.1 DCE法設計

針對CE類方法存在的優(yōu)缺點，本文提出了一個新的雙系數(shù)CE方法（Double Coefficient CE Method,DCE），首先將距離定義為：

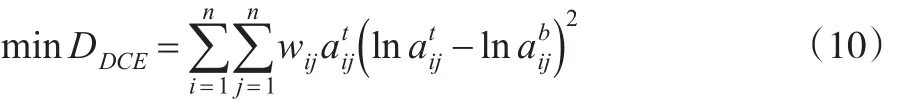
而后利用拉格朗日乘數(shù)法對式（10）進行解析，當exp(-1)≤時：

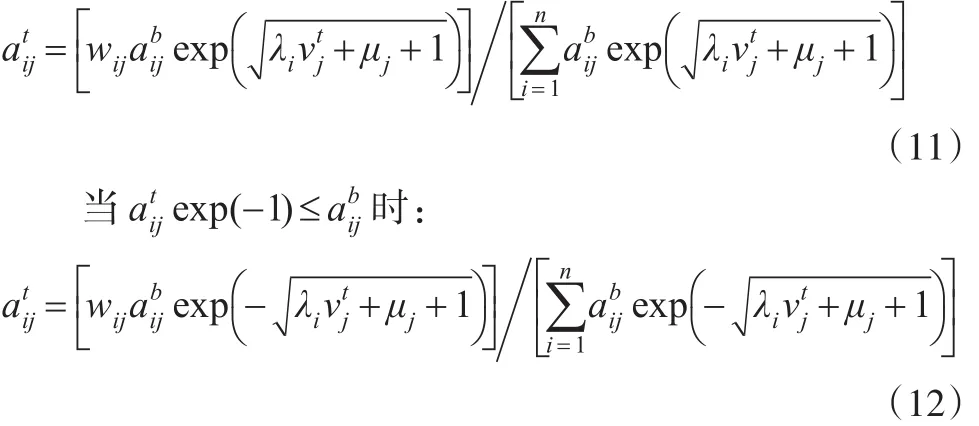
一般而言，經典CE類方法運算主要取決、向量列和和單一拉格朗日乘數(shù)λi三個因素，為了提升更新精準度，DCE法進一步引入了雙拉格朗日乘數(shù)λi和μj，以更好防止各種矩陣系數(shù)的劇烈波動。且DCE法針對基準值和目標值比較存在的兩類情況，設置了不同更新公式，更好地厘清了信息熵使用范圍、夯實了信息熵使用基礎。此外，DCE法通過引入信息權重矩陣Wn×n（wij為其中元素），力圖擺脫機械式的強制均衡，減少有效信息損失度。

2.2 WLS法設計

Kopidou等學者通過實驗分析，認為相較CE類方法而言，LS類方法可以更好地提升交易流量精度，但對系數(shù)矩陣控制度仍較為欠缺[18]。為了更好顧及投入產出表中不同系數(shù)的精度要求，本文將LS類方法拓展為權重LS法（Weight LS Method,WLS），具體定義為：

WLS法依據(jù)系數(shù)變化情況對其賦予不同權重，特別針對大值系數(shù)的變動加大了懲罰力度，從而在確保交易流量精度的同時，更好維持了系數(shù)矩陣的平穩(wěn)性；同時也引入了信息權重矩陣降低先驗信息的損耗。

2.3 信息權重矩陣構造

為了提升投入產出表更新精度及效率，本文針對性地設計了信息權重矩陣。首先結合統(tǒng)計年鑒、行業(yè)報告等資料對基準年份投入產出表進行數(shù)據(jù)甄別。將相關數(shù)據(jù)歸納為三個類型，第一類是確定數(shù)據(jù)，可以直接無修改引入新表；第二類是不確定數(shù)據(jù)，其數(shù)值雖不確定，但已經獲知更新后數(shù)據(jù)的合理取值區(qū)間；第三類則是未知數(shù)據(jù)，數(shù)值與取值空間均不明確。

針對第一類確定數(shù)據(jù)，將其在信息權重矩陣中W對應的取值為正無窮或一個極大的數(shù)值，以保證數(shù)據(jù)更新過程維持不變。對第二類不確定數(shù)據(jù)而言，假設取值空間為合理預測取值區(qū)間長度成反比，區(qū)間長度越小即代表該數(shù)據(jù)越明確。第三類未知數(shù)據(jù)對應的wi3j則直接設置為1，對更新過程不產生任何附加影響。

2.4 約束條件修正

LS類方法和CE類方法的約束條件為：

其中式（14）和式（15）是為了尋求流量加總平衡，式（16）目的是保障算式意義而設置的非負約束。雖然以上約束已經能基本滿足更新工作要求，但從經濟學角度來看，由于存在產業(yè)結構變化、技術水平提升等諸多具有長期過渡性的復雜影響系數(shù)，使得一定時期內投入產出表系數(shù)的演化相對穩(wěn)定而緩慢，直接導致非負約束在實際求解過程中，往往將最優(yōu)解集中趨至非負邊界，造成目標投入產出表中存在大量零值無意義堆積情況。為了更好地應對影響系數(shù)聚合約束條件的繁雜情況，本文設置零值約束公式（17）：

式（17）使得當初始系數(shù)為零時，更新系數(shù)也為零；初始系數(shù)非零時，更新系數(shù)也非零。從而確保目標投入產出表能夠有效繼承基準表的零值結構，更好地保證了目標表質量。

2.5 DCE-WLS法加權設置

由上文分析可見，DCE法與WLS法各具優(yōu)點，DCE法能夠更好地控制目標表系數(shù)矩陣與基準表的相似度，而WLS法則能更好地實現(xiàn)目標表交易流量與基準表的接近精度。在更新工作開始前，若能明確目標表系數(shù)矩陣與基準表相似度較高，則可以直接采用WLS法，若知道目標表交易流量與基準表比較接近，則使用DCE法。但在實際計算中，由于無法確切掌握目標投入產出表的平衡度，使得DCE法及WLS法的適用度難以直接判斷。此外，由于兩種方法計算根基均為距離測算，使得兩者結合成為可能。因此，為了綜合利用兩種方法的優(yōu)點，保證更新結果更為精準，本文將目標更新方法定義為DCE和WLS加權之和，記為DCE-WLS法：

其中ω為權重，可依據(jù)考慮系數(shù)矩陣相似度和交易流量精度的偏重進行設置，為了綜合確保更新的平衡性，本文令ω=0.5。

3 實例比較驗證

評價更新方法優(yōu)劣主要是比較所得目標投入產出表的數(shù)據(jù)質量，第一種比較方式是與調查所得的目標年份真實數(shù)值進行對比，第二種方式是與基準年份數(shù)值進行比較。為了更好分析DCE-WLS法效果，選擇GRAS、STAD（標準化絕對差值法）、TLS（二次最小二乘法）、MCE(標準交叉熵法)作為比較方法，分別運用5種方法完成更新工作，再揀選統(tǒng)計指標進行精準度及均衡性比較。

3.1 統(tǒng)計指標選取

為了更好衡量更新投入產出表與參照表數(shù)值的接近程度，本文揀選了7個具有互補性的統(tǒng)計指標，分析如下：

第一，標準誤差百分比（STPE），作用在于衡量更新數(shù)值標準化的整體精度。式中ait

j為更新所得的直接消耗系數(shù)，aif j為實際直接消耗系數(shù)。

第二，均方根誤差（RMSE），借助此指標可以推算更新數(shù)值的離散程度。

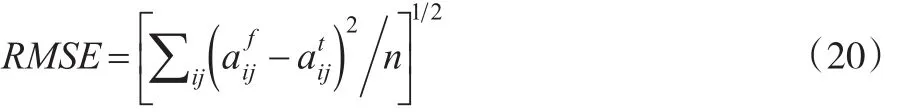
第三，泰爾U值（THeil U），用于衡量流量更新數(shù)據(jù)與最小真實數(shù)據(jù)的誤差。

第四，平均絕對值誤差（MAE），作用在于比較更新數(shù)據(jù)與真實數(shù)據(jù)的平均絕對值誤差。

第五，加權絕對偏差（WAD），該指標通過權重設置分析更新數(shù)據(jù)與真實數(shù)據(jù)偏差。

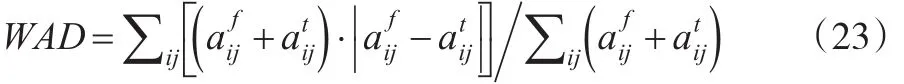
第六，伊薩德/羅曼諾夫相似性指數(shù)（SIM），用于分析相關系數(shù)推算更新數(shù)據(jù)與真實數(shù)據(jù)誤差。

第七，信息損失（INO），該指標以基準數(shù)據(jù)為衡量標準，分析更新表與基準表間的信息損失度，反映計算方法的穩(wěn)健性。

3.2 比較分析

對于投入產出表的5種更新方法，本文采用GAMS軟件24.0版本進行編寫，并以NLPPATH模塊求取各方法的全局最優(yōu)解。

首先采用第一種比較方式分析更新方法的精度。鑒于最新可得的為2015年投入產出表，本文以2012年中國投入產出表為基準表，利用5種方法分別推導，得出更新的2015年投入產出表，再利用統(tǒng)計指標與真實表進行更新精準度對比，得到表1。

表1 更新方法精準度比較

表1統(tǒng)計指標數(shù)值中，前五項統(tǒng)計指標數(shù)值越小越好，SIM值則以接近1為佳；各更新方法的綜合得分為每項統(tǒng)計指標分別排名的平均數(shù)值，數(shù)值越低顯示排名越好、精度越高。由表可見，DCE-WLS法綜合得分最優(yōu)，STPE、RMSE、Theil U、MAE、WAD 五項指標數(shù)值分別 5.8582、0.0159、0.1303、0.0310、3021.5，為 5種更新方法均值的87.15%、91.91%、94.42%、84.24%和93.87%，且均為最低值；SIM值則在5種方法中離標準值1最近，達到了0.758，為均值0.699的108.44%。由此可見，DCE-WLS法的更新結果最為精準。

鑒于在實際操作過程中，往往無法獲得真實的目標投入產出表，故進一步采用第二種比較方式對更新方法進行穩(wěn)健性比較。該比較過程首先設定某一更新方法為基礎方法，而后最小化基礎方法目標函數(shù)，以獲得的參數(shù)為依據(jù)，推導其他更新方法的目標函數(shù)，并與INO指標一起作為更新方法穩(wěn)健性評價指標。計算結果見表2。

表2 更新方法穩(wěn)健性比較 (單位:104）

表2統(tǒng)計指標數(shù)值中，所有統(tǒng)計指標數(shù)值均是越小越好。DCE-WLS法綜合得分排名第一，六項指標數(shù)值分別28.691、40.851、13.525、10.261、8.566和612.257，為5種更新方法均值的88.65%、91.03%、81.76%、80.26%、72.90%和73.10%，顯示了最優(yōu)的穩(wěn)健性。

4 結論

投入產出表是產業(yè)經濟研究的基礎，為了更好提升表格時效性和適用性，選擇合理的更新方法十分重要。本文從調查更新和數(shù)學更新兩個角度對現(xiàn)有投入產出表更新方法進行綜述，分析方法更新原理，總結方法優(yōu)缺點。在此基礎上，重點改進交叉熵類方法及最小二乘類方法，構造信息權重矩陣降低先驗信息損失度，引入零值約束確保有效繼承零值結構，鑒于投入產出表數(shù)據(jù)具體情況存在一定不確定性，采用加權方式設置組合式的DCE-WLS法。

為了驗證DCE-WLS法更新效果，選取GRAS、STAD、TLS、MCE作為比較方法，以STPE、RMSE、THeil U、MAE、WAD、SIM和INO為比較指標。分別采用兩種方式進行更新精準性和穩(wěn)健性比較，計算結果顯示DCE-WLS法排名均為第一，展現(xiàn)了更好的適用性。由于投入產出表是構成社會核算矩陣的核心，因此，DCE-WLS法也可延伸用于社會核算矩陣的更新工作。