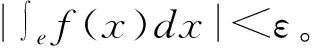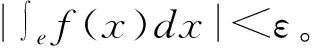Lebesgue測度的介值定理及其應(yīng)用
路慧芹,路婕
(山東師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 山東 濟(jì)南 250014)
1 引言
Lebesgue測度是建立Lebesgue積分的理論基礎(chǔ)。 在實(shí)變函數(shù)教科書中, 均給出了Lebesgue測度具有的一般性質(zhì), 如非負(fù)性、單調(diào)性、可列可加性等。 作為對Lebesgue外測度性質(zhì)的補(bǔ)充, 謝天夏等[1]研究了Lebesgue外測度可列可加性的充要條件,張?zhí)斓碌萚2]給出了中有界集的Lebesgue外測度具有介值性質(zhì)。 本文利用連續(xù)函數(shù)的介值性(參見文獻(xiàn)[3-5])及Lebesgue測度的單調(diào)性(參見文獻(xiàn)[6]),給出了RN中的任一可測集的Lebesgue測度均具有介值性質(zhì), 并把所得結(jié)果用來討論Lebesgue積分的性質(zhì), 證明了積分絕對連續(xù)性的逆命題也是成立的。
2 主要結(jié)果
定理1 設(shè)E為R1中的可測集,0 證明因?yàn)镋為R1中的可測集,故有E?(-∞,+∞),定義函數(shù) f(x)=m(E∩(-∞,x]),x∈(-∞,+∞)。 f(x2)=m(E∩(-∞,x2])≥m(E∩(-∞,x1])=f(x1), 且 f(x2)-f(x1) =m(E∩(-∞,x2])-m(E∩(-∞,x1]) =m((E∩(-∞,x1])∪(E∩(x1,x2])-m(E∩(-∞,x1]) ≤m(E∩(-∞,x1])+m(E∩(x1,x2])-m(E∩(-∞,x1]) =m(E∩(x1,x2])≤m((x1,x2])=x2-x1, 于是,我們有 |f(x2)-f(x1)|≤|x2-x1|,?x1,x2∈(-∞,+∞)。 因此,f(x)是(-∞,+∞)上的連續(xù)函數(shù),由連續(xù)函數(shù)的介值定理知,存在x0∈(-∞,+∞),使得f(x0)=c.令E1=E∩(-∞,x0],則有mE1=c。 定理2 設(shè)E為R2中的可測集,0 證明(1) 首先,我們證明:?ε>0,?半開區(qū)間I?R2,s.t.m(E∩I)>mE-ε。 (2)其次, 我們證明:對R2中任意的半開區(qū)間I=(a1,b1]×(a2,b2],定義二元函數(shù) f(x,y)=m(E∩((a1,x]×(a2,y])),(x,y)∈I, 則f(x,y)在I上連續(xù)。事實(shí)上,對任意的(x,y1)∈I,(x,y2)∈I,不妨設(shè)y1 f(x,y2)=m(E∩((a1,x]×(a2,y2]))≥m(E∩((a1,x]×(a2,y1]))=f(x,y1), 且 f(x,y2)-f(x,y1) =m(E∩((a1,x]×(a2,y2]))-m(E∩((a1,x]×(a2,y1])) =m(E∩((a1,x]×(y1,y2])) ≤m((a1,x]×(y1,y2]) ≤(b1-a1)(y2-y1)。 于是,我們有 |f(x,y2)-f(x,y1)|≤(b1-a1)|y2-y1|,?(x,y1)∈I,(x,y2)∈I。 同理可證,|f(x2,y)-f(x1,y)|≤(b2-a2)|x2-x1|,?(x1,y)∈I,(x2,y)∈I。 即,f(x,y)在I上對每一個(gè)變元都滿足李氏條件。對任意的(x,y)∈I,(x0,y0)∈I,我們有 |f(x,y)-f(x0,y0)| ≤|f(x,y)-f(x,y0)|+|f(x,y0)-f(x0,y0)| ≤(b1-a1)|y-y0|+(b2-a2)|x-x0|, 由此易知,f(x,y)在I上連續(xù)。 注:類似于定理2的證明過程,我們可以證明,對于RN(N>2)上的可測點(diǎn)集E的Lebesgue測度同樣具有類似于定理2的介值性定理。 于是我們有下述一般性結(jié)果。 定理3 (Lebesgue測度的介值定理) 設(shè)E為RN(N∈)中的可測集,0 所以,f(x)在E上可積。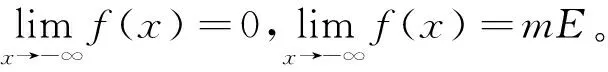

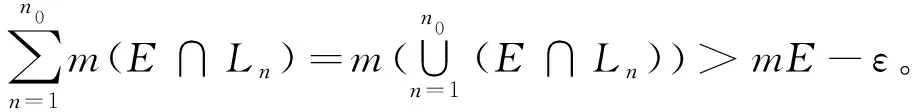
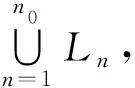
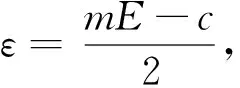
3 應(yīng)用