基于多分辨率和自適應(yīng)分?jǐn)?shù)階的Active Demons算法
張桂梅 郭黎娟 熊邦書 儲(chǔ) 珺
1(南昌航空大學(xué)計(jì)算機(jī)視覺研究所 南昌 330063) 2(南昌航空大學(xué)信息工程學(xué)院 南昌 330063)
數(shù)字圖像配準(zhǔn)[1]是指在不同時(shí)段、不同視角和不同傳感器下拍攝的2幅或者多幅圖像間的幾何變換關(guān)系的處理技術(shù).圖像配準(zhǔn)技術(shù)廣泛應(yīng)用于環(huán)境監(jiān)測(cè)、物體或者場(chǎng)景識(shí)別、醫(yī)學(xué)影像分析等與人類息息相關(guān)的各個(gè)方面.根據(jù)待配準(zhǔn)目標(biāo)的類型可以將圖像配準(zhǔn)分為剛性配準(zhǔn)和非剛性配準(zhǔn).剛性配準(zhǔn)方法適用于剛性目標(biāo)或者不存在變形的圖像配準(zhǔn),但在自然場(chǎng)景中目標(biāo)大多是非剛性的,所以需要采用非剛性圖像配準(zhǔn)方法來解決非剛性圖像配準(zhǔn)問題.非剛性圖像配準(zhǔn)方法主要可以分為基于空間變換的配準(zhǔn)方法和基于物理模型的配準(zhǔn)方法兩大類[2]:1)基于空間變換的非剛性配準(zhǔn)方法,采用圖像的空間變換來擬合圖像的變形.常用方法有多項(xiàng)式法[3]、小波基函數(shù)[4]、B樣條[5]等.2)基于物理模型的配準(zhǔn)方法是將待配準(zhǔn)圖像到參考圖像的形變過程視為一個(gè)物理變形,通過選擇合適的物理模型來擬合這種形變以達(dá)到配準(zhǔn)的目的.常用的模型有基于彈性力學(xué)理論的模型[6]、基于粘性流體的模型[7]以及基于光流場(chǎng)理論的模型[8-11].其中,基于光流場(chǎng)模型的非剛性配準(zhǔn)方法由于其較高的檢測(cè)精度和較好的穩(wěn)健性得到越來越多的重視.Thirion[8]提出基于光流場(chǎng)理論的Demons算法,該算法的基本思想是利用參考圖像梯度驅(qū)動(dòng)浮動(dòng)圖像中的每一個(gè)像素向參考圖像對(duì)應(yīng)的像素點(diǎn)移動(dòng).但是該算法只采用了參考圖像的梯度信息來驅(qū)動(dòng)浮動(dòng)圖像發(fā)生形變,當(dāng)梯度信息不足時(shí)容易產(chǎn)生誤配準(zhǔn).He等人[9]根據(jù)作用力和反作用力原理對(duì)Demons算法進(jìn)行改進(jìn),提出了允許參考圖像和浮動(dòng)圖像的梯度共同驅(qū)動(dòng)像素點(diǎn)向著對(duì)方對(duì)應(yīng)的像素點(diǎn)移動(dòng)的Active Demons配準(zhǔn)算法.Vercauteren等人[10]為了保證形變場(chǎng)的拓?fù)湫裕岢隽宋⒎滞週og Demons算法,其基本思想是將基于圖像灰度的Demons算法的配準(zhǔn)過程看成能量?jī)?yōu)化過程.Lorenzi等人[11]提出基于局部互相關(guān)相似性測(cè)度的微分同胚LCC Demons算法,該算法可以削弱灰度偏差對(duì)醫(yī)學(xué)圖像配準(zhǔn)的影響,具有更高的配準(zhǔn)精度.在臨床實(shí)際應(yīng)用中,準(zhǔn)確、有效和魯棒的圖像配準(zhǔn)可以避免醫(yī)學(xué)圖像中各種偏差引起的影響.由于存在的非剛性配準(zhǔn)算法對(duì)嚴(yán)重扭曲變形的圖像配準(zhǔn)精度和效率都比較低,張桂梅等人[12]提出基于Nystr?m低階近似和譜特征的圖像非剛性配準(zhǔn)算法,同時(shí)為了提高配準(zhǔn)精度,在該模型中加入了小波變換的多分辨率策略.Tang等人[13]在Active Demons中引入平衡系數(shù),將與彈性系數(shù)共同調(diào)節(jié)驅(qū)動(dòng)力的強(qiáng)度,在引入平衡系數(shù)的同時(shí)加入了多分辨率策略,既提高了配準(zhǔn)精度,也提高了收斂速度.但是以上這些方法的驅(qū)動(dòng)力都只是來源于圖像的灰度信息,這對(duì)于灰度均勻、弱邊緣和弱紋理的圖像配準(zhǔn)優(yōu)化容易陷入局部最小,從而降低配準(zhǔn)的精度.
分?jǐn)?shù)階微積分是整數(shù)階微積分的推廣,它不僅拓寬了階次的運(yùn)算范圍、豐富了微積分理論,而且比整數(shù)階微積分更靈活.在圖像處理領(lǐng)域,微積分理論已經(jīng)取得了初步的應(yīng)用.如Pu等人[14]和Chen等人[15]針對(duì)傳統(tǒng)的整數(shù)階微分去噪方法很容易導(dǎo)致邊緣和紋理細(xì)節(jié)模糊,提出了將分?jǐn)?shù)階微積分理論運(yùn)用于圖像去噪,實(shí)驗(yàn)結(jié)果表明,基于分?jǐn)?shù)階的圖像去噪算法提高了圖像的信噪比,而且對(duì)紋理的保持效果也有所提升.張桂梅等人[16]針對(duì)原始和各種擴(kuò)展的Demons算法對(duì)灰度均勻和弱紋理區(qū)域無效的問題,將R-L分?jǐn)?shù)階梯度應(yīng)用到Demons算法中,該算法驗(yàn)證了R-L分?jǐn)?shù)階微分能夠增強(qiáng)圖像灰度變化較大的梯度信息,提高了配準(zhǔn)精度和配準(zhǔn)速度.但是分?jǐn)?shù)階主動(dòng)Demons算法尋求圖像配準(zhǔn)效果最佳的階次時(shí),通常需要多次實(shí)驗(yàn)人工選取,費(fèi)時(shí)費(fèi)力,缺乏階次自適應(yīng).Li等人[17-18]根據(jù)整幅圖像的動(dòng)態(tài)梯度特征調(diào)整分?jǐn)?shù)階,用于圖像的增強(qiáng)和去噪,實(shí)驗(yàn)證明了該模型的有效性.張桂梅等人[19]針對(duì)RSF活動(dòng)輪廓模型在分割弱紋理、弱邊緣圖像時(shí),優(yōu)化易陷入局部極小導(dǎo)致曲線演化速度緩慢和局部擬合項(xiàng)的高斯核函數(shù)會(huì)導(dǎo)致目標(biāo)的邊界模糊的問題,提出了一種基于自適應(yīng)分?jǐn)?shù)階的活動(dòng)輪廓模型,實(shí)驗(yàn)表明,該方法的分割精度與分割效率都有較大的提高.
針對(duì)上述問題,本文在文獻(xiàn)[16]的基礎(chǔ)上做了一些新的工作:1)構(gòu)建了自適應(yīng)分?jǐn)?shù)階階次的數(shù)學(xué)模型.由于文獻(xiàn)[16]的最佳階次需要通過多次實(shí)驗(yàn)人工選取,費(fèi)時(shí)費(fèi)力.本文根據(jù)圖像的局部特征(圖像梯度模值和信息熵),構(gòu)建了自適應(yīng)分?jǐn)?shù)階階次的數(shù)學(xué)模型.該模型以反正切函數(shù)為原型,以圖像的梯度模值和信息熵為自變量,建立了微分階次與圖像局部信息之間的關(guān)系,從而可以根據(jù)圖像的局部信息特征自動(dòng)計(jì)算圖像中各個(gè)像素點(diǎn)的最佳階次,并將該模型應(yīng)用在Active Demons算法的圖像配準(zhǔn)中.2)為了提高配準(zhǔn)的效率,引入了多分辨率策略.采用下采樣將圖像進(jìn)行分層,先在最低分辨率層應(yīng)用較少的時(shí)間進(jìn)行粗配準(zhǔn),并將其配準(zhǔn)結(jié)果作為更高分辨率層的初始參數(shù),再在高分辨率下利用較多的時(shí)間來進(jìn)行精配準(zhǔn);逐層細(xì)化,按照由粗到精的方式執(zhí)行,從而提高圖像配準(zhǔn)精度和效率.
1 相關(guān)理論
1.1 Demons算法
為了補(bǔ)償時(shí)序圖像的2幅連續(xù)幀之間物體和視點(diǎn)的相對(duì)運(yùn)動(dòng),光流的概念被引入到了計(jì)算機(jī)視覺中.Thirion[8]提出基于光流場(chǎng)理論的Demons非剛性配準(zhǔn)算法,該算法的基本思想是將參考圖像S和浮動(dòng)圖像M看成是連續(xù)運(yùn)動(dòng)的圖像序列中的2幀,要完成圖像配準(zhǔn)的過程,即要找到1個(gè)驅(qū)動(dòng)力F,利用驅(qū)動(dòng)力驅(qū)動(dòng)浮動(dòng)圖像中的每一個(gè)像素向參考圖像對(duì)應(yīng)的像素點(diǎn)移動(dòng).假設(shè)圖像在運(yùn)動(dòng)過程中亮度保持恒定,根據(jù)光流場(chǎng)方程可以得到空間任意一點(diǎn)p(x,y)的形變向量u:

(1)

但是,當(dāng)參考圖像為灰度均勻圖像時(shí),參考圖像的灰度梯度就可能為0,此時(shí)容易造成u很不穩(wěn)定.基于此,在式(1)中添加1個(gè)外力,則有:

(2)
1.2 Active Demons算法
原始Demons算法只采用了參考圖像的梯度信息來驅(qū)動(dòng)浮動(dòng)圖像發(fā)生形變,但是當(dāng)圖像中灰度均勻、梯度信息不足時(shí),易產(chǎn)生誤配準(zhǔn),并且原始的Demons算法只適用于處理小形變圖像,對(duì)大形變圖像配準(zhǔn)效果較差.于是,He等人[9]根據(jù)牛頓第三定律,同時(shí)用參考圖像和浮動(dòng)圖像的梯度信息來驅(qū)動(dòng)形變,其中浮動(dòng)圖像的梯度信息作為一種正內(nèi)力,參考圖像的信息作為一種負(fù)內(nèi)力.于是就有:

(3)
由于引入了正內(nèi)力后,參考圖像和浮動(dòng)圖像的梯度則共同驅(qū)動(dòng)著對(duì)方對(duì)應(yīng)的像素點(diǎn)移動(dòng),所以可以有效地配準(zhǔn)大形變圖像.為了方便調(diào)整驅(qū)動(dòng)力強(qiáng)度,在式(3)上加入了均化系數(shù)β,于是有:

(4)
這樣可以通過改變?chǔ)碌闹悼刂菩巫兿蛄康拇笮。x擇合適的β值,既可以提高配準(zhǔn)的精確度,也可以加快收斂速度.
1.3 分?jǐn)?shù)階的Active Demons算法
原始和各種擴(kuò)展的Demons算法的驅(qū)動(dòng)力都只是來源于圖像的灰度信息,這對(duì)于灰度均勻、弱邊緣和弱紋理的圖像配準(zhǔn)無效或者優(yōu)化容易陷入極小.然而,分?jǐn)?shù)階微分既可以增強(qiáng)圖像的紋理細(xì)節(jié),又可以保留圖像的平滑區(qū)域信息.所以,文獻(xiàn)[16]將分?jǐn)?shù)階梯度代替了圖像的梯度,于是有:

(5)
其中,Hx(x,y,α)和Hy(x,y,α)是二維圖像x軸方向的分?jǐn)?shù)階微分掩模和y軸方向的分?jǐn)?shù)階微分掩模.
分?jǐn)?shù)階的Active Demons算法既提高了配準(zhǔn)精度,也加快了圖像配準(zhǔn)的速度.
2 本文算法
2.1 分?jǐn)?shù)階微分對(duì)信號(hào)的作用
以連續(xù)函數(shù)整數(shù)階的經(jīng)典定義為基礎(chǔ),將微積分的階次由整數(shù)擴(kuò)展到分?jǐn)?shù).對(duì)于任意一個(gè)平方可積分的信號(hào)f(t)∈2,其傅里葉變換為
(6)
將整數(shù)階信號(hào)擴(kuò)展到分?jǐn)?shù)階,則有階次為α的分?jǐn)?shù)階微積分形式:

(7)
當(dāng)α>0時(shí),Dα表示α階微分乘性算子;當(dāng)α<0時(shí),Dα表示α階積分乘性算子.其傅里葉變換為

(8)
其中:

(9)
根據(jù)式(9)繪制分?jǐn)?shù)階微積分幅頻曲線圖,如圖1所示.當(dāng)α<0時(shí),高頻信號(hào)有極大的衰減;同時(shí),低頻信號(hào)有一定程度的增強(qiáng).當(dāng)0<α<1時(shí),中高頻信號(hào)得到了增強(qiáng),其中中頻信號(hào)得到了較大的增強(qiáng),低頻信號(hào)沒有極大的衰減,而是進(jìn)行了非線性的保留.當(dāng)1<α<2時(shí),高頻信號(hào)得到了極大的增強(qiáng),然而低頻信號(hào)卻得到了極大的衰減.在圖像處理中,圖像的平滑區(qū)域?qū)儆诘皖l信號(hào),圖像的紋理細(xì)節(jié)屬于中頻信號(hào),圖像的邊緣和噪聲屬于高頻信號(hào).本文的目的是要解決灰度均勻、弱邊緣和弱紋理的圖像配準(zhǔn)問題,即既需要增強(qiáng)中頻信號(hào),又需要保留低頻信號(hào),同時(shí)結(jié)合幅頻特性可知,本文的分?jǐn)?shù)階階次宜選在0~1之間.分?jǐn)?shù)階階次的選定將為自適應(yīng)分?jǐn)?shù)階微分模型的構(gòu)建提供理論基礎(chǔ).

Fig. 1 The amplitude-frequency curve of fractional differentiator圖1 幅頻特性曲線圖
2.2 構(gòu)造R-L分?jǐn)?shù)階微分掩模
假設(shè)信號(hào)f(t)(t∈[a,b],a (10) 其中: (11) 將R-L分?jǐn)?shù)階微分進(jìn)行一階求導(dǎo)有: (12) 根據(jù)卷積定理,R-L分?jǐn)?shù)階微分定義可改寫為 (13) 將R-L分?jǐn)?shù)階微分的卷積形式進(jìn)行一階求導(dǎo),于是有: (14) (15) 對(duì)h(x,y,α)進(jìn)行x和y方向一階求導(dǎo),則可以得到二維圖像x軸方向的分?jǐn)?shù)階微分掩模Hx(x,y,α)和y軸方向的分?jǐn)?shù)階微分掩模Hy(x,y,α): (16) 實(shí)際上,圖像是數(shù)值有限的數(shù)字量,而且圖像灰度變化發(fā)生在最短距離的相鄰像素之間,所以需要將Hx(x,y,α)和Hy(x,y,α)進(jìn)行離散化: (17) 其中,xM=-K,-K+1,…,K-1,K,yM=-L,-L+1,…,L-1,L.Hx(x,y,α)和Hy(x,y,α)是(2K+1)×(2L+1)的微分掩模算子.將Hx(x,y,α),Hy(x,y,α)分別與圖像進(jìn)行卷積可以得到沿x軸和y軸方向的分?jǐn)?shù)階梯度,最終可以得到x軸和y軸方向的形變向量. 2.3.1 相關(guān)特性的選擇 由于本文是要解決灰度均勻、弱邊緣和弱紋理的圖像配準(zhǔn)問題,由圖1可知,當(dāng)選定階次在0~1之間時(shí),當(dāng)分?jǐn)?shù)階階次越小,低頻信號(hào)的增強(qiáng)程度越大,也即低頻信號(hào)的保留程度較大,所以在低頻區(qū)域應(yīng)該選取較小的分?jǐn)?shù)階階次;當(dāng)分?jǐn)?shù)階階次越大,中高頻信號(hào)的增強(qiáng)強(qiáng)度就越大,尤其是中頻信號(hào),所以在高頻區(qū)域應(yīng)該選取較大的分?jǐn)?shù)階階次.由于一幅圖像中通常都包含不同的頻率段,所以在選擇分?jǐn)?shù)階階次時(shí),不應(yīng)該是整幅圖像都選用同一個(gè)固定階次,而是應(yīng)該根據(jù)圖像的相關(guān)特性選擇不同的分?jǐn)?shù)階階次.圖像梯度和信息熵都可以反映圖像紋理信息的豐富情況,所以本文根據(jù)圖像梯度和圖像信息熵構(gòu)造自適應(yīng)模型,以此實(shí)現(xiàn)自動(dòng)為每個(gè)像素點(diǎn)都選取一個(gè)最佳的分?jǐn)?shù)階階次. 在圖像邊緣和紋理區(qū)域,圖像梯度較大;在圖像平滑區(qū)域,圖像梯度較小.圖像f是一個(gè)二維離散函數(shù),圖像梯度是對(duì)這個(gè)二維函數(shù)在點(diǎn)(x,y)處進(jìn)行求導(dǎo),于是有: (18) 其中,I為圖像的灰度,圖像的梯度模值為 (19) 圖像信息熵是信息量的一種度量方式,反映了圖像紋理豐富情況.在圖像邊緣和紋理區(qū)域,圖像信息熵較大;在圖像平滑區(qū)域,圖像信息熵較小.其定義為 (20) 其中,C為圖像信息熵,(i,j)為像素坐標(biāo),Ii j為灰度值,ω為模板,Pi j為在模板內(nèi)相同灰度值的概率. 2.3.2 構(gòu)造自適應(yīng)分?jǐn)?shù)階微分模型 在構(gòu)造自適應(yīng)分?jǐn)?shù)階函數(shù)時(shí),為了保證分?jǐn)?shù)階階次在0~1之間,將圖像的梯度模值和信息熵進(jìn)行歸一化,即0≤|G|≤1,0≤|C|≤1.然后將歸一化的圖像梯度模值和信息熵進(jìn)行融合,有: f(G,S)=m|G|+n|C|, 0≤f≤1, (21) 其中,m,n為權(quán)值,根據(jù)多次實(shí)驗(yàn)本文選取m=n=0.5. 由2.3.1節(jié)定義可知,當(dāng)f值越大,對(duì)中高頻區(qū)域的增強(qiáng)程度應(yīng)該較大;當(dāng)f值越小,那么對(duì)低頻區(qū)域的保留程度應(yīng)該較大.又由幅頻特性可知,階次在0~1之間,隨著分?jǐn)?shù)階階次的增大,中高頻信號(hào)的增強(qiáng)強(qiáng)度越來越大,低頻信號(hào)呈現(xiàn)非線性衰減;隨著分?jǐn)?shù)階階次的減小,中高頻信號(hào)呈現(xiàn)急速衰減,然而低頻信號(hào)卻得到了有效的非線性的保留.所以,對(duì)于中高頻區(qū)域,應(yīng)該選取較大的分?jǐn)?shù)階階次;對(duì)于低頻區(qū)域,應(yīng)該選取較小的分?jǐn)?shù)階階次.也即f值越大,所選取的分?jǐn)?shù)階階次應(yīng)該較大;f值越小,所選取的分?jǐn)?shù)階階次應(yīng)該較小.為了保證分?jǐn)?shù)階階次的選擇在0~1之間,本文選用反正切函數(shù)為原型函數(shù).自適應(yīng)函數(shù)定義為 α=k×arctanf+b, (22) 其中,α為分?jǐn)?shù)階階次;k,b為待定系數(shù).由于f=1時(shí),該像素點(diǎn)一定位于中高頻區(qū)域,此時(shí)應(yīng)該選取較大的分?jǐn)?shù)階階次,即α=1;f=0時(shí),該像素點(diǎn)一定位于低頻區(qū)域,此時(shí)應(yīng)該選取較小的分?jǐn)?shù)階階次,即α=0.于是就有: (23) 所以自適應(yīng)分?jǐn)?shù)階微分模型為 (24) 2.3.3 驗(yàn)證自適應(yīng)分?jǐn)?shù)階微分模型的有效性 為了驗(yàn)證自適應(yīng)分?jǐn)?shù)階微分模型的有效性,本節(jié)采用醫(yī)學(xué)圖像進(jìn)行實(shí)驗(yàn),如圖2所示,其中圖2(a)為參考圖像,圖2(b)為浮動(dòng)圖像.選用均方誤差(MSE)和峰值信噪比(PSNR)評(píng)價(jià)配準(zhǔn)的精度,MSE越小、PSNR越大,配準(zhǔn)精度越高.將本文模型與分?jǐn)?shù)階Active Demons算法進(jìn)行了比較,其實(shí)驗(yàn)結(jié)果如圖3、圖4和表1所示,其中圖3和圖4分別為均方誤差(MSE)與迭代次數(shù)的關(guān)系曲線圖、峰值信噪比(PSNR)與迭代次數(shù)的關(guān)系曲線圖,實(shí)驗(yàn)中分?jǐn)?shù)階Active Demons算法的分?jǐn)?shù)階階次選取3個(gè)效果較好階次即0.1,0.5,0.9.從圖3和圖4的實(shí)驗(yàn)結(jié)果可以看出,自適應(yīng)分?jǐn)?shù)階Active Demons算法的配準(zhǔn)曲線收斂速度更快,并且均方誤差和峰值信噪比在迭代100次的時(shí)候開始收斂,而分?jǐn)?shù)階Active Demons算法的均方誤差和峰值信噪比在迭代200次時(shí)仍然沒有收斂,即本文方法比分?jǐn)?shù)階Active Demons算法的效率更高.從表1中可以得出,自適應(yīng)分?jǐn)?shù)階Active Demons算法的配準(zhǔn)精度高于分?jǐn)?shù)階Active Demons算法.這是因?yàn)楸疚牡哪P褪歉鶕?jù)圖像的局部特征自適應(yīng)計(jì)算圖像中每個(gè)像素點(diǎn)的最佳階次,也即能確保在圖像的每個(gè)像素點(diǎn)上都取到最佳階次,且基于最佳階次構(gòu)造分?jǐn)?shù)階微分動(dòng)態(tài)模板,階次的選取更合理,所以配準(zhǔn)精度和配準(zhǔn)效率均能得到有效的提高. Fig. 2 Medical image圖2 醫(yī)學(xué)圖像 Fig. 3 The relation curve between MSE and iteration number圖3 均方誤差與迭代次數(shù)的關(guān)系曲線圖 Fig. 4 The relation curve between PSNR to noise ratio and iteration number圖4 峰值信噪比與迭代次數(shù)的關(guān)系曲線圖 Table 1 Comparison of Registration Accuracy BetweenTwo Algorithms 由于分?jǐn)?shù)階微分模板較整數(shù)階的計(jì)算更復(fù)雜,并且本文得到微分模板是基于最佳階次的動(dòng)態(tài)模板,所以構(gòu)造了自適應(yīng)分?jǐn)?shù)階微分模型的配準(zhǔn)時(shí)間相比于固定分?jǐn)?shù)階階次的配準(zhǔn)時(shí)間會(huì)有所增加.因此可以將多分辨率的分層配準(zhǔn)策略應(yīng)用到自適應(yīng)分?jǐn)?shù)階Active Demons配準(zhǔn)過程中,提高算法的運(yùn)行速度和避免局部極值.配準(zhǔn)按照由粗到精的方式運(yùn)行,在低分辨率下利用較少的時(shí)間進(jìn)行粗配準(zhǔn),在高分辨率下花銷較多的時(shí)間進(jìn)行精配準(zhǔn). 文獻(xiàn)[13]提出了多分辨率策略的圖像配準(zhǔn)算法,下采樣與小波變換相比,下采樣能夠提高信號(hào)的信噪比,它對(duì)信號(hào)進(jìn)行隔點(diǎn)采樣,將信息進(jìn)行了壓縮存儲(chǔ),從而提高了圖像配準(zhǔn)的速度和精度.本文考慮利用下采樣將實(shí)驗(yàn)圖像進(jìn)行2層分解,先在最低分辨率圖像上進(jìn)行配準(zhǔn),然后將當(dāng)層的配準(zhǔn)結(jié)果作為更高一級(jí)分辨率圖像配準(zhǔn)的初始參數(shù),直至配準(zhǔn)到最高分辨率圖像(原始圖像). Fig. 5 Flow chart of our algorithm圖5 本文算法流程圖 算法1. 基于多分辨率和自適應(yīng)分?jǐn)?shù)階的Active Demons算法. Step1. 輸入?yún)⒖紙D像和浮動(dòng)圖像; Step2. 用下采樣將參考圖像和浮動(dòng)圖像進(jìn)行2層分解; Step3. 選取相同層的浮動(dòng)圖像和參考圖像; Step4. 根據(jù)圖像梯度模值和信息熵構(gòu)建自適應(yīng)分?jǐn)?shù)階微分模型α=4/π×arctanf; Step5. 根據(jù)式(24)計(jì)算每個(gè)像素點(diǎn)的最佳階次,基于此,再根據(jù)式(17)計(jì)算每個(gè)像素點(diǎn)的R-L分?jǐn)?shù)階微分動(dòng)態(tài)掩模; Step6. 根據(jù)式(5)求得形變向量u; Step7. 用高斯濾波器平滑配準(zhǔn)后的變形場(chǎng),主要是因?yàn)榕錅?zhǔn)后的變形場(chǎng)不能滿足平滑性要求; Step8. 判斷是否到最后一層,如果不是,返回Step3,進(jìn)入下一層圖像配準(zhǔn);否則配準(zhǔn)結(jié)束. 其算法步驟流程圖如圖5所示. Fig. 6 The result of Lena image registration圖6 Lena圖像配準(zhǔn)結(jié)果圖 本文實(shí)驗(yàn)所采用的計(jì)算機(jī)實(shí)驗(yàn)環(huán)境為:計(jì)算機(jī)配置為Pentium?Dual-Core CPU E6700 @3.20 GHz,內(nèi)存2.00 GB,32 b的Widows 7.0版本操作系統(tǒng),程序采用R2010a版Matlab實(shí)現(xiàn).圖像配準(zhǔn)中常用的評(píng)價(jià)標(biāo)準(zhǔn)有客觀評(píng)價(jià)和主觀評(píng)價(jià),其中主觀評(píng)價(jià)就是我們用肉眼觀察到配準(zhǔn)后圖像與參考圖像的相似程度,客觀評(píng)價(jià)就是用相似性度量來判斷配準(zhǔn)結(jié)果的好壞,常用的相似性度量有均方誤差(MSE)、峰值信噪比(PSNR)、互相關(guān)系數(shù)(CC)、圖像信息熵(C)等.本文主要采用主觀評(píng)價(jià)、均方誤差(MSE)和峰值信噪比(PSNR)來評(píng)價(jià)配準(zhǔn)結(jié)果的好壞. 為驗(yàn)證本文算法的有效性,本文采用Lena圖像、Brain圖像和變形Baboon圖像進(jìn)行實(shí)驗(yàn),由于本文算法是在分?jǐn)?shù)階Active Demons算法上進(jìn)行改進(jìn)的,所以將本文算法與分?jǐn)?shù)階Active Demons算法實(shí)驗(yàn)效果較好的2個(gè)固定階次進(jìn)行比較.又由于分?jǐn)?shù)階Active Demons算法是在Active Demons算法上改進(jìn)的,所以也將本文算法與Active Demons算法進(jìn)行比較. 3.2.1 Lena圖像實(shí)驗(yàn) 本次實(shí)驗(yàn)采用圖6(a)所示的Lena圖像作為參考圖像,圖6(b)作為浮動(dòng)圖像,參考圖像和浮動(dòng)圖像最大的差別就是Lena的臉部和帽子發(fā)生了變形.然后分別用本文算法、分?jǐn)?shù)階Active Demons算法和Active Demons算法進(jìn)行實(shí)驗(yàn),其實(shí)驗(yàn)結(jié)果如圖6所示.其中圖6(c)為Active Demons算法配準(zhǔn)結(jié)果圖,圖6(d)和圖6(e)分別為分?jǐn)?shù)階Active Demons算法在2個(gè)較佳階次α分別為0.4和0.8的配準(zhǔn)結(jié)果圖,圖6(f)為本文算法配準(zhǔn)結(jié)果圖.從圖6可以看出,圖6(c)的眉毛和帽檐的變形沒有得到有效矯正,圖6(d)和圖6(e)的配準(zhǔn)結(jié)果差不多,雖然帽子和眉毛處的配準(zhǔn)很成功,但是圖像最底部和頭發(fā)部分出現(xiàn)了信息丟失現(xiàn)象.從圖6(f)來看,其配準(zhǔn)結(jié)果很理想,既矯正了變形,也沒有出現(xiàn)信息丟失的情況.為了進(jìn)一步驗(yàn)證本文算法的有效性,本文也進(jìn)行了定量分析,實(shí)驗(yàn)結(jié)果如表2所示.從表2可以看出,本文算法的效果最好,這是因?yàn)楸疚氖紫雀鶕?jù)圖像的局部特征構(gòu)造了自適應(yīng)分?jǐn)?shù)階階次的數(shù)學(xué)模型,使得在圖像中每個(gè)像素點(diǎn)均能獲得最佳階次;其次引入了多分辨率的配準(zhǔn)策略,即在低分辨率下進(jìn)行了粗配準(zhǔn),將其得到的結(jié)果作為更高分辨率圖像配準(zhǔn)的輸入,在高分辨率下進(jìn)行精配準(zhǔn),所以本文的算法在圖像配準(zhǔn)的精度和效率都具有一定的優(yōu)勢(shì). Table 2 Comparison of Registration Accuracy BetweenDifferent Algorithms 3.2.2 醫(yī)學(xué)圖像實(shí)驗(yàn) 本次實(shí)驗(yàn)采用圖7(a)所示的Brain圖像作為參考圖像,圖7(b)作為浮動(dòng)圖像,參考圖像和浮動(dòng)圖像最大差別的地方就是中間部位和最底部(圖7中矩形及圓圈標(biāo)記處),參考圖像最底部沒有1個(gè)小黑點(diǎn),而浮動(dòng)圖像最底部明顯有1個(gè)小黑點(diǎn).其中圖7(c)為Active Demons算法配準(zhǔn)結(jié)果圖,圖7(d)和圖7(e)分別為分?jǐn)?shù)階Active Demons算法在2個(gè)較佳階次α分別為0.5和0.9的配準(zhǔn)結(jié)果圖,圖7(f)為本文算法配準(zhǔn)結(jié)果圖.從圖7可以看出,圖7(c)中間部位與浮動(dòng)圖像的中間部位差不多,并且配準(zhǔn)圖像的最底部與浮動(dòng)圖像一樣還有1個(gè)小黑點(diǎn),這并不接近參考圖像;圖7(d)中間黑色部位得到了加深,中上黑色部位有所擴(kuò)大,中下部分那黑色的2點(diǎn)不再是連著的,比較接近參考圖像,但是2個(gè)小黑點(diǎn)上方部位有一黑色橫條,而參考圖像中并沒有這一黑色橫條,而且配準(zhǔn)圖像的最底部也有1個(gè)小黑點(diǎn);圖7(e)中間部位相對(duì)于浮動(dòng)圖像來說,黑色部位有所擴(kuò)大,但是還并沒有接近參考圖像,而且圖像最底部仍然有1個(gè)小黑點(diǎn);圖7(f)中間黑色部位顏色就沒有那么深,黑色部位形狀也比較接近參考圖像,中下部位也沒有多出黑色橫條,而且配準(zhǔn)圖像最底部沒有了小黑點(diǎn),所以本文算法配準(zhǔn)的結(jié)果較好.為了進(jìn)一步驗(yàn)證本文算法的有效性,本文比較了各種方法的均方誤差(MSE)和峰值信噪比(PSNR),如表3所示.從表3可以看出,由本文算法配準(zhǔn)后的圖像,其均方誤差和峰值信噪比都比較理想,這是因?yàn)楸疚乃惴ㄔ诿總€(gè)像素點(diǎn)上都獲得了最佳的階次,在圖像的高頻區(qū)域,選取了較大的分?jǐn)?shù)階階次,在低頻區(qū)域,選取了較小的分?jǐn)?shù)階階次,故本文算法的配準(zhǔn)效果比較理想. Fig. 7 The result of Brain image registration圖7 Brain圖像配準(zhǔn)結(jié)果圖 Table 3 Comparison of Registration Accuracy BetweenDifferent Algorithms 3.2.3 變形Baboon圖像實(shí)驗(yàn) 本次實(shí)驗(yàn)采用紋理比較豐富的變形Baboon圖像進(jìn)行實(shí)驗(yàn),其中圖8(a)為參考圖像,圖8(b)為浮動(dòng)圖像,浮動(dòng)圖像相對(duì)于參考圖像是Baboon圖像大部分部位發(fā)生了變形,而且圖像周圍出現(xiàn)了波浪變形.分別用本文算法、分?jǐn)?shù)階Active Demons算法和Active Demons算法進(jìn)行實(shí)驗(yàn),其實(shí)驗(yàn)結(jié)果如圖8所示.其中圖8(c)為Active Demons算法配準(zhǔn)結(jié)果圖,圖8(d)和圖8(e)分別為分?jǐn)?shù)階Active Demons算法在2個(gè)較佳階次α分別為0.4和0.7的配準(zhǔn)結(jié)果圖,圖8(f)為本文算法配準(zhǔn)結(jié)果圖.從圖8可以看出,圖8(c)的中間部位基本不存在變形了,但是其周圍的波浪變形還沒有完全矯正,而且圖像變亮;圖8(d)基本上沒有變形區(qū)域了,只是圖像底部的波浪變形的矯正還有所欠缺;而圖8(e)的配準(zhǔn)結(jié)果相比前2個(gè)有所改善,所有的變形都得到了較有效的矯正;從圖8(f)可知,圖像得到了更好的矯正,但是圖像變得稍微模糊,這主要是因?yàn)楸疚乃惴ㄖ屑尤肓硕喾直媛逝錅?zhǔn)策略,該策略會(huì)丟失某部分信息,所以圖8(f)的結(jié)果會(huì)相對(duì)模糊.同理我們計(jì)算了各種算法配準(zhǔn)結(jié)果的均方誤差和峰值信噪比,其結(jié)果如表4所示. 從表4可以看出,本文算法的MSE和PSNR并不是最好的,但它與最好的結(jié)果相差不大,與未配準(zhǔn)的MSE和PSNR相比,本文的MSE和PSNR還是得到了很大的提高.總之,本文算法的配準(zhǔn)結(jié)果比較理想. Fig. 8 The result of Baboon image registration圖8 Baboon圖像配準(zhǔn)結(jié)果圖 Table 4 Comparison of Registration Accuracy BetweenDifferent Algorithms 3.2.4 配準(zhǔn)效率實(shí)驗(yàn) 本文從收斂速度和配準(zhǔn)時(shí)間2方面對(duì)配準(zhǔn)的效率進(jìn)行評(píng)價(jià),分別使用了Lena圖像、Brain圖像和變形Baboon圖像進(jìn)行了實(shí)驗(yàn).其中圖9、圖10和圖11分別是Lena圖像、Brain圖像和變形Baboon圖像的均方誤差與迭代次數(shù)的曲線圖,從曲線圖可看出,本文算法的結(jié)果在迭代20次時(shí)就開始收斂,其他算法最少在迭代60次時(shí)才開始收斂,即本文算法的收斂速度是最快的. Fig. 9 Iterative curve of Lena image圖9 Lena圖像迭代曲線圖 由于尋找分?jǐn)?shù)階Active Demons算法的最佳階次比較費(fèi)時(shí)費(fèi)力,所以本文在此基礎(chǔ)上構(gòu)造了自適應(yīng)分?jǐn)?shù)階微分模型.本部分將對(duì)分?jǐn)?shù)階Active Demons Fig. 10 Iterative curve of Brain image圖10 Brain圖像迭代曲線圖 Fig. 11 Iterative curve of Baboon image圖11 變形Baboon圖像迭代曲線圖 算法和本文算法的配準(zhǔn)時(shí)間進(jìn)行比較,本次實(shí)驗(yàn)圖像仍然為L(zhǎng)ena圖像、Brain圖像和變形Baboon圖像.本實(shí)驗(yàn)的目的主要是測(cè)試本文算法在配準(zhǔn)時(shí)間上是否具有優(yōu)越性,其結(jié)果如表5所示.從表5可以看出,本文算法的配準(zhǔn)時(shí)間是最多的,這是因?yàn)楸疚乃惴ㄖ屑尤肓俗赃m應(yīng)分?jǐn)?shù)階微分模型,計(jì)算了圖像中每個(gè)像素點(diǎn)的最佳階次,隨之構(gòu)造了動(dòng)態(tài)的R-L分?jǐn)?shù)階微分掩模;而基于分?jǐn)?shù)階的Active Demons算法人工選取了1個(gè)固定的分?jǐn)?shù)階階次,整幅圖像也只對(duì)應(yīng)1個(gè)R-L分?jǐn)?shù)階微分模板;所以,本文算法的配準(zhǔn)時(shí)間會(huì)比固定1個(gè)分?jǐn)?shù)階階次的配準(zhǔn)時(shí)間要更多.但是運(yùn)用分?jǐn)?shù)階的Active Demons算法來尋找1個(gè)較好階次的過程中,需要通過多次實(shí)驗(yàn)尋找最佳階次,即每次都需要更換1個(gè)分?jǐn)?shù)階階次重復(fù)進(jìn)行實(shí)驗(yàn).假設(shè)階次從0.1~0.9需要做9次實(shí)驗(yàn),這樣加起來的總時(shí)間會(huì)比本文算法的配準(zhǔn)時(shí)間多很多.綜上所述,本文算法在配準(zhǔn)時(shí)間上具有一定的優(yōu)越性,且不需要通過多次實(shí)驗(yàn)不停地尋找最佳階次,實(shí)現(xiàn)了分?jǐn)?shù)階階次的最適應(yīng)計(jì)算. Table 5 Time Comparison of Two Methods表5 2種算法的時(shí)間對(duì)比 s 將自適應(yīng)R-L分?jǐn)?shù)階微分引入到圖像配準(zhǔn)中,能解決灰度均勻和弱紋理區(qū)域的圖像配準(zhǔn).本文基于圖像的梯度模值和信息熵,以反正切函數(shù)為原型,構(gòu)造了自適應(yīng)分?jǐn)?shù)階階次的數(shù)學(xué)模型,自動(dòng)自適應(yīng)計(jì)算整幅圖像中各個(gè)像素點(diǎn)的階次,該方法可以根據(jù)圖像中每個(gè)像素點(diǎn)的局部特征信息自適應(yīng)調(diào)節(jié)算子模板系數(shù),對(duì)每個(gè)像素點(diǎn)分別應(yīng)用相應(yīng)的模板進(jìn)行處理,有效地解決人工尋求最佳分?jǐn)?shù)階階次的費(fèi)時(shí)費(fèi)力問題;此外,將多分辨率策略引入到自適應(yīng)分?jǐn)?shù)階Active Demons算法中,從而提高了圖像配準(zhǔn)的精度和效率.本文的方法可以用于灰度均勻和弱紋理區(qū)域的非剛性圖像配準(zhǔn),并能提高配準(zhǔn)的精度和效率,是Active Demons算法應(yīng)用的重要延伸.不足之處是本文自適應(yīng)數(shù)學(xué)模型的建立僅考慮了圖像的梯度模值和信息熵,所以該模型并不是最優(yōu)的模型.今后的研究工作將進(jìn)一步優(yōu)化自適應(yīng)數(shù)學(xué)模型,提高計(jì)算速度,進(jìn)而提高配準(zhǔn)效率.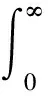







2.3 自適應(yīng)分?jǐn)?shù)階微分模型的構(gòu)造








2.4 基于多分辨率策略的圖像配準(zhǔn)

2.5 本文模型的配準(zhǔn)算法步驟
3 仿真實(shí)驗(yàn)
3.1 實(shí)驗(yàn)環(huán)境和評(píng)價(jià)準(zhǔn)則

3.2 實(shí)驗(yàn)結(jié)果和分析









4 結(jié) 論

