AAH不動點定理與二階非線性方程的正解
徐厚生, 王 波
(1. 沈陽建筑大學 理學院, 沈陽 110168; 2. 東北大學 理學院, 沈陽 110819)
0 引 言
一些學者已經開始應用泛函形式的錐拉伸與壓縮不動點定理研究非線性微分方程正解的存在性[1-15],文獻[2]將Leggett-Williams不動點定理[5]進行推廣, 得到如下結論。
引理1[2]設P是實Banach空間E上的錐,α是P上的非負連續凹泛函,β是P上的非負連續凸泛函,T:P→P是全連續算子。 若存在非負實數a,b,c,d使得
1) {x∈P|a<α(x),β(x) 2) 若x∈P, 有β(x)=b, 且α(x)≥a, 則β(Tx) 3) 若x∈P, 有β(x)=b, 且α(Tx) 4) {x∈P|c<α(x),β(x) 5) 若x∈P, 有α(x)=c, 且β(x)≤d, 則α(Tx)>c; 6) 若x∈P, 有α(x)=c, 且β(Tx)>d, 則α(Tx)>c; 且如果 a) 如果a b) 如果c Anderson等[2]應用引理1,討論了二階非線性邊值問題 (1) 正解的存在性。本文分別在壓縮條件和拉伸條件下, 通過引理1給出了二階非線性邊值問題 (2) 存在正解的充分條件。設G(t,s)是(2)相應齊次方程的Green函數, 即 (3) 引理2 由(3)表示的Green函數G(t,s)具有以下性質: G(t,s)在[0,1]×[0,1]上連續對稱; G(t,s)≥0,G(t,s)≤G(s,s), ?0≤t,s≤1; G(t,s)≥2tG(1/2,s),t∈[0,1/2],s∈[0,1]。 證明 前2個性質是顯然的。至于第3個性質, 事實上, 從而 G(t,s)≥2tG(1/2,s),t∈[0,1/2],s∈[0,1] 定義P={x∈C[0,1]|x(t)≥0,x是對稱的,x是凹的,t∈[0,1],x(t)≥2t‖x‖, t∈[0,1/2]}。易見P是C[0,1]中的錐。下面定義算子T為 易證P→7P。 設τ∈(0,1), 下面在P上定義凹泛函α為 凸泛函β為 由于x是凹的, 則 定理1 若b,c為正實數,3b≤c,f:[0,+∞)→[0,+∞)連續且滿足 2)f(ω)在[0,bτ]是單調遞減的, 在ω∈[bτ,b]有f(bτ)≥f(ω); 則方程(2)在P(β,α,b,c)中有一個正解x*。 ?x∈P有 1) 若?x∈P(α,c)={x∈P|α(x)≤c},則 則P(α,c)有界。 xM∈P(β,α,b,c) 事實上, 因此xM是凹的。 xM(t)=xM(2t·1/2)≥2t·xM(1/2)=2t‖xM‖ 故xM∈P。 則P(β,α,b,c)≠?。 xL∈{x∈P|a<α(x),β(x) 事實上, 由xM∈P, 同理可知xL∈P, 則{x∈P|a<α(x),β(x) xJ∈{x∈P|c<α(x),β(x) 事實上, 由xM∈P, 同理可知xJ∈P, 則{x∈P|c<α(x),β(x) 3) 若x∈P,β(x)=b,α(x)≥a, 則β(Tx) 事實上, 由于x的對稱性及連續性, 因此 從而 4) 若x∈P,β(x)=b,α(Tx) 事實上, 5) 若x∈P,α(x)=c,β(x)≤d, 則α(Tx)>c。 事實上, ?s∈[τ,1-τ],α(x)≤x(s)≤β(x) 6) 若x∈P,α(x)=c,β(Tx)>d, 則α(Tx)>c。 事實上, 根據引理1, 則方程在P(β,α,b,c)中有一個正解x*。 例1 令b=1,c=3,τ=1/4。函數 滿足條件: 根據定理1,方程(2)在P(β,α, 1, 3)中有一個正解。 定理2 若a,d為正實數,a≤τd,f:[0,+∞)→[0,+∞)連續且滿足: 2)f(ω)在[0,a]是單調遞減的, 在ω∈[a,b]有f(ω)≤f(a); 則方程(2)在P(α,β,a,d)中有一個正解x*。 ?x∈P有 1) 若?x∈P(β,d)={x∈P|β(x)≤d},則‖x‖=β(x)≤d,則P(β,d)有界。 若?x∈P(α,a)={x∈P|α(x)≤a}, 則 從而P(α,a)?P(β,d)。 xM∈{x∈P|a<α(x),β(x) 事實上, 從而xM是凹的。 故xM∈P。 則{x∈P|a<α(x),β(x) xL∈{x∈P|a<α(x),β(x) 事實上,由xM∈P, 同理可知xL∈P, 則{x∈P|a<α(x),β(x) xJ∈{x∈P|c<α(x),β(x) 事實上, 同理xJ∈P, 則x∈Pc<α(x),β(x) 3) 若x∈P,β(x)=b,α(x)≥a, 則β(Tx) 事實上, 則a≤x(s)≤b。 由于x的對稱性及連續性, 因此 從而 4) 若x∈P,β(x)=b,α(Tx) 事實上, 5) 若x∈P,α(x)=c,β(x)≤d, 則α(Tx)>c。 事實上, ?s∈[τ,1-τ],α(x)≤x(s)≤β(x) 則c≤x(s)≤d。 6) 若x∈P,α(x)=c,β(Tx)>d, 則α(Tx)>c。 事實上, 則根據引理1,方程在P(α,β,a,d)中有一個正解x*。 例2 令a=1,d=4,τ=1/4。函數 滿足條件: 2)f(ω)在[0,1]是單調遞減的,在[1,16]上有f(1)≥f(ω); 根據定理2,方程(2)在P(α,β,1,4)中有一個正解。 本文應用建立在錐理論和不動點指數方法基礎上的AAH不動點定理, 研究一類中與文獻中不同類型的二階非線性邊值問題正解的存在性。當非線性項滿足單調性和某些不等式條件時, 給出該類二階非線性邊值問題正解存在的錐拉伸與壓縮型充分條件, 并且通過一些例子來說明結論的應用。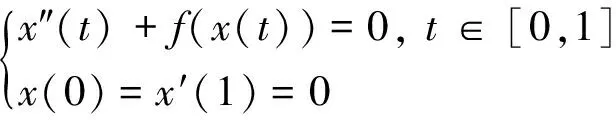





1 主要結論












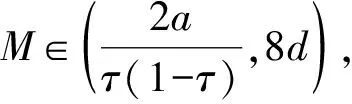



2 結 語