巧解“最短距離”問題

（合肥五十中新校 安徽合肥 230000）

先看這類問題最基本的例子：

要在河邊修一個水泵站向A、B兩個村莊供水（如圖1），村莊A、B在河道兩側，那么水泵站應該建在什么地方，才能使它到A、B兩個村莊的距離之和最小？

分析：這個問題可以直接應用基本事實“兩點之間，線段最短”來解決，連接AB交于點P（如圖2），此時AP+BP=AB，故點P就是應該建水泵站的位置。

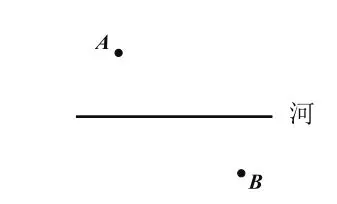
圖1

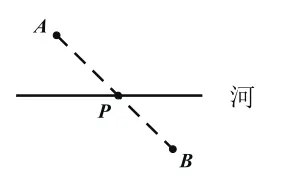
圖2

下面來看這個問題的一些變式。

一、利用軸對稱進行轉化并求最短距離

例1 如圖3，點A、B在直線l的同側，在直線直線l上求作一點P，使得AP+BP最小.

分析 解決這個問題的關鍵是將同側的兩點轉化為異側的兩點，就可以運用“兩點之間線段最短”來找到使距離最短的點。利用軸對稱的知識，若作點A關于直線l的對稱點A’（如圖4），則直線l上任意一點到A和A’的距離相等，點A、B到直線l上一點距離之和最短問題就轉化為A’、B到直線l上一點距離之和最短的問題，也就是我們最開始看到的基本問題。

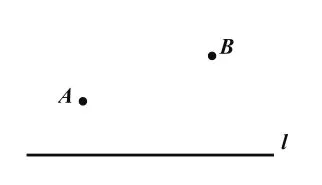
圖3

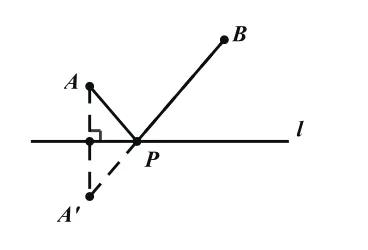
圖4

解：如圖4，作點A關于直線l的對稱點A’，連接A’B交直線l于點P，則點P即為所求做，此時AP+BP最小.

例2 如圖5，牧區內有一家牧民，點A處有一個馬廄，點B處是他的家.l1是草地的邊沿，l2是一條筆直的河流。每天，牧民要從馬廄牽出馬來，先去草地上讓馬吃草，再到河邊飲馬，然后回到家B處.請為牧民設計一條最短路線。

圖5

分析 我們需要在l1上找到一點M，在l2上找到一點N，使得AM+MN+BN最小，若作點A關于直線l1的對稱點A′，點B關于直線l2的對稱點B′（如圖6），則根據軸對稱的性質A’M=AM，B’N=BN，要使得AM+MN+BN最小，只要讓A’M+MN+B’N最小即可，這便轉化成了“兩點之間距離最短”的問題。

解：作點A關于直線l1的對稱點A′，點B關于直線l2的對稱點B′，連接A′B′交l1于點M，交l2于點N，則A→M→N→B的路程最短.

練習1 （2012·蘭州中考）如圖7，四邊形ABCD中，∠BAD=120°，∠B=∠D=90°，在BC、CD上分別找一點M、N，使△AMN周長最小時，求∠AMN+∠ANM的度數.

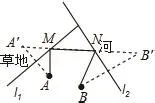
圖6

圖7

二、利用平面展開進行轉化并求最短距離

例3 如圖8，有一個長方體盒子，長4，寬2，高8，盒子的A點處有一只壁虎，B點處有一只蒼蠅，壁虎想沿著長方體盒子地表面去捕捉蒼蠅，請你計算出壁虎爬行的最短距離.所有

分析 若能將A點和B點放到一個平面內，問題就轉化成我們熟悉的“兩點之間線段最短”的問題了。

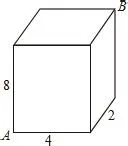
圖8

思考：怎樣將A點和B點放到一個平面呢？有幾種不同的方案？哪種方案最佳呢？

解：展開長方體的側面（如圖9），連接AB.

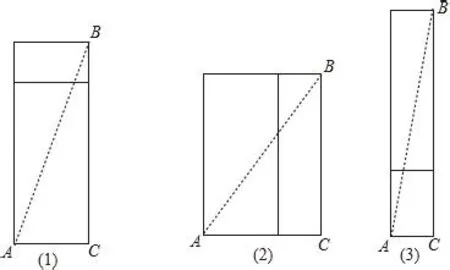
圖9

練習2 如圖10是一個圓柱形儲油罐，底面半徑為2米，高為5米，在底部A處準備修一個繞油罐的螺旋式樓梯到達位于上底面B處，則樓梯至少多長？

圖10

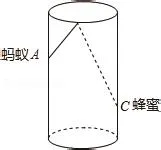
圖11

練習3 （2012·青島中考）如圖11，圓柱形玻璃杯，高為12cm，底面周長為18cm，在杯內離杯底3cm的點C處有一滴蜂蜜，此時一只螞蟻正好在杯外壁，離杯上沿4cm與蜂蜜相對的點A處，求螞蟻到達蜂蜜的最短距離.