CAWOA-ELM混合模型的鍋爐NOx排放量預測
賴 敏, 陳國彬, 劉 超, 牛培峰
(1.重慶工程學院 軟件學院,重慶 400056;2.重慶工商大學 融智學院,重慶 400033; 3. 燕山大學 電氣工程學院,河北秦皇島 066004)
隨著經濟發展和工業化進程的加速,我國大氣污染的形勢日益嚴峻。電廠是大氣污染物NOx的主要排放源[1]。因此,建立有效的NOx排放量預測模型不僅能優化電站鍋爐燃燒,而且對減少大氣污染至關重要。然而,鍋爐燃燒系統中NOx的形成是一個復雜的物理、化學過程,受煤種和配風方式等多種因素的影響[2],這些變量相互耦合,難以用機理模型描述這些復雜過程,機器學習技術的出現為鍋爐燃燒優化模型的建立提供了一條有效途徑[3-4]。
極限學習機(ELM)是依據Moore-Penrose(MP)廣義逆矩陣理論產生的一種新型有效的機器學習技術[5]。在ELM中,神經元權值中的輸入權值和隱層閾值隨機給定,然后通過正則化原則計算輸出權值,ELM網絡依然能逼近任意連續系統。與神經網絡和支持向量機相比,ELM優勢在于極大地提高了網絡的學習速度,已經受到越來越多的關注[6-7],因此可以采用ELM進行鍋爐NOx排放量的回歸預測。
ELM回歸方法的輸入權值和隱層閾值隨機給定,無任何先驗經驗可尋,往往容易造成回歸模型的泛化能力與穩定性不理想等問題。在實際應用過程中,為了達到理想的誤差精度,ELM通常需要調整輸入權值和隱層閾值,其調整過程可以轉化為最優化問題。因此,提出一種Sin混沌自適應鯨魚優化算法(CAWOA) 來優化ELM模型的參數,以改善該模型的穩定性和泛化能力,并進一步提出CAWOA-ELM的NOx排放量軟測量模型(以下簡稱CAWOA-ELM模型)。筆者以某330 MW煤粉鍋爐為研究對象,利用集散控制系統(DCS)中穩態樣本訓練集建立NOx排放量離線預測模型,利用該模型對未來穩態工況進行仿真預測,并驗證了CAWOA-ELM模型的有效性,為NOx排放量的精確預測以及熱電廠燃燒優化的推廣提供了一種有效手段。
1 混沌自適應鯨魚優化算法
1.1 鯨魚優化算法
鯨魚優化算法(WOA)是受鯨魚泡泡網覓食行為啟發,在2016年提出的一種新型群智能優化算法[8],并受到眾多研究者的關注[9-10]。為了從數學上描述鯨魚的泡泡網覓食行為,在WOA算法中設計了2種不同方式:收縮包圍機制和螺旋更新位置。
(1)收縮包圍機制。
設WOA算法種群個數為N,第i只鯨魚表示為Xi=(xi1,xi2,…,xid),i=1,2,…,N,其中d表示優化空間的維度。假設獵物位置Xp為當前種群中最優解,鯨魚個體X(t)均向最優解包圍,數學模型描述如下:
X(t+1)=Xp(t)-A·|CXp(t)-X(t)|
(1)
A=2a×r1-a
(2)
C=2×r2
(3)
a=2-2×t/Tmax
(4)
式中:t為當前迭代次數;A和C為系數向量;r1和r2為[0,1]內的隨機數;a為控制參數;Tmax為最大迭代次數。
收縮包圍機制通過式(1)和式(4)隨著控制參數a的減小而實現。
(2)螺旋更新位置。
鯨魚螺旋式運動捕獲食物的數學模型如下:
X(t+1)=Xp(t)+D′·ebl·cos(2πl)
(5)
式中:D′=|Xp(t)-X(t)|,為鯨魚與獵物之間的距離;b為一個常數,用來定義對數螺線的形狀;l為[-1,1]內的隨機數。
鯨魚的收縮包圍機制與螺旋更新位置是一種同步行為,通常按照概率值Pi=0.5選擇更新方式:若p WOA算法在處理復雜優化問題時存在收斂精度較低且易陷入局部最優的不足。為解決上述不足,提出CAWOA算法來改善WOA算法的全局優化能力。在WOA算法的基礎上,引入Logistic混沌搜索策略,通過對當前最優解進行混沌擾動以解決局部收斂的問題;此外,在位置更新中引入自適應慣性權值,通過平衡開發與探索能力解決算法收斂精度低的問題。 1.2.1 Sin混沌搜索策略 混沌映射是由確定性方程得到的具有隨機性的運動狀態,具有相空間的遍歷性和內在的隨機性,結合混沌變量進行優化搜索能有效跳出局部最優,實現全局優化。楊海東等[11]驗證了Sin混沌比Logistic混沌具有更明顯的混沌特性,針對WOA算法處理復雜函數優化問題陷入局部最優的不足,采用Sin混沌搜索對WOA算法每一代種群的最優個體(精英個體)進行M次混沌搜索,如果搜索到更優個體則進行取代,使其跳出局部最優,有效地避免了WOA算法陷入局部最優。Sin混沌映射模型定義如下: Zt+1=sin(2/Zt),t=0,1,…,N -1≤Zt≤1,Zt≠0 (6) 混沌映射的迭代計數器用t來計數,進行M次混沌迭代,系統輸出將遍歷整個解空間。 假設WOA算法種群中最優個體為Xi,在可行域內混沌優化過程為: (7) 假設WOA算法第i代的精英解是Xi=(xi1,xi2,…,xiD),Sin混沌搜索步驟如下。 (1)利用式(8)對Xi進行歸一化: i=1,2,…,N;j=1,2,…,D (8) 式中:Xjmax和Xjmin分別為可行域中第j維的最大值和最小值。 (2)生成混沌序列。隨機生成Z0,根據式(6)迭代生成M個混沌序列。 (9) (5)計算適應度值f(uij),并與Xi的適應度值f(Xi)進行比較,保留最好解。 1.2.2 自適應慣性權值 慣性權值是WOA算法中的一個重要參數,式(1)和式(5)中保持較大的慣性權值1,恒定不變的慣性權值將降低算法效率,不利于算法的全局尋優。Zhang等[12]指出較大的慣性權值有利于全局優化,較小的慣性權值有利于局部挖掘。基于此,提出一種基于適應度值的自適應慣性權值,以保證算法在迭代初期隨適應度值的不同而具有較大的非線性權值,在迭代后期具有較小的非線性權值策略。 在式(1)和式(5)中引入自適應慣性權值ω: (10) 式中:ffit(X)是個體X的適應度值;u為在第一次迭代計算中鯨魚種群中最佳的適應度值。 改進后的更新公式如下: X(t+1)= (11) 利用ω的動態非線性特性提高WOA算法的收斂精度和收斂速度。 ELM是一種新的單隱層前向神經網絡學習算法,與傳統神經網絡訓練學習的不同在于ELM隱層無需迭代,輸入權值和隱層節點偏置是隨機選擇設定的,以最小訓練誤差為目標,最終確定隱層輸出權值,該算法描述如下。 設m、M、n分別為網絡輸入層、隱層和輸出層的節點數,g(X)為隱層神經元的激活函數,bi為隱層閾值。n個樣本為(Xi,Y),其中Xi=[xi1,xi2,…,xim]T∈Rm,為網絡輸入向量,Y=[y1,y2,…,yj,…,yn]T∈Rn,為目標輸出向量。 ELM模型描述如下: (12) 式中:ωi=(ω1i,ω2i,…,ωmi),為連接網絡輸入層節點與第i個隱層節點的輸入權值向量;βi=[βi1,βi2,…,βin]T,為連接第i個隱層節點與網絡輸出層節點的輸出權值向量;O=[o1,o2,…,oj,…,on]T,為網絡輸出值。 ELM的代價函數E可表示為: (13) 式中:S=(ωi,bi),i=1,2,…,M,包含了網絡輸入權值及隱層閾值;β為輸出權值矩陣。 ELM的訓練目標是尋求最優S和β。min(E(S,β))可進一步描述為: (14) 式中:H為網絡關于樣本的隱層輸出矩陣。 其中, H(ω,b,X)= (15) (16) (17) 式中:H?為隱層輸出矩陣H的MP廣義逆。 ELM學習算法在回歸問題的計算性能和準確率等方面具有一定的優勢,在缺乏先驗知識情況下,ELM的輸入權值和隱層閾值通常隨機確定,并求出網絡的輸出權值。假如輸入權值和隱層閾值選擇不當,將會影響ELM的預測精度和泛化能力。針對該問題,采用CAWOA算法優化ELM模型,其核心思想是將樣本數據作為ELM模型的輸入,通過CAWOA算法搜索調整得到最佳輸入權值和隱層閾值,在隱層節點盡可能少的情況下使ELM算法的回歸效果最好,輸出權值矩陣β則通過解析MP廣義逆求得。圖1給出了CAWOA算法優化ELM模型參數的流程,具體步驟如下: (1)種群初始化。隨機產生由N個鯨魚個體組成的種群,鯨魚個體Xi按輸入權值和隱層閾值編碼,如Xi=(ω11,…,ω1m,…,ωM1,…,ωMm,b1,b2,…,bM)所示。 (2)變量選擇與數據采集。在進行NOx排放量預測建模時,選擇合理的輸入、輸出模式;并從燃燒系統采集、處理與建模相關的運行數據,將其分為訓練集和測試集。 (3)確定適應度函數J: (18) (4)模型選擇。根據初始種群建立NOx排放量預測模型并計算適應度值,如果適應度值不滿足要求,則采用CAWOA算法優化、選擇ELM的模型參數,直到得到滿意的結果為止,并建立CAWOA-ELM模型。 圖1 CAWOA算法優化ELM模型參數的流程 (5)模型驗證。利用測試集驗證CAWOA-ELM模型的性能。 鍋爐燃燒生成NOx的途徑主要有燃料型NOx、熱力型NOx和快速型NOx,其燃燒過程非常復雜,NOx的生成量與排放量受燃燒方式、燃燒器結構形式、運行風量、負荷和煤質特性等因素的影響,這些影響因素之間具有非線性、強耦合特性,常規的機理建模方法難以描述鍋爐燃燒過程。然而,NOx的精確計算是發電企業實現節能減排、環境保護的必要環節之一。ELM黑箱模型的出現為解決上述難題提供了一條有效途徑。 采用ELM建立鍋爐NOx排放量預測模型需要確立輸入、輸出參數。依據強相關性原則采用25個操作參數作為輸入參數,具體如下:鍋爐負荷;省煤器出口煙氣含氧體積分數;4個一次風速(v1、v2、v3和v4);4臺給煤機轉速,給煤機編號為A、B、C、D;二次風速,二次風共投入5層,同層聯動,各層編號為AA、AB、BC、CD、DE;燃盡風開度,燃盡風分別位于OFA上、OFA下、SOFA層;煤質特性w(Car)、w(Har)、w(Oar)、w(Nar)、w(Mt)、w(Aar)和發熱量Qar共7個參數用于描述煤質對NOx排放質量濃度的影響因素。預測NOx排放量的ELM簡化模型如圖2所示,選擇ELM模型的輸入節點數為25,輸出節點數為1,根據文獻[13]確定ELM模型的隱層節點數為8,構成25-8-1的ELM的NOx排放量預測模型。 圖2 鍋爐燃燒特性ELM簡化模型 以某330 MW煤粉鍋爐為研究對象,從其DCS系統中采集565組穩態運行樣本,如表1所示。在565組數據中,隨機選取550組穩態樣本訓練ELM模型,并建立基于CAWOA-ELM的NOx排放量預測模型;其余15組作為測試集,用來驗證模型的準確度和泛化能力。CAWOA-ELM模型對測試集的預測結果見圖3。為驗證CAWOA-ELM模型的性能,將其與粒子群算法(PSO)優化的ELM模型(PSO-ELM)、WOA-ELM和標準ELM 3種模型進行仿真對比,各方法預測誤差的絕對值見圖4。 從圖3可以看出,CAWOA-ELM模型的預測趨勢與真實值的趨勢相同,15個測試集雖存在一定估計誤差,但從熱工過程可接受誤差范圍來看,CAWOA-ELM模型能夠對測試集進行正確估計。 從圖4可以看出,ELM模型的預測誤差最大,說明隨機初始化輸入權值和隱層閾值的ELM模型預測精度不高;比較PSO-ELM、WOA-ELM與ELM模型曲線,前2種模型參數分別在PSO和WOA算法優化的情況下,其NOx排放質量濃度預測精度有明顯改善。從圖4還可以看出,CAWOA-ELM模型的預測誤差曲線最為平穩,且預測誤差最小,表明基于CAWOA-ELM模型的NOx排放質量濃度預測效果最好,同時也表明經過Sin混沌搜索策略和自適應慣性權值策略改進的CAWOA算法較WOA算法更能優化搜索到較好的輸入權值和隱層閾值。綜上所述,輸入權值和隱層閾值決定了ELM的泛化能力;CAWOA-ELM模型比PSO-ELM、WOA-ELM和ELM模型具有更優的泛化能力。 表1 鍋爐運行試驗數據 圖3 CAWOA-ELM模型對NOx排放質量濃度的預測結果 圖4 4種模型對NOx排放質量濃度的預測誤差 為了精確預測煤粉鍋爐NOx排放量,提出一種基于混沌自適應鯨魚優化算法與極限學習機結合的預測模型。采用CAWOA算法來預先選擇ELM模型參數以改善模型的預測精度和泛化能力。以某電廠330 MW煤粉鍋爐為測試對象,建立CAWOA-ELM的NOx排放量預測模型,通過DCS系統歷史運行穩態數據進行模型訓練,并利用穩態運行樣本對模型進行預測檢驗,仿真實例表明,CAWOA-ELM模型具有較好的準確性、較強的泛化能力和更高的實用價值。1.2 CAWOA算法
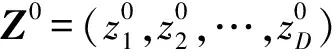
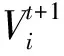
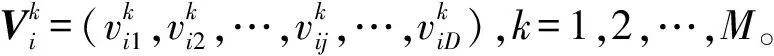
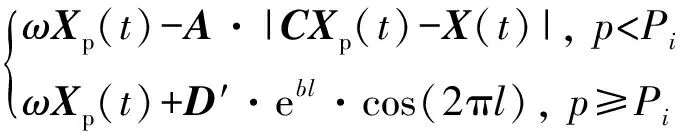
2 極限學習機模型
2.1 極限學習機基本原理
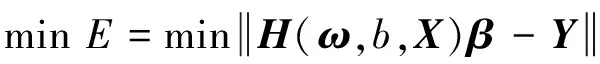
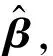
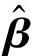
2.2 ELM模型
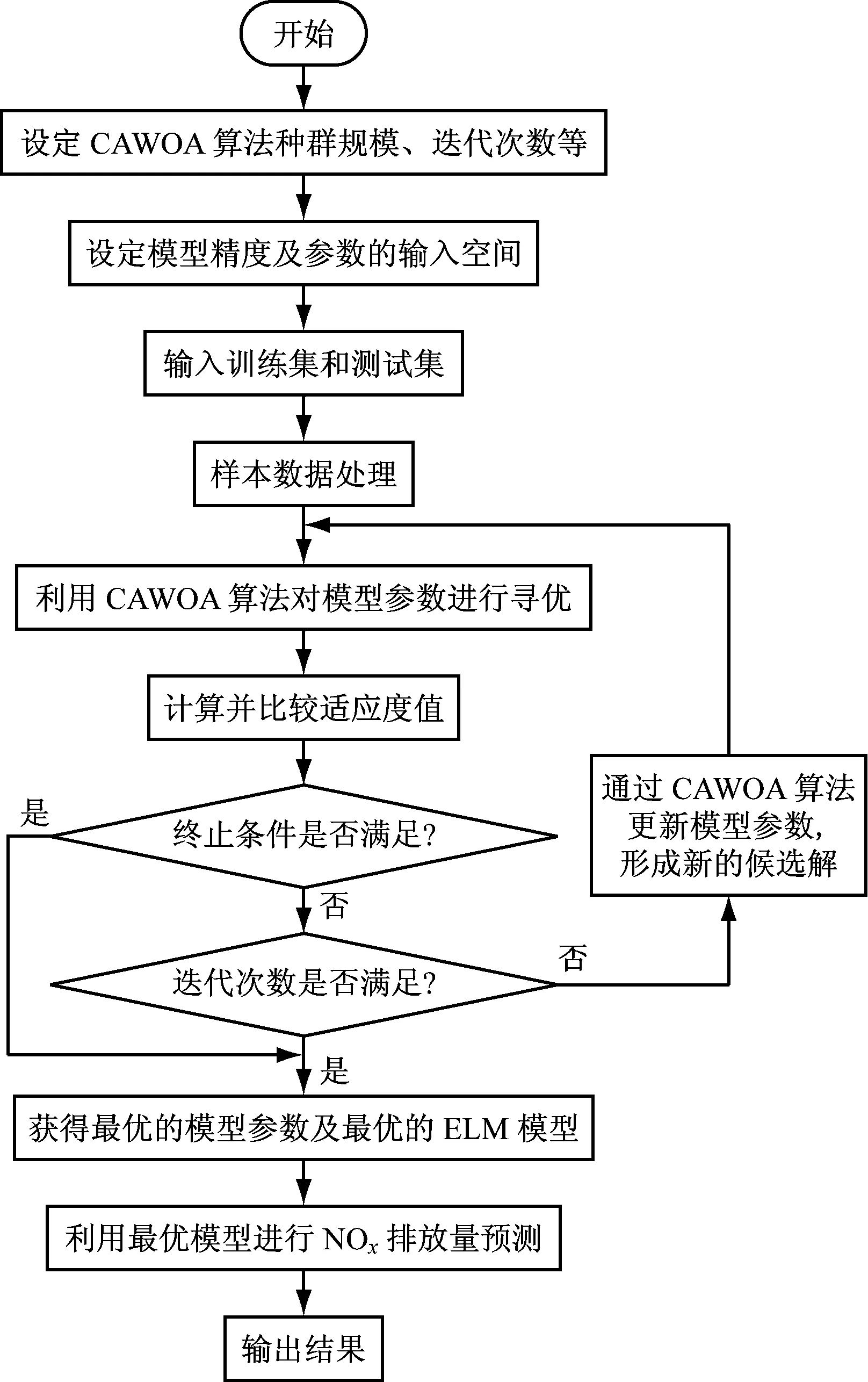
3 仿真實例
3.1 ELM模型的設計
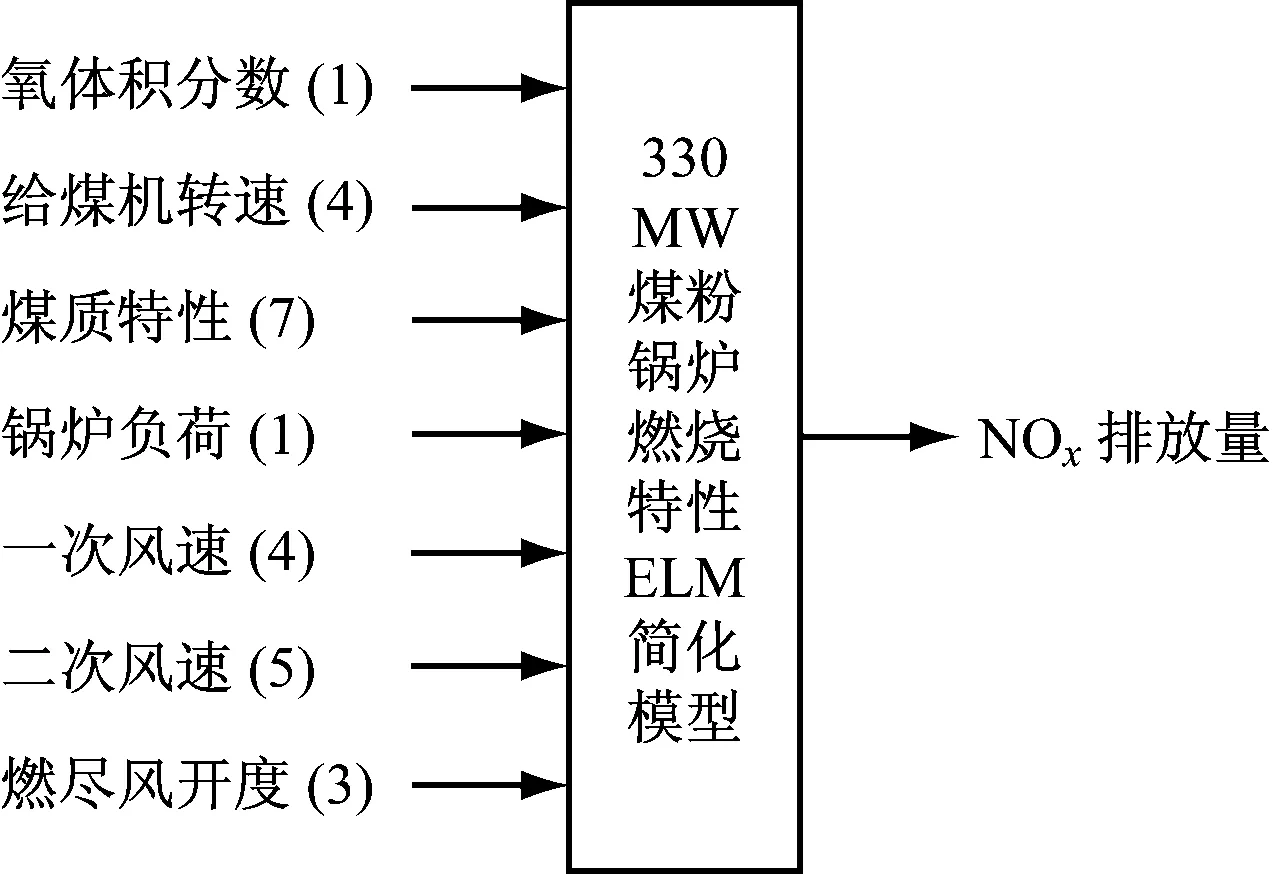
3.2 仿真實驗
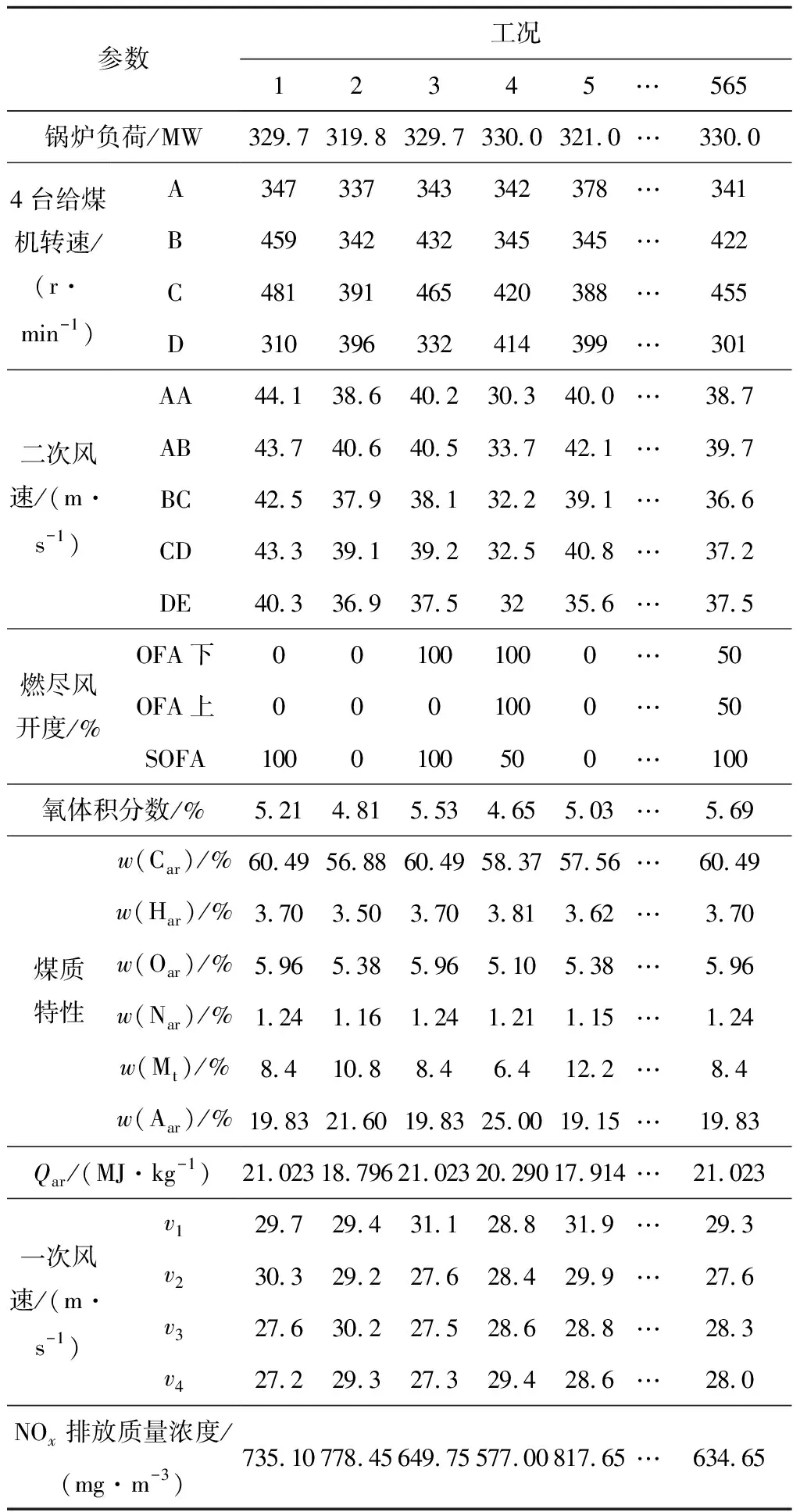
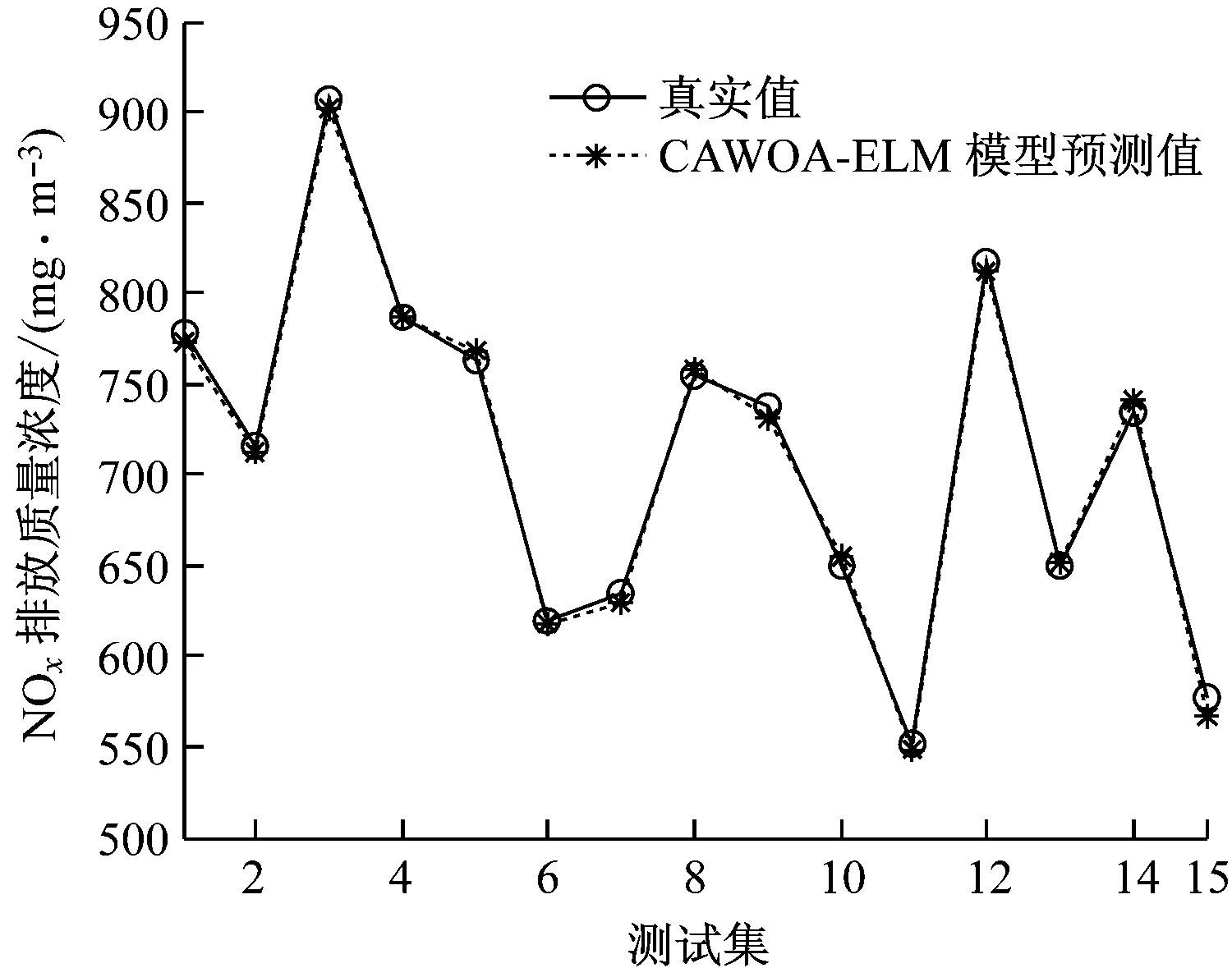
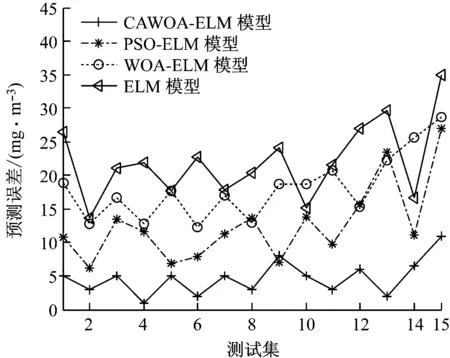
4 結 論

