例談高三解題教學中學生思維能力的培養

（宜昌市夷陵中學 湖北宜昌 430000）

數學教學是數學思維活動的教學，思維過程是數學教學的本質。美籍匈牙利數學家波利亞指出“掌握數學意味著善于解題”。在實施新課標理念和高考的雙重背景下，有效提高解題教學的質量，提升學生綜合能力及數學素養是廣大一線教師的不懈追求。解題教學的目的不僅僅是讓學生學會解題、善于解題、取得好成績，更重要的是培養學生的理性思維能力、數學素養，學會數學地思維，為學生的進一步發展奠定基礎。

高三解題教學包括例題教學和習題教學。前者常出現于一輪、二輪復習的典型例題分析中，以教師為主導，通過探中抽知、串知成鏈，引導學生利用學過的概念、公式、定理、法則等解決數學問題；后者常出現于作業題、試卷評講分析中，以學生為主體，充分暴露思維過程。在例題教學和習題教學中均可以通過一題多解、一題多變、多題一解等方式培養學生的思維能力。解題教學質量高低的關鍵是看學生的思維是否主動、積極、深度的參與解題教學活動。

一、高三解題教學首先要引導學生理解概念的本質

概念是數學思維的細胞，是構成數學知識體系的基本要素。對數學基本概念的理解是提高學生對數學的認識、提高數學思維能力的最好途徑。章建躍博士認為，概念及其蘊含的思想方法才是根本大法，只有圍繞數學概念的核心開展教學，在概念的本質和數學思想方法上給予點撥、講解，讓學生在理解概念及其所反應的數學思想和方法的基礎上，對細節問題、變化的問題進行深入思考，才能實現有效教學。

這道題得分的情況不甚理想，筆者所帶的是年級成績較好的班級，全班50人，出錯27人次。此題當時放在填空題第15題位置，除開極少數學生對此位置填空題的恐懼、不自信因素，更多是對數列的概念本質理解不夠透徹。

從后來的總結分析發現，絕大多數學生能理解題意，對任意的兩個正整數m,n(m≠n)都有(m-n)(am-an)＞0轉化為數列{an}在n∈N*上單調遞增。學生中有如下思路與結果：

思路一：y=(3-a)x-3在(-∞,7]上單調遞增，有3-a＞0，且y=ax-6在(7,+∞)上單調遞增，有a＞1，故1＜a＜3；

思路二：除了a＜3，還要注意端點處，即(3-a)7-3 ≤a，解得

正解：由題知1＜a＜3，由數列{an}在n∈N*上單調遞增有解得

思考：部分學生未理清題意，誤認為是分段函數f(x)在定義域上單調遞增；多數同學沒有弄清函數單調遞增與數列單調遞增的差異，以為數列單調遞增，其對應的函數也單調遞增，其轉化是不等價的。追根溯源，實則為學生對數列的概念沒有理清。數列其實是一種特殊的函數，我們可以用研究函數的方法來研究數列，回到數列的概念：按一定次序排成的一列數，通項公式為an=f(n)，定義域為N*或其子集，圖像是一系列孤立的散點。散點的變化規律與連續變化的曲線的變化規律既有聯系又有區別，本例思考的節點在于n=7和n=8時，數列{an}圖像中兩個點的比較。

思路一：

思路二：

思路三：

不妨設x1＞x2＞0，則等價于f(x1)-2x1＞f(x2)-2x2，令g(x)=f(x)-2x，有g(x1)＞g(x2)在(0,+∞ ) 上 恒成 立，即g(x)=f(x)-2x在(0,+∞)上單調遞增，則在(0,+∞)上恒成立，有a≥ 2x-x2在(0 ,+∞ )上恒成立，解得a≥1。（教師點撥，與學生共同完成）

點評：思路一近乎解答題的做法比較龐雜，不符合小題小做、小題巧做的規律，學生的想法值得肯定但思維的節點未合理突破；思路二的問題在于利用拉格朗日中值定理，其轉化是不等價的，且屬于高等數學范疇，不是通性通法；思路三立足高考考綱范圍內的知識點，利用單調性定義將問題轉化為函數在區間上單調遞增（減）的問題，由導數知識進一步轉化為恒成立問題。

二、高三解題教學中可以適時采用變式教學激活學生的思維

根據建構主義學習理論，學生是認知的主體，是認知結構的主動建構者，課堂教學中，教師只是認知結構建構過程的組織者、指導者、腳手架搭起者。解題教學也不例外，在解題教學中，教師通過精心設計一組有中心、有聯系、有層次、環環相扣的變式問題，給學生搭起輔助支架，以變式問題為主線，引導學生從不同角度，對不同問題開展探究活動，這對充分調動學生主動參與課堂活動的積極性，有效完成學生的知識建構，培養學生分析問題、解決問題的能力，拓展學生的思維，提升學生的綜合素養是有益的。

思考：愛因斯坦說“提出問題比解決問題更重要”。教師通過創設民主課堂，建立積極和諧的師生關系，鼓勵學生自行設計題目，充分體現學生的主體地位，極大程度地調動了學生學習的積極性，激發了學生的創造性思維及學習潛能，鍛煉了學生“如何數學地提出問題并分析問題”的能力。在這種開放的教學環境中，學生主動性得以加強，思維能力得以提升，教師的“無為”造就了學生的“有為”。

但在設計題目的活動中，對學生天馬行空的設計教師需要把握一個合適的度，在肯定學生積極主動思考問題的同時又必須緊扣本節課的教學目標，所以教師需要及時對學生設計的問題進行適當點評與修改。

筆者隨后補充了如下題目：

1.已知直線過點P(2,1)，且在坐標軸上的截距相等，求直線方程；

2.已知直線過點P(2,1)，且與坐標軸圍成的面積為8，求直線方程；

3.已知直線過點P(2,1)，且與x軸、y軸正半軸分別交于A、B兩點，思考△AOB的面積是否存在最值，并研究當面積取得最值時直線的方程。

并與學生共同探究第3題，學生給出了這樣的思路與解法：

生8：△AOB的面積不可能有最大值，但有最小值。考慮到△AOB為直角三角形，可以考慮設直線方程的截距式依題有利用基本不等式得到ab≥8，當且僅當a=4 ,b=2 時有面積的最小值4，此時直線方程為x+2y-4=0；

教師：哪位同學能點評一下這兩種方法么？

生10：法一用兩個變量a,b很簡潔地表示了面積，法二只用了一個變量k來表示面積，兩種方法均用到了基本不等式；

教師：點評得很好。方法二將面積S表示成了關于k的一個……？

學生：函數；

教師：方法一能否利用函數的觀點來研究？

教師：我們還能選擇其他的變量來表示面積么？

生12：可設 ∠PAO=α，利用三角函數的知識來刻畫面積S，當且僅當時，有Smin=4，此時對應直線的斜率為方程為x+2y-4= 0 ；

生13：他的方法很不錯，中間我們還可以使用柯西不等式來求最值，即當且僅當時，有Smin=4筆者隨后給出了如下變式題：

變式一、設直線l與x軸、y軸正半軸分別交于A、B兩點，且直線l與單位圓相切于點P，求△AOB的面積S的最小值。

學生思考片刻后，筆者鼓勵完成解題的學生在黑板上寫出解答過程與大家共同分享，結果先后共有13位學生上臺書寫解答，最后筆者與學生共同梳理、比較、提煉，摘錄如下：

法一：設直線Ax+By+C=0，

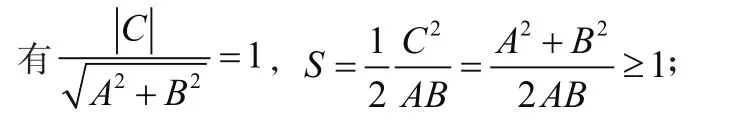
變式二、已知直線過點P(2,1)，且與x軸、y軸正半軸分別交于A、B兩點，求的最值。（或變為求PA·PB的最值）

變式三、已知直線過點P(2,1)，且與x軸、y軸正半軸分別交于A、B兩點，求OA+OB的最小值。

變式四、已知直線過點P(2,1)，且與x軸、y軸正半軸分別交于A、B兩點，求OA2+OB2的最小值。

變式五、已知直線過點P(2,1)，且與x軸、y軸正半軸分別交于A、B兩點，求△AOB的周長的最小值。

思考：在解題教學中，教師可在學生的最近思維發展區內設計問題，可嘗試對來源于課本的習題進行改編，設計能引起學生積極思維的問題，讓學生能“跳一跳夠得著”，通過一題多解、一題多變進行不同方面、不同角度、不同層次的分析和探索，進而提高課堂效率，讓學生在思考探究的過程中尋求各種解題途徑，激發學習興趣，使學生體驗到成功的喜悅、增強自信心，也很好地培養了思維能力。同時注意解后對多種解法進行反思、評價、提煉，深入推進學生的思維活動，從而更好地提高思維層次。

三、在解題教學中引導學生養成解后反思的好習慣

波利亞在《怎樣解題》中把解題過程概括為四個環節：審題——探究——表達——反思。但在很多師生的眼里，認為解題就是前面的三個環節：認真審題讀懂題意，在大腦中檢索、聯想并設計解題思路，嚴謹規范地寫出解答過程。尤其是學生，他們解題的興奮點大多在結果上，一旦解出正確結果，喜上眉梢，如釋重負，卻忽視了解后的反思。

案例三、已知函數f(x)= s in3x+ 2 015x， 對任意的m∈[- 2 ,2]，都有不等式f(mx- 2 )+f(x)＜ 0 恒成立，則x的取值范圍是________________

反思知識點：單調性、奇偶性、導數、“一次”不等式恒成立；

反思易錯點：關于m的“一次”不等式恒成立問題；

反思解題的實質：想辦法“脫去”對應法則f這件“外衣”；反思用同樣的方法做過的題目（學生舉例說明）

2.設f(x)是定義在R上的奇函數，且當x≥0時，f(x)=x2，若對任意的x∈[t,t+2 ]，不等式f(x+t) ≥ 2f(x)恒成立，則實數t的取值范圍是

筆者隨后給出如下習題，讓學生思考與原題的區別：

實質：本題是“穿上”對應法則f這件“外衣”。

在解題教學中，教師可以從以下幾個方面引導學生進行反思：解決問題的關鍵是什么？如何進行突破？還有其他的解法嗎？解決這類問題的最佳方法是什么？這種思路為什么行不通？本題能否進行變式、推廣和延伸？

問題是數學的起點，解是問題的終點，數學思維活動是連接問題和解題的紐帶和橋梁。在解題教學中，在注重夯實基礎的前提下，倡導理性思維、強化探究變式與拓展，變教師的主講為主導、變教師的精辟分析為學生的思索感悟，要能夠充分放手讓學生參與自主探究、合作交流活動，使學生在成功與失敗、正確與錯誤的矛盾沖突中層層深入，激起學生思維碰撞的火花。