化歸思想在高中數學解題中的應用探析

（福建省莆田第六中學 福建莆田 351100）

一、化歸思想在高中數學解題中的意義

化歸思想的實質就是以運動變化發展的觀點，以及事物之間相互聯系相互制約的觀點看待問題，善于對所要解決的問題進行變換轉化，使問題得以解決，其思維模式為“將原問題轉化為新問題，通過解決新問題來化解原問題”。化歸思想在高中數學解題中占據重要地位，其意義主要表現在：

1.化歸思想是構建數學解題思路的基礎。從數學思想及解題方法來看，化歸思想是核心。如數形結合思想就是將“數量”與“形狀”進行相互轉換；函數與方程思想就是通過函數與方程、函數與不等式相互轉換來解決問題；分類討論思想就是將整體劃分為多個部分來化解全局性問題。

2.化歸思想在解題應用中具有廣泛性。在高中數學，知識的呈現多遵循由淺入深的過程，在教學中也是根據舊知識來滲透新知識，化歸思想的學習和應用，順應學生由已知向未知的學習需求，符合學生的思維習慣，便于提升學生數學素養。

3.化歸思想在解題思路上易于被學生接受。高中生已經具備相應的數學知識儲備，利用化歸思想，可以加深對數學問題的分析，銜接理論知識與實際應用，提升學生解決數學問題的能力。

二、化歸思想在高中數學解題中的應用

化歸作為一種思想方法，應包括化歸的對象、化歸的目標、以及化歸的方法、途徑三個要素。化歸思想的實施應有明確的對象、設計好目標、選擇好方法。

1.化歸思想在函數中的應用

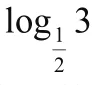
2所對應函數值的大小。首先分析函數的單調性，根據對數函數的基本特征，函數y= l og1x為減函數，也就是說y隨著x值的增

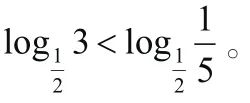
2.化歸思想在不等式中的應用

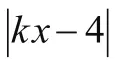
3.化歸思想在數列中的應用

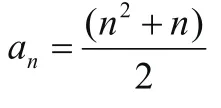
結語

利用化歸思想解題時，轉化的途徑和方法不一定相同，但有一個共同的規律，就是在待解決的問題和已解問題之間架起一個聯系的橋梁，要領悟蘊含在數學內容之中的數學思想方法，這些都是提高數學解題能力和數學核心素養的條件和基礎。