應用Copula函數的潘家口水庫設計洪水線推求

喀迪爾·麥麥提

（新疆英吉沙縣水利局，新疆 英吉沙 844500）

0 引言

洪水過程線隨機模擬是水利工程防洪設計的關鍵內容，也是水利安全、洪水災害控制的依據[1]。此前防洪設計中以傳統單變量倍比放大或同頻率設計方案為主，雖然其操作流程簡易、各特征量重現周期易于滿足防洪標準，但仍需要指出的是存在明顯局限性：①單純考慮洪水特征量，忽視了期間非線性、相關性關系[2]；②將防洪安全標準與設計洪水過程線的特征量的頻率等同考慮，避開了洪水過程聯動性等水文規律[3]。隨著計算科學的發展，國內外學者提出了自回歸[4]、多元統計[5]、典型解集模型[6]、神經網絡[7]等模型應用于洪水過程隨機模擬，然而未能有效識別變量間共線性、依存關系，且難以實現多維變量聯合分布分析。Copula函數能夠聯立多變量間復雜關系，其邊緣分布靈活多樣，在水文研究中取得良好應用。高超等[8]運用用三維Copula函數以構建洪水特征量聯合分布模型，并探究了洪水過程線形狀和三維對稱型Archimedean Copula函數公式對模擬精度的影響；劉和昌等[9]構建了基于Copula函數的洪峰、洪量之間的函數關系，由此計算了峰量的邊緣分布頻率；李天元等[10]以隔延河水庫為例，對比分析了單變量同頻與多變量同頻洪水過程線設計的差異，結果表明，基于Copula函數構造的聯合分布模型由于傳統同倍比方法。鑒于此，本文以二維Copula函數為基礎理論建立潘家口水庫峰量的聯合分布，并推求設計洪水，以期為水庫安全管理提供基礎信息。

1 原理與方法

1.1 Copula函數原理

Copula函數是基于多元分布理論而將聯合分布函數與邊緣分布函數連接構建的一種相依性測度方法，對于傳統共線性問題不能準確識別變量間相依信息，Copula能夠排除這些高度相關影響，以構造二維離散分布模型進行隨機模擬。Nelsen[11]將N元Copula函數定義域設定為[0～1]；其在洪水過程線模擬的應用通常以1、2、3維度為主，本研究采樣雙變量同頻率設計方案，故針對二維Copula函數表達如下[12]：

式中：C 為 Copula 函數，U1(x1)，U2(x2)，…，Un(xn)在區間是連續分布的；則其相應的聯合概率密度函數表示如下：

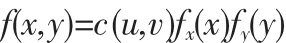
式中：u=FX(x),v=FY(x)分別代表分別為隨機變量X、Y的邊緣分布函數。洪水過程是洪峰、時段等特征量的函數，具有多元、非線性特征，因而二維變量聯合分布模擬多以Archimedean Copula函數函數簇應用較多，且適應性強，其能夠糾正共線性情形，辨識上尾相關性，其公式如下：

式中：u、v、r均為邊際分布函數，θ為Copula函數的參數。其密度函數為：

函數參數θ與Kendall秩相關系數τ關系表示如下：

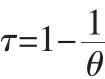
1.2 邊緣分布頻率

洪峰、洪量是洪水過程的矢量之一，其隨時間變化符合PIII分布。已知洪峰Q、洪量W的分布函數為[13]：

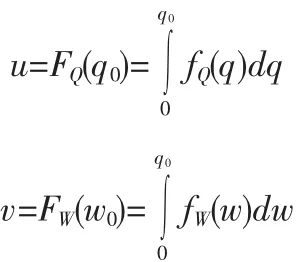
式中：q0、w0分別表示洪峰、時段洪量給定值；a、β、a0依次為形狀、尺度、位置參數，其用于度量洪水特征。根據邊緣分布概率定理；則其二維離散型頻率計算公式如下：

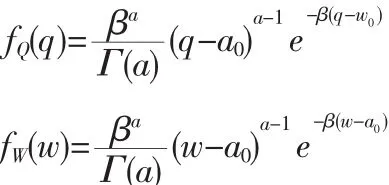
式中：T為伽馬函數。

1.3 推求設計洪水過程線

以洪峰、洪量、洪水歷時等特征量構建Copula聯合分布函數進行聯合模擬，以描述洪水過程。基于Copula函數，在指定洪水歷時條件下，其分布如下[14]：

上式可轉化為：

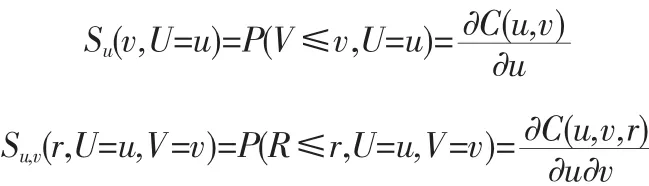
假設Copula函數具有三變量重現期u、v、r，則在區間上存在無數個連續的u、v、r組合，然而實際洪水過程具有一定歷時，因此其組合個數的有限、可知的。遵循同頻倍比法，當洪峰與時段洪量同頻時，即可滿足u=v=r條件，則洪水過程線聯合重現期可通過頻率組合C(u，v，r)來描述。基于此，可先運用邊緣分布P-III函數推求洪峰與時段洪量的聯合設計值組合，在此基礎上進行同倍比方法洪水過程，從而得到多遍了聯合分布模擬結果。

2 實例分析

2.1 潘家口水庫庫區概況

潘家口水庫位于灤河上游、唐山市燕山南麓，控制徑流面積8540 km2，是華北地區重要水利工程之一。庫區位于燕山迎風坡降水中心地帶，年平均降水量介于400 mm～700 mm；區域水系發育充分、年內分配不均，特別是7月～8月降水占全年降水的60%，為洪水多發季節。據多年暴雨資料測算顯示，區域洪水過程達3 d～4 d，洪峰歷時約30 h，落水在40 h～50 h之間，洪量占全年徑流量的20%～40%，洪水年際差異大。監測期內(1929年～2015年)最大洪峰流量出現在1962年，洪峰流量達18800 m3/s，最大六日洪量18.53億m3；1958年7月洪峰流量達9570 m3/s，最大六日洪量為16.52億m3；最近的一次洪水發生在2012年，洪峰流量達4280m3/s，相應水位為226.69 m

2.2 潘家口水庫設計洪水參數選定

潘家口水庫兼具防洪、灌溉、飲水、養殖等多元功能，然而其設計初衷在于防患水患。其依據灤縣站、欒南站的1929年～1970年間42年序列監測數據，并參考了1938年、1949年、1958年、1959年、1962年、1964年等年份的洪水資料。鑒于該項目的二期工程實施，本文將實測系列延伸至2015年；以3d、6d為基準時段，運用最大取樣法計算其設計流量，并以《潘家口水庫調度方式研究報告》為依據進行復核，其設計結果見表1。計算了各項參數設計值與復核值之間的絕對誤差，結果表明其誤差介于0.8%～3.2%之間，說明設計洪水參數穩定、可靠；另外各參數均值大部分略有偏小，只有極個別偏大，表明原設計成果相對保守、安全，基于多年來汛情特征和設計經驗，故仍以最初設計值為選定標準。

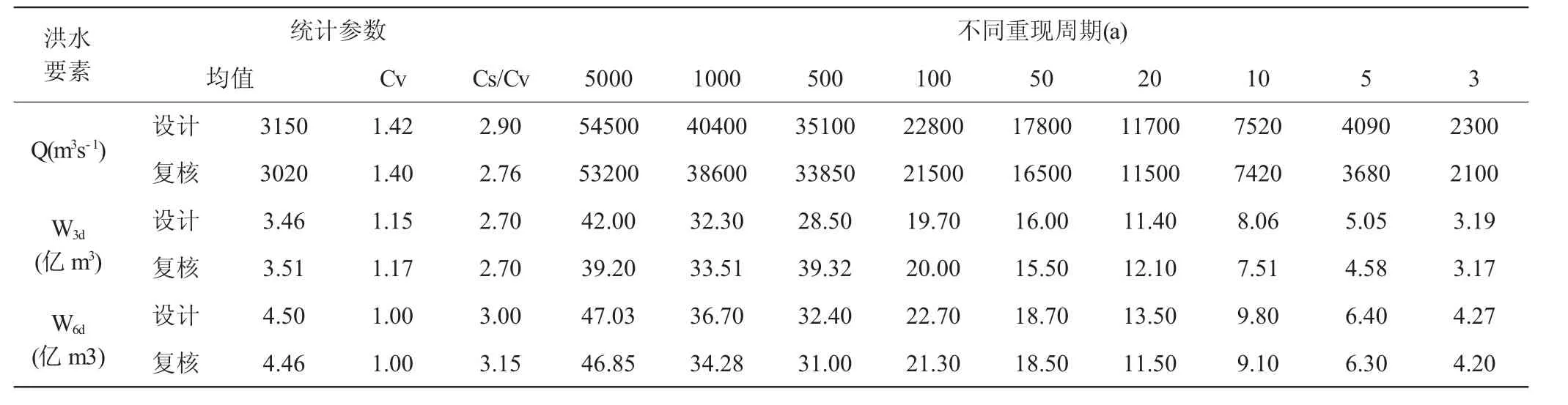
表1 潘家口水庫年最大設計洪水成果

2.3 基于Copula模型的洪峰流量聯合分布

洪水事件是典型的自然概率問題，最大似然估計可以精確求算一個樣本集的相關概率密度，因而被廣泛應用于平穩、非平穩自然變量聯合分布研究中。鑒于此，參照文獻[11-12]中的方案，先應用Gumbel-Hougaard Copula二維離散函數構建3 d、6 d洪量的聯合分布模型，根據經驗頻率公式p=m(i)/(n+1)計算，并滿足n個樣本容量中有m(i)個聯合觀測樣本子集服從 x≤xi且 y≤yi；得到其 kendall秩相關系數 τ分別為0.6321、0.5963；然后運用非對稱 Gumbel-Hougaard Copula函數建立3 d、6 d洪量的三維聯合分布模型，基于最大似然法得到參數θ分別為0.2712、0.2518；雖然潘家口水庫上游建立了2個水庫工程，但其為微小型水庫、控制面積和庫容量均較小，因而可忽略其影響。潘家口水庫年最大洪峰與96 h洪量的邊緣分布(P-Ⅲ)頻率曲線見圖1，為便于直觀表達，統一采用升序排列；依圖可知其邊緣分布頻率符合指數模型 (yW=1760.9e-0.038x，R2=0.9966；yQ= 89.116e-0.038x，R2=0.9966)，擬合良好、精度可靠。

圖1 潘家口水庫年最大洪峰與96 h洪量頻率曲線

高超等[12]在類似于潘家口水庫群的設計洪水過程線研究中分別比較了 Clayton Copula、Gumbel Copula、Frank Copula 等三種函數對洪水特征量模擬效果的差異，多站數據均顯示以Frank Copula函數模擬精度最佳，基于此本文采用該函數計算潘家口水庫三變量間的理論聯合概率。圖2-a、2-b、2-c為依次為潘家口水庫的灤縣站、灤南站和二站綜合平均值的最大洪峰與96 h的洪量頻率分布曲線。從圖中可看出，各站和綜合評價資料的得出的洪水特征量的理論概率點和經驗概率值均密集分布于y=x直線附近，擬合函數為 (y=1.0043x+0.5142，R2=0.9966；y=1.0163x+0.3251，R2=0.998；y=1.0109x-0.9308，R2=0.9967)，均通過5%水平信度檢驗，說明擬合結果較好，該模擬結果合理、可信。

圖2 潘家口年最大洪峰流量與168h 洪量的理論頻率與經驗頻率擬合圖

2.4 潘家口水庫協防調度規則

潘家口水庫目前執行的是壩前各級控制水位與限制下泄流量相結合的調度方法，即當洪水入庫時，以庫水位是否超過某一控制水位來判別洪水達到哪一級標準，在每一級控制水位之下則按相應的防洪標準執行某級限泄流量。潘家口水庫現狀洪水調度方式實施兩級控泄。具體調度原則為：

①上游入庫洪水達到50年一遇及以下標準洪水控泄10000 m3/s，保京山鐵路大橋安全。

②50年～500年一遇洪水控泄28000 m3/s，保潘家口電站安全。

③大于500年一遇洪水不控泄。

2.5 推求設計洪水過程線

在對潘家口水庫進行補測時應用階段用暴雨移置法、水汽入流指標法及暴雨組合法，以1962年作為洪水典型年，設定聯合重現周期為1000a，另補充了50a的周期；于洪峰、洪量等值區間內等距抽取200組設計值子集，經通倍比放大后按照防洪調度規律演算其汛限水位，得到其限值依次為Zmax=229.6 m、Zmin=231.5 m，這一結果于1976年以來沿用至今。基于表1中給出的潘家口洪水特征量設計值(Q=40400 m3/s，W6h=36.7億m3)，經同頻率放大推算了1955年設計洪水過程線，見圖3、表2。

可知，對1995年典型洪水過程推求，以單變量同頻率計算得到其最高水位為231.58 m，而雙變量同頻率得到其最高水位為231.69 m，這一結果表明兩種設計方法對汛限調度來講比較合理；但從防洪角度來看，單變量同頻設計相當保守，不利于極端天氣條件下調洪協防。

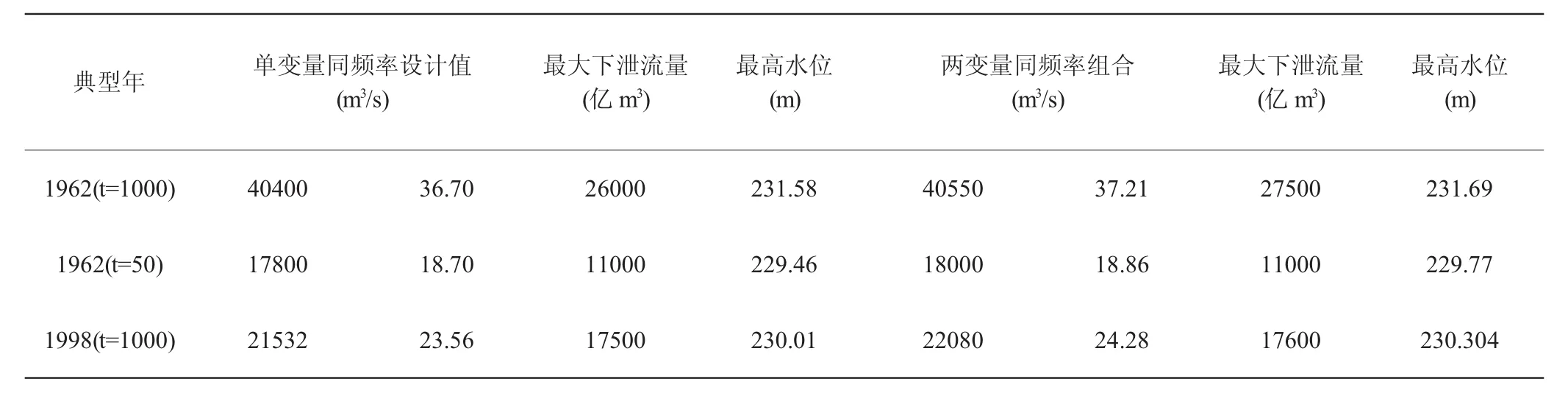
表2 潘家口水庫千年一遇設計洪水調洪結果

鑒于1998年該流域發生特大洪水事件，另以該年為典型年，應用雙變量同頻率并推求其洪水過程線，以驗證該設計的合理性，結果見表2、圖4。由圖4可知1998年典型年潘家口水庫洪水過程歷時時間長，最高洪峰流量高達21532 m3s-1，最高水位達230.304 m，洪峰歷時約30 h；入庫與出庫流量近似同步但略有滯后。由表2可知，1962年和1988年典型年中采用雙變量同頻設計的潘家口洪水特征參數值略高于單變量同頻設計方法，因此前者更利于庫區防洪；另外以雙變量的聯合重現期作為防洪標準，更符合洪水過程規律，因此該方案具有科學、合理性。

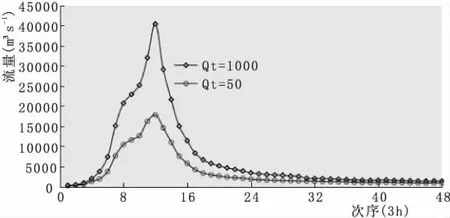
圖3 潘家口水庫千年、五十年一遇設計洪水過程線比較(1962典型年)

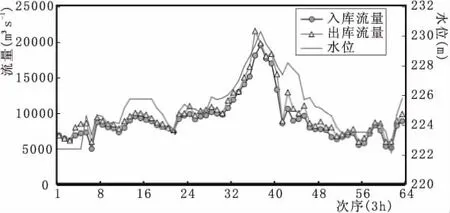
圖4 兩變量同頻率組合下潘家口水庫千年一遇設計洪水調洪過程線(1998年典型)

3 結論

區別于傳統單變量同頻設計洪水過程線獨立控制洪水各特征量重現周期，未能針對整個洪水過程聯合分布進行模擬，本文利用Copula函數構造了基于長時歷史洪水資料的洪水特征量多變量聯合分布模型，該方案更符合防洪安全標準，適用于水文工程實際應用。

洪水過程具有隨機非線性、多元化特征，Copula函數隨機模擬考慮了洪水特征量直接復雜相依關系。基于雙變量同頻率分析，經水庫調洪演算后得到洪水歷時洪峰、洪量、最高水位，從而得到潘家口水庫洪水過程線。相較于單變量同頻模擬而言，以雙變量同頻推求的最高水位限值略大，并介于上下限制區間內；由此可知，基于防洪安全角度，采用雙變量同頻組合設計能夠更好適應于氣候變化背景下極端天氣引起的洪水不確定性。