鑄造奧氏體不銹鋼中鐵素體與奧氏體位向關系及其對聲衰減的影響?

羅忠兵 董慧君 馬志遠 鄒龍江 朱效磊 林莉

(大連理工大學無損檢測研究所,大連 116085)

(2018年6月28日收到;2018年9月18日收到修改稿)

1 引 言

鑄造奧氏體不銹鋼(cast austenitic stainless steel,CASS)廣泛用于石油化工、核電等領域關鍵構件.以Z3CN20-09M鋼為例,主要用于壓水堆核電站一回路主管道,具有奧氏體、鐵素體兩相組織,RCC-M 規定鐵素體體積分數為12%—20%,并有助于提高抗熱裂紋、抗腐蝕和焊接性能,綜合力學性能優異[1?4].由于構件多長期服役于高溫、高壓等惡劣環境,易發生力學損傷.鑄造過程中產生的微小缺陷也可作為裂紋源,促進裂紋的形核和擴展.因此,鑄造奧氏體不銹鋼中微小缺陷和損傷的有效檢測對保障關鍵構件的安全運行十分重要.

基于超聲方法的材料微觀組織、結構、性能評價已經被大量研究報道[5?7].由于鑄造奧氏體不銹鋼構件尺寸較大(核電主管道壁厚66—110 mm)、鑄造冷速較低、奧氏體晶粒粗大、彈性各向異性明顯,給基于聲學方法的微小缺陷和損傷檢測帶來了困難.美國西北太平洋國家實驗室的研究結果表明[8]:為降低彈性各向異性奧氏體導致的結構噪聲,提高檢測信噪比,超聲檢測頻率一般為0.5—2.0 MHz,此時鐵素體尺寸與超聲波長相比較小,聲散射效應通常被忽略,只需考慮奧氏體晶粒.類似處理在Sakamoto等[9]和Chen等[10,11]的研究工作中也得到體現.然而,對于表面或亞表面亞毫米甚至更小的缺陷和損傷,必須提高超聲檢測頻率,一般均在10 MHz以上[12],個別研究竟高達100 MHz[13].按10 MHz計算,對應超聲波長約0.6 mm,與鐵素體晶粒尺寸同一量級.此時,鐵素體如何影響超聲波傳播行為和檢測評價結果是很多研究面臨的棘手問題,目前尚無定論[14,15].Inoue和Koseki[16]研究表明,離心鑄造非平衡凝固過程中,晶體生長行為受到影響,鐵素體晶粒形貌及其與奧氏體兩相界面都具有一定特殊性,從而影響材料變形過程中微觀損傷發展規律,也會影響異質界面聲阻抗和超聲波的傳播行為[9].因此,研究CASS中鐵素體與奧氏體的位向關系,厘清聲衰減的影響因素及規律對于提高微小缺陷和損傷評價質量非常關鍵.

本文以Z3CN20-09M鑄造奧氏體不銹鋼為對象,基于鐵素體與奧氏體之間的位向關系分析,借助聲學仿真與“原位”實驗設計,通過模型材料分析了聲衰減系數的影響因素及其規律,為闡明CASS聲學響應機制和發展定量評價方法提供支撐.

2 實 驗

Z3CN20-09M鑄造奧氏體不銹鋼試樣取自壓水堆核電站一回路主管道余料,主要成分為(質量分數,%):Fe 68.142,C 0.027,S 0.014,Si 1.27,Mn 1.13,P 0.023,Cr 20.09,Ni 8.92,Mo 0.21,Cu 0.094,Co 0.044,N 0.032,B 0.004.如圖1(a)所示,從內徑800 mm、壁厚80 mm的管道上切取80 mm厚的試塊,垂直于管道軸向方向對試樣打磨拋光,分別用高氯酸或草酸溶液對試樣進行腐蝕,獲取樣品沿壁厚方向上的宏微觀組織,并利用Leica MEF-3型光學顯微鏡和Olympus OLS-4000型激光共聚焦顯微鏡進行觀察.確定管道柱狀晶和等軸晶位置后,垂直于柱狀晶生長方向制備板狀試樣,厚度約1 mm.借助Buller Vibrome-2型自動振動拋光儀制備試樣,用于電子背散射衍射(electron back-scatter dif f raction,EBSD)分析奧氏體、鐵素體取向及其位向關系.所用儀器為Zeiss Supra 55型場發射掃描電鏡(scanning electron microscope,SEM)和Oxford EBSD分析儀.考慮測試精度和效率的平衡,利用EBSD獲得等軸晶和柱狀晶表面分布時步長選用10μm,在進行兩相位向關系分析時,鐵素體不可忽略,步長選用1μm.

利用三軸水浸超聲C掃描系統和超聲脈沖回波法垂直于試樣表面采集A掃描信號,步進采樣間隔0.1 mm,重復定位精度6±0.02 mm.所用探頭為Olympus水浸聚焦探頭,入射頻率為15 MHz.根據一次底面回波與二次底面回波時間差值及幅值計算相應縱波聲速和聲衰減系數.

圖1 Z3CN20-09M鋼試樣及其組織 (a)取樣示意圖(單位:mm);(b)宏觀組織Fig.1 .Specimen and macrostructure of Z3CN20-09M:(a) sampling(unit:mm);(b)macrostructure.

3 結果與討論

3.1CASS的組織結構

CASS宏觀組織如圖1(b)所示.奧氏體晶粒粗大且不均勻,管道外壁為柱狀晶,長度可達十幾毫米,其余部分為等軸晶,沿壁厚方向晶粒大小并不均勻,直徑在1—5 mm,以內壁晶粒最為粗大.利用EBSD分析試樣表面法向的晶體取向,分別獲得等軸晶和柱狀晶晶粒取向分布圖,如圖2所示.可以看出,等軸晶區的奧氏體晶體取向呈隨機分布,晶粒大小并不均勻,形狀多不規則,長條狀和等軸狀均有發現;柱狀晶區奧氏體晶粒卻有明顯不同,具有明顯的方向性,即擇優取向,以〈101〉方向為主,個別位置也有少量近〈001〉方向晶粒.從兩者取向分布圖也可以看出,較大晶粒取向分布圖內部顏色并不均勻,存在多個取向微區,說明凝固過程中晶體生長受到了較大影響.已有研究表明:CASS粗晶結構彈性各向異性顯著,材料的聲學特性與傳播方向即奧氏體的晶體取向關系密切[9,17,18].

為方便后續的聲學建模和實驗驗證,選取圖2(b)中同為〈101〉取向的柱狀奧氏體晶粒,利用激光共聚焦顯微鏡得到兩種典型的鐵素體晶粒形貌,如圖3所示,兩者分別呈長條狀(圖3(a))和島狀(圖3(b)).對其形貌特征進行定量統計,前者鐵素體晶粒平均長度為(189±108)μm,后者僅為(57±49)μm,差異顯著.鐵素體總含量約為15%,這樣的微觀組織保證了鑄造奧氏體不銹鋼的綜合力學性能,也有助于提高耐晶間腐蝕能力[19,20].進一步借助EBSD進行微區分析,發現兩處鐵素體晶體取向一致,為〈106〉,即除鐵素體形貌不同外,兩典型位置的奧氏體、鐵素體晶體取向均相同,且這兩處奧氏體與鐵素體之間滿足Kurdjumov-Sachs(K-S)關系,這就為后續的實驗測試提供了理想的模型材料.

圖2 Z3CN20-09M鋼晶體取向分布圖 (a)等軸晶區;(b)柱狀晶區Fig.2 .Crystal orientation prof i le of Z3CN20-09:(a)Equiaxed crystal;(b)columnar crystal.

圖3 鐵素體晶粒典型形貌和晶粒取向 (a)位置1,條狀為主;(b)位置2,島狀為主Fig.3 .Typical morphology and crystal orientation of ferrite grains:(a)Position 1,mainly bar;(b)position 2,mainly island.

3.2 鐵素體與奧氏體位向關系

兩相的位向關系決定了兩相的適配程度,直接影響界面聲阻抗等關鍵聲學參量,從而影響超聲波的傳播行為.基于EBSD極圖方法進行取向關系鑒定時,不需要知道兩相信息,僅需確定不同米勒指數上的極圖分布,可以在較大范圍內分析相間晶體學特征[21].這里對CASS等軸晶和柱狀晶區奧氏體和鐵素體兩相取向關系進行了分析,典型情況如圖4和圖5所示.

以等軸晶為例加以說明.根據圖4(a)等軸晶表面法向取向分布圖,進一步分析獲取奧氏體相{111}面的極圖與鐵素體相{110}面的極圖,兩者疊加后如圖4(b)所示,紅色圓圈所示位置代表奧氏體和鐵素體相的極射投影完全重合,即奧氏體{111}面與鐵素體{100}面平行({111}γ//{110}α),表明奧氏體與鐵素體的取向關系為K-S關系或者Nishiyama-Wassermann(N-W)關系.同樣獲取奧氏體相〈110〉方向、〈112〉方向和鐵素體相〈111〉方向的極圖,發現奧氏體〈110〉方向和鐵素體〈111〉方向重合(如圖4(c)),滿足平行關系,但奧氏體〈112〉方向和鐵素體〈111〉方向極圖中沒有重疊位置,即{111}γ//{110}α,〈110〉γ//〈111〉α,因此滿足K-S關系.這與多數研究得到的結論相同[22?24].同時,研究中也發現一些例外,如圖5(a)中奧氏體等軸晶中分布有條狀鐵素體,{111}γ//{110}α(圖5(b)), 但 〈110〉γ方向和 〈111〉α方向并不重合,而是〈112〉γ//〈110〉α(圖5(c)),因此滿足N-W關系.多處分析結果均證實:CASS中無論等軸晶還是柱狀晶,兩相均以K-S關系為主,少量滿足N-W關系.

晶粒學中有四種典型的取向關系,分別為Brain關系,K-S關系,N-W關系和Greninger-Troiano關系[25].從鐵碳二元相圖可以看出,CASS平衡凝固過程中,δ-鐵素體首先在液相中形成,隨著溫度的降低,奧氏體晶粒在鐵素體中經包晶反應形成[24].Brooks和Thompson[26]認為,由于鑄造凝固過程中冷卻速率較高,導致高溫δ-鐵素體來不及轉化為奧氏體相,以多種形態保留到鑄坯中,而轉化后的奧氏體相則在母相鐵素體特定晶面上形成,在切變過程中兩相滿足K-S關系.同時由于離心鑄造等原因,晶體生長受到影響,少量滿足N-W關系[21].然而,個別研究也報道了一些不同結果.Inoue和Koseki[16]采用無填充金屬的焊縫研究了奧氏體不銹鋼中初生鐵素體和奧氏體的凝固過程行為,發現奧氏體在具有胞狀形貌初生鐵素體的枝晶間形成,兩者獨立生長,沒有任何晶體學關系限制.總之,上述的晶體學分析為建立更為準確的聲學仿真模型提供了保證.

圖4 等軸晶中兩相K-S關系 (a)表面取向分布圖;(b){111}γ//{110}α;(c)〈110〉γ//〈111〉αFig.4 .K-S orientation relationship in equiaxial crystal:(a)Surface inverse orientation f i gure;(b){111}γ//{110}α;(c) 〈110〉γ// 〈111〉α.

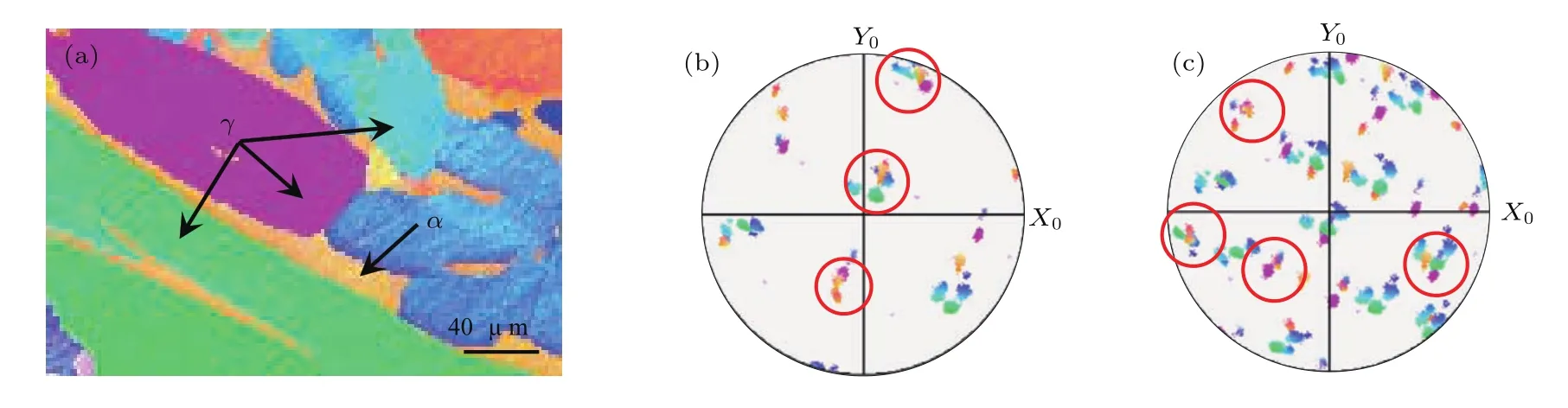
圖5 等軸晶中兩相N-W關系 (a)表面取向分布圖;(b){111}γ//{110}α;(c)〈112〉γ//〈110〉αFig.5 .N-W orientation relationship in equiaxial crystal:(a)Surface inverse orientation f i gure;(b){111}γ//{110}α;(c) 〈112〉γ//〈110〉α.

3.3 考慮兩相位向關系的聲學建模計算

為了分析鐵素體與奧氏體之間位向關系和鐵素體形態對CASS聲學性能的影響,必須建立對應的聲學仿真模型.前期基于EBSD的時域有限差分建模思路已經被證實切實可行,與實驗結果符合較好[10,11].這里以圖3中兩種典型鐵素體形貌為基礎,分別引入K-S和N-W關系,建立二維各向異性時域有限差分模型,研究相同奧氏體取向條件下不同鐵素體形態分布和取向關系對聲傳播的影響.模型左右邊界設為固定邊界,以確保在計算范圍內不會發生波型轉變和超聲波擴散,上下端設為吸收邊界,防止產生額外的反射波而影響計算結果.

材料彈性特性的定量描述是獲得可靠計算結果的關鍵.對于彈性各向異性介質,常用歐拉角φ1,Φ,φ2表示晶體取向與空間坐標軸的旋轉關系,根據Bunge定義[27],三個歐拉角構成的方向余弦矩陣分量如 (1)式所示,進而由R=R1×R2×R3得到如(2)式所示的方向余弦矩陣.

為獲得晶體坐標系下的剛度矩陣,利用Bond變換計算每個奧氏體、鐵素體晶粒對應晶體取向下的彈性常數[28]:

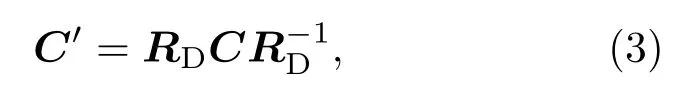
式中,C為樣品坐標系下的剛度矩陣,C′為晶體坐標系下的剛度矩陣,RD為與(2)式方向余弦矩陣R有關的6×6矩陣.RD和R之間的對應關系如(4)式所示,為RD的逆矩陣.

根據已有文獻報道的鐵素體和奧氏體彈性常數[9,11,29],選取成分、組織與本研究相近的情況并取平均值,列于表1,鐵素體彈性常數取C11=230.3 GPa,C12=135.1 GPa,C44=116.6 GPa,奧氏體取C11=265.8 GPa,C12=114.0 GPa,C44=117.1 GPa[9].由上述EBSD結果獲取的歐拉角數據,利用上述理論計算得到對應晶粒取向下的彈性常數,結果如表2所列.鐵素體密度為7897 kg/m3,奧氏體密度為8150 kg/m3[30].

利用有限差分方法計算得到時域A掃描波形后,聲衰減系數β可通過下式計算:

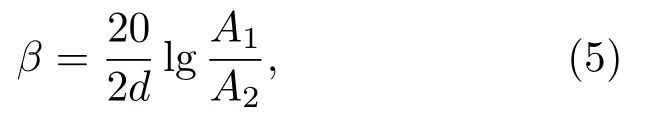
式中d為試樣厚度,A1和A2分別為一次底面回波和二次底面回波的幅度,結果如表3所列.在柱狀晶中,條狀鐵素體形貌對應的K-S關系和N-W關系造成的聲衰減系數差為0.51 dB/mm,島狀鐵素體對應的聲衰減系數差僅為0.1 dB/mm,幾乎相同;根據聲衰減系數差與相同鐵素體形貌下最大聲衰減系數值,得到由位向關系差異導致的相對偏差分別為26%和7%.對于鐵素體形貌的影響,柱狀晶中滿足K-S關系時,條狀鐵素體和島狀鐵素體對應的聲衰減系數差為0.08 dB/mm,N-W關系對應差值為0.49 dB/mm,同理得到相對偏差分別為6%和25%.等軸晶中也存在相似的大小關系,在此不再贅述.需要注意的是,上述位向關系和鐵素體形貌在柱狀晶和等軸晶中均有發現,未見與奧氏體晶粒形態、取向有明顯對應關系,因此必須考慮兩者對CASS超聲衰減的影響,后者更為顯著.

表1 鐵素體彈性常數(單位:GPa)[11,29]Table 1 .Elastic constants of ferrite(unit:GPa).

表2 兩種位向關系中奧氏體和鐵素體對應的歐拉角和彈性常數Table 2 .Euler angles and elastic constants of austenite and ferrite with two orientation relationships.

表3 不同鐵素體形貌下兩種位向關系對應聲衰減系數Table 3 .Attenuation coefficient corresponding to two orientation relationships of dif f erent ferrite morphologies.

4 聲衰減實驗測試與討論

利用水浸超聲脈沖回波技術“原位”獲得圖3柱狀晶兩區域對應的A掃描信號,如圖6(a)所示,并計算聲衰減系數如圖6(b)所示.其中條狀鐵素體形貌對應聲衰減系數為(3.44±0.04)dB/mm,島狀鐵素體形貌對應值為(3.70±0.05)dB/mm.與上述柱狀晶中K-S關系對應模擬結果相比,這里不僅聲衰減系數要高出1—2倍,兩種鐵素體形貌對應大小關系也是相反的,說明實驗中同時存在其他因素的共同作用.

已有研究表明:奧氏體單晶聲衰減行為呈各向異性[31,32],體現為吸收衰減,與介質的黏滯特性、熱傳導特性以及介質微觀過程引起的弛豫效應等密切相關[33].為簡化影響因素,這里僅基于上述結果對〈101〉柱狀晶中聲衰減系數加以討論.Merkulov[34]提出超聲波的散射衰減依賴于超聲波長λ與散射體尺寸D,即根據kD值(k為波數,k=2π/λ),可將散射機理分為三類:瑞利散射、隨機散射和漫散射.Smith[35]給出了超聲散射衰減系數βS與頻率f、散射體尺寸D之間的關系:

其中C1,C2,C3是與材料彈性參數、密度和超聲波波速有關的常數.超聲入射頻率為15 MHz時對應縱波波長約為0.4 mm,因此鐵素體晶粒對應的kD在0.13—4.7之間,聲波散射主要為瑞利散射和隨機散射[36].當kD值較小時(如kD=0.13),單個鐵素體晶粒的散射能力較弱,可以近似為遠場低頻的球散射,對應的散射聲強可以表示為

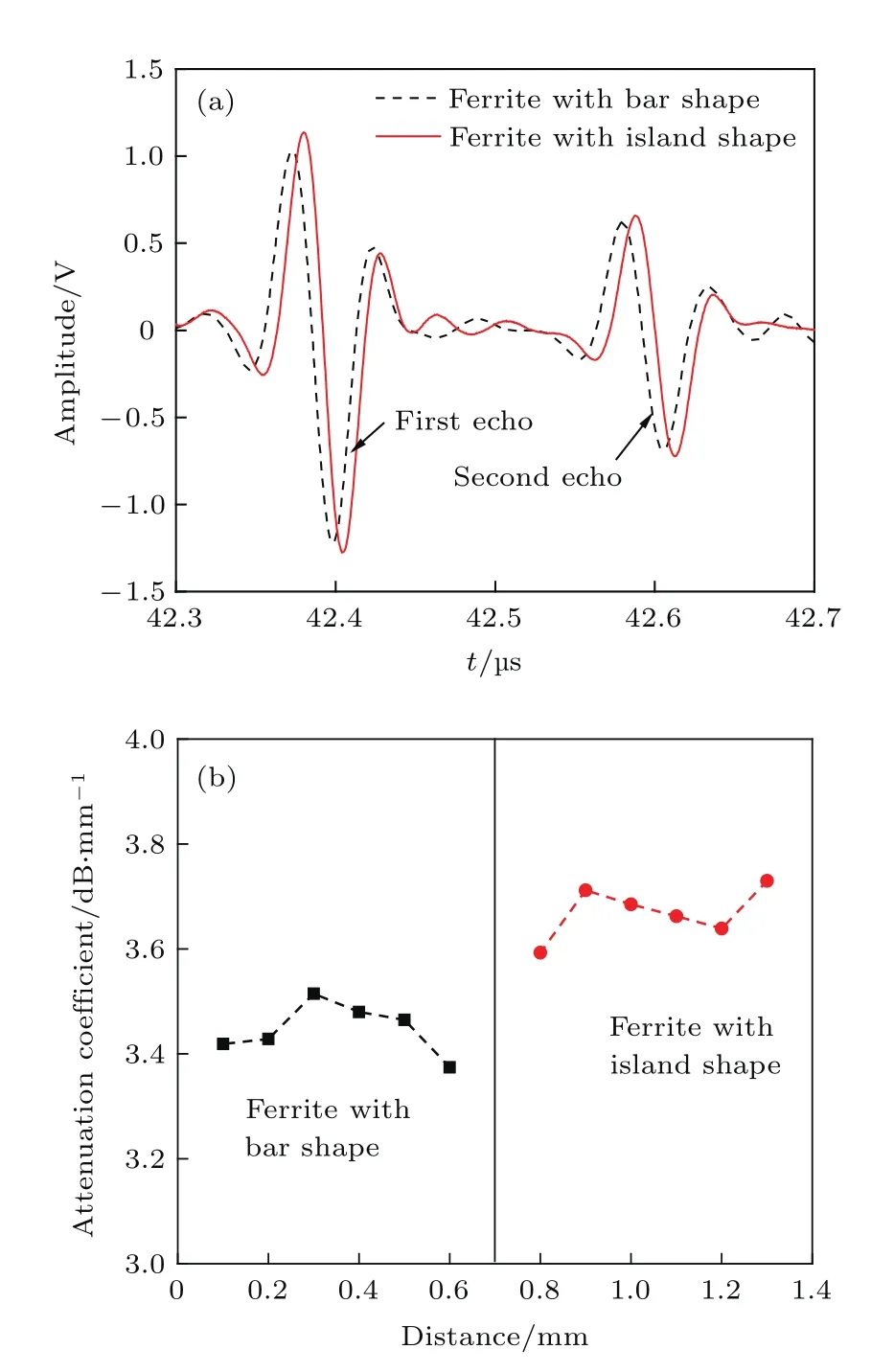
圖6 柱狀晶的聲學測試 (a)實際測量超聲A掃描波形;(b)聲衰減系數測試結果Fig.6 .Ultrasonic testing of columnar crystals:(a)Time domain waveform;(b)attenuation coefficient.

其中pS為散射聲壓;pp為入射波聲壓;ρ為散射體密度;c為散射體中超聲波傳播速度;Ip=|pp(r,θ)|2/(2ρc)為入射波聲強,可由瑞利散射公式計算;θ為鐵素體與聲波入射方向之間的夾角.此時,多個鐵素體晶粒形成散射顆粒群,多重散射總功率可近似認為是所有晶粒散射功率之和.對于kD值較大的情況(如kD=4.7),散射波更加集中在散射體面向入射波的方向,鐵素體晶粒之間的耦合作用更為明顯,必須考慮對總散射功率的疊加效應.

下面對幾種影響因素加以討論.首先,奧氏體與鐵素體位向關系的影響.對應條狀和島狀兩種鐵素體形貌,當位向關系分別為K-S和N-W時,CASS聲衰減系數差分別為0.51 dB/mm和0.1 dB/mm,說明奧氏體與鐵素體的位向關系帶來的聲衰減系數最大偏差約為0.5 dB/mm.其次,鐵素體形貌的影響.對圖3分析發現:條狀鐵素體晶粒平均長徑比為9.3±6.4,與聲波入射方向平均夾角為31?±13?,而島狀鐵素體晶粒平均長徑比為4.7±3.9,僅相當于條狀鐵素體的1/2,與聲波入射方向平均夾角為68?±14?(偏差均為標準差).根據(9)式,同等條件下前者對聲傳播的阻礙作用更強,這一點在N-W位向關系中也得到印證,如表3所列,兩種形貌對應的聲衰減系數偏差為0.49 dB/mm.對應這里的K-S關系,兩種鐵素體形貌帶來的差異很小,體現為(9)式中ρc影響較弱;當鐵素體形貌為島狀時,奧氏體與鐵素體之間位向關系差異帶來的影響也可以忽略,鐵素體晶粒多重散射效應并不明顯.兩種情況充分說明兩相位向關系與鐵素體形貌協同作用影響超聲波傳播,兩個因素的任何一方弱化,都會降低另一因素變化所產生的影響.然而,這與兩因素同時作用又有本質不同:即使在島狀鐵素體、K-S關系情況下,最小的聲衰減系數也在1.2 dB/mm,說明鐵素體對聲衰減的影響不能忽略,約占實測總衰減系數的30%—60%,而鐵素體形貌和兩相位向關系的變化所帶來的影響約占10%—15%.

最后,粗晶奧氏體晶粒內取向不均勻性的影響.針對柱狀晶的模擬和實驗中,實驗所得聲衰減系數要高出約2.0—2.3 dB/mm,占總衰減系數的55%—70%,且兩種鐵素體形貌對應聲衰減系數大小關系相反,原因主要在于粗晶奧氏體內部并不均勻,如圖2所示的EBSD測試結果,即使同一奧氏體晶粒,也存在晶體取向微區的差別.這些微區間造成一定的ρc差,阻礙超聲波傳播.因此,上述EBSD模型除選取相同取向奧氏體晶粒進行比較外,也對奧氏體微區做了均勻化處理,排除奧氏體晶粒內部不均勻性的影響,證實鐵素體對超聲波衰減的影響必須加以考慮.上述三個因素共同作用,影響〈101〉柱狀奧氏體晶粒的聲衰減,對于其他取向晶粒以及不同檢測頻率下聲衰減行為,有待于進一步深入研究.

5 結 論

1)CASS中奧氏體晶粒粗大且不均勻,既有等軸晶又有柱狀晶,且每個奧氏體晶粒中散布著形狀復雜的鐵素體,典型鐵素體形貌為條狀和島狀,差異明顯.

2)利用極圖研究了柱狀晶、等軸晶的奧氏體-鐵素體位向關系,發現CASS中奧氏體-鐵素體位向關系既有滿足K-S關系({111}γ//{110}α,〈110〉γ//〈111〉α)又 有 滿 足 N-W關 系({111}γ//{110}α,〈112〉γ//〈110〉α)的情況,其中以K-S關系為主,少量滿足N-W關系.

3)基于EBSD圖譜建立了考慮鐵素體形貌和奧氏體-鐵素體位向關系的二維聲傳播各向異性模型,發現鐵素體形貌和奧氏體-鐵素體位向關系協同作用影響超聲波傳播.

4)“原位”超聲實驗結果表明:較高檢測頻率(15 MHz)下,對于單一CASS晶粒,奧氏體內部取向不均勻性、奧氏體-鐵素體位向關系以及奧氏體晶粒內鐵素體形貌都會影響超聲散射衰減,其中前者約占總衰減系數的50%以上,其余部分主要為后兩者的協同貢獻.