偶極玻色-愛因斯坦凝聚體在類方勢阱中的Bénard-von Kármán渦街?

席忠紅1)2)3) 楊雪瀅1)2) 唐娜1)2) 宋琳1)2) 李曉霖1)2) 石玉仁1)2)?

1)(西北師范大學物理與電子工程學院,蘭州 730070)

2)(甘肅省原子分子物理與功能材料重點實驗室,蘭州 730070)

3)(甘肅民族師范學院物理與水電工程系,合作 747000)

(2018年8月28日收到;2018年9月26日收到修改稿)

1 引 言

當玻色-愛因斯坦凝聚體(Bose-Einstein condensate,BEC)體系中存在大量渦旋成核時,這些渦旋的排列方式是一個非常值得研究的物理問題[1,2].俄國物理學家Abrikosov[3]在研究超導理論時最先討論了量子化的渦旋結構,并提出了Abrikosov三角渦旋晶格,之后其他物理學家在單分量BEC中也發現了Abrikosov三角渦旋晶格[4].然而,隨著對此類問題研究的不斷深化,研究人員發現,BEC中的渦旋結構不僅僅局限在三角晶格結構[5].實驗和理論研究表明,由于BEC系統受到相互作用、外勢、多分量、旋轉角頻率等諸多因素的影響,系統有更加新奇的渦旋結構[1,5].

當經典流體流過障礙物時,一種普遍而有趣的現象是在尾流中交替產生渦旋對,這就是著名的Bénard-von Kármán渦街[6?8].自從實驗和理論上發現von Kármán渦街以后,物理學家對其做了大量研究.眾所周知,當黏性流體流過障礙物時其行為主要取決于表征流體黏性的雷諾系數Re[6,7],然而,由于超流體無黏性,導致無法定義其黏性系數[9].超流體渦旋的量子化使得其動力學行為與經典流體有很大區別[10],因此在超流體的尾流中能否產生并形成穩定的von Kármán渦街就成為一個有意義的課題.近幾年物理學家就該領域做了大量研究,取得了很多成果.Sasaki等[11]通過數值求解Gross-Pitaevskii(GP)方程,成功模擬了無偶極相互作用BEC尾流中出現的穩定von Kármán渦街,給出了其相圖.Kwon小組[12?14]從實驗上研究了障礙勢在稀薄原子氣體BEC中運動時尾流中的von Kármán渦街.Sasaki等[15]研究了雙組分BEC中分離相的動力學行為,發現在強相分離情形下,組分1的原子在組分2中運動時會分裂成量子化渦旋并在尾流中形成von Kármán渦街.

當超冷原子氣體的電偶極或磁偶極的相互作用不可忽略時,須考慮原子間的偶極效應.偶極效應遠比各向同性的s波作用復雜得多,是一種長程各向異性的相互作用,會對超冷原子氣體的基態相圖、穩定性以及動力學行為產生重要影響[15?19].此外,偶極間的各向異性相互作用也提供了一個可控參量,使得偶極凝聚體在量子模擬和計算等許多高水平的研究領域有了應用的可能[20].但據我們所知,偶極BEC中的渦街現象一直未有報道.

本文對偶極BEC在類方勢阱中的Bénard-von Kármán渦街現象進行了數值研究.結果表明,當障礙勢在BEC中的運動速度與尺寸在適當范圍內時,系統中會出現穩定的兩列渦旋對陣列,即Bénard-von Kármán渦街.本文也研究了偶極相互作用強弱、障礙勢尺寸以及運動速度對尾流中產生的渦旋結構的影響,得到了相圖結構,并對障礙勢所受拖拽力進行計算,分析了渦旋對產生的力學機理.

2 理論模型

考慮質量為m的偶極原子BEC束縛在勢阱Vext中,障礙勢VOP在BEC中沿x方向以速度υ運動.設原子沿軸n=(nx,ny,nz)極化,其中在平均場近似下,可以得到描述系統的GP方程[19?22]

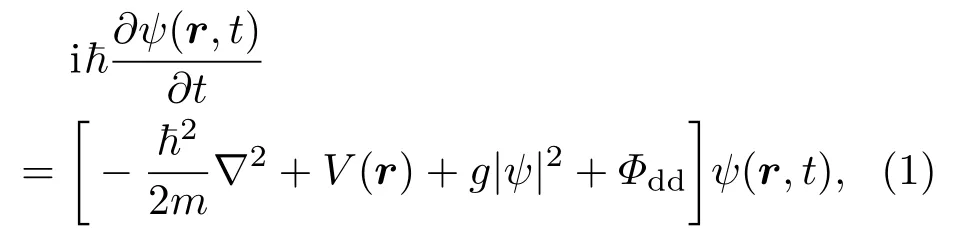
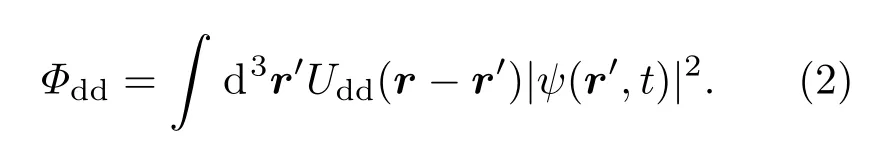
偶極相互作用為

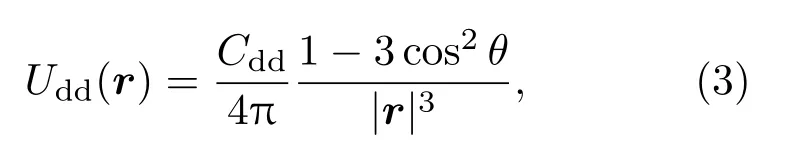
實驗中,BEC原子通常被置于諧振子勢阱中.若諧振子勢頻率滿足ωz?ωx,ωy,則BEC將被束縛在xoy平面內.此時,可先進行準2維近似[22],然后進行無量綱化處理:,并略去變量上的”～”號,其中,ω0= ωx,從而得無量綱化準二維GP方程[25]

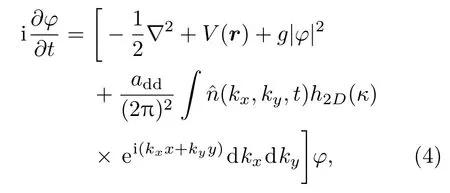
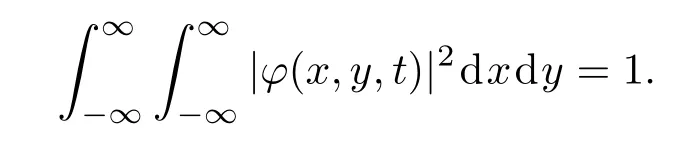
方程(4)中

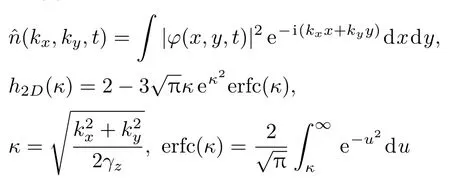
為完全誤差函數,γz=ωz/ω0.

數值計算針對方程(4)進行,計算范圍取為{(x,y)||x|<512,|y|<128}.用φ=1作為初始波函數,利用虛時演化法[26]得到系統的基態.然后取該基態作為初始條件,利用時間劈裂傅里葉譜方法[27]對GP方程(4)進行非線性動力學演化,從而對系統的動力學行為進行研究.

3 數值結果

考慮外勢為下面的類方勢阱[28]

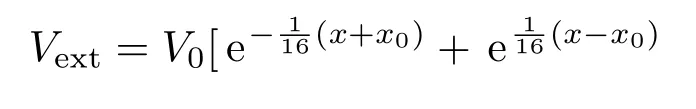
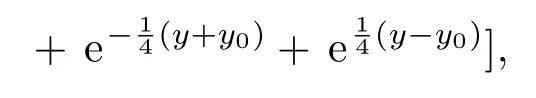
其中V0是無量綱化的外勢深度;±x0,±y0分別表示x,y方向上阱壁所在位置.該勢阱的特點是在阱壁處勢很強而阱內離開阱壁處勢很快降為接近于0,故可視為對無限深方勢阱的一種近似.當V0=1000時外勢形狀如圖1所示.

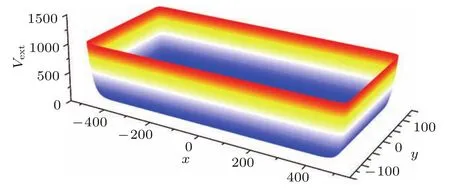
圖1 外勢形狀圖 (取外勢深度V0=1000,阱壁位置x0=512,y0=128)Fig.1 .Shape of external potential(The depth of external potential is V0=1000,and the position of a potential wall is x0=512,y0=128).

將N=2.5×105個164Dy原子BEC束縛在該勢阱中,164Dy原子磁偶極矩為10μB(μB為玻爾磁子),原子質量m=2.72×10?25kg.取諧振子勢頻率(ωx,ωy,ωz)=2π×(4.3,56,350)Hz,這與Berkeley等團隊的實驗參數一致[11].由此可得偶極相互作用系數add≈0.2.通過Feshbach共振調節s波散射長度使as≈8.0×10?13m時,由得g≈1.故在計算中取add=0.2,g=1.考慮無量綱化的圓柱形障礙勢

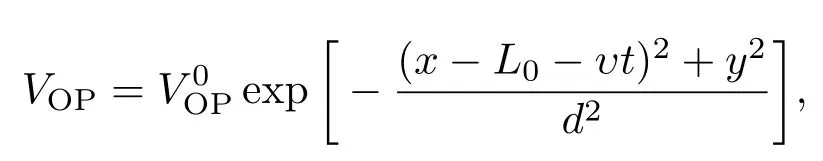
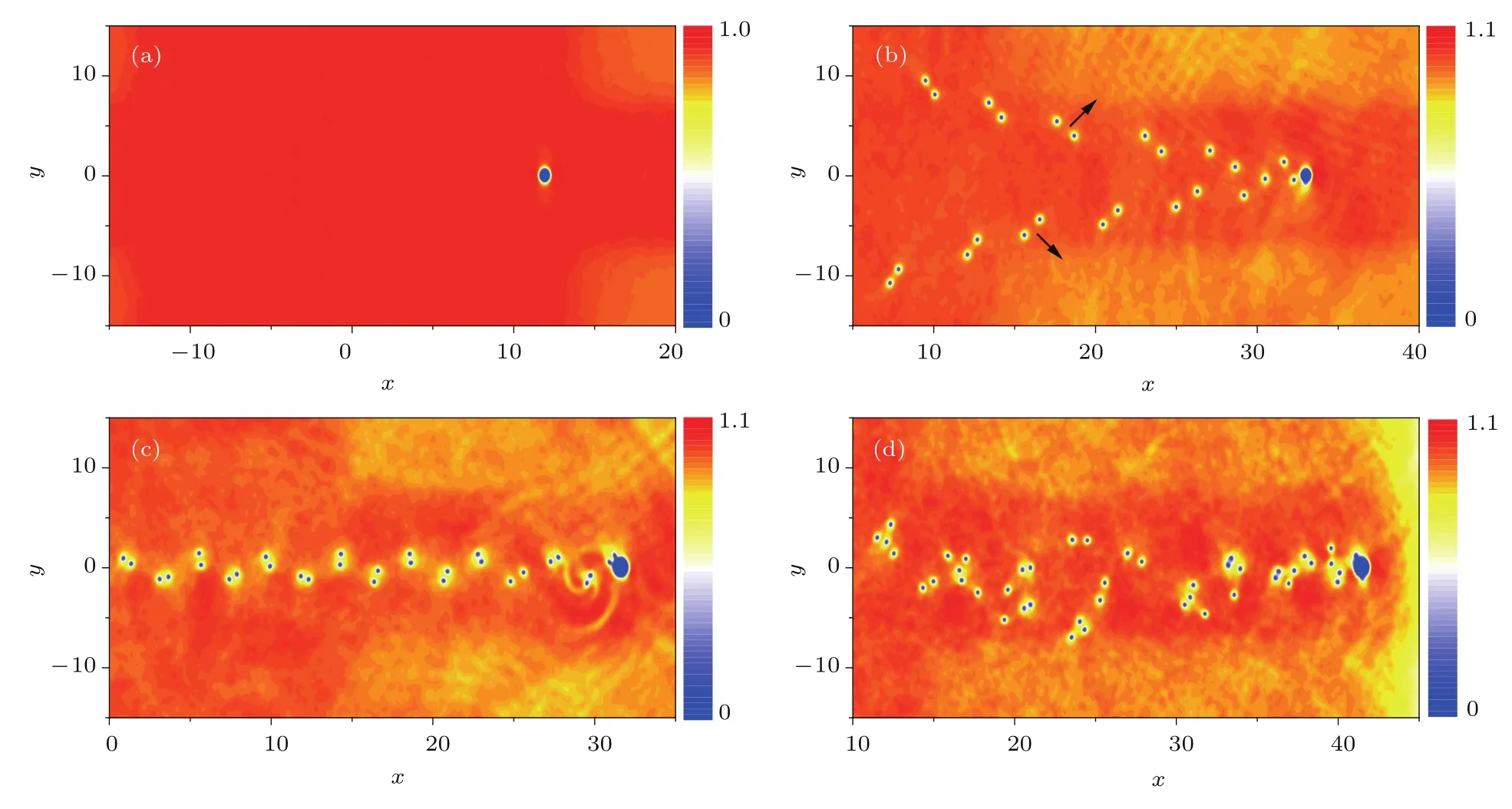
圖2 障礙勢在偶極BEC中運動時尾流密度分布 (a)υ=0.25,d=1.2;(b)υ=0.49,d=1.2;(c)υ=0.48,d=1.8;(d)υ=0.55,d=1.82Fig.2 .Density distributions of a condensate past an obstacle potential:(a)υ=0.25,d=1.2;(b)υ=0.49,d=1.2;(c)υ=0.48,d=1.8;(d)υ=0.55,d=1.82.

從圖2可以看出,當障礙勢的運動速度υ足夠小時,障礙勢周圍的凝聚體是穩定的層流形式,沒有渦旋產生(圖2(a)).當障礙物勢的運動速度υ達到某個臨界值時,尾流中開始產生如圖2(b)所示的渦旋-反渦旋對.這個臨界值主要取決于障礙物勢的形狀和原子之間的相互作用[9].當一對渦旋從障礙勢脫落后,附近的凝聚體很快達到產生渦旋的臨界條件并產生新的渦旋對,這樣就在障礙勢后面產生了上下兩列渦旋對陣列.由于一個渦旋對中的兩個點渦旋有著不同的旋量±h/m(h為普朗克常量),使得兩列對稱分布的渦旋對陣列不穩定[11].受到小的擾動時,渦旋對會沿著垂直于渦旋對連線的方向(圖2(b)黑色箭頭所示方向)平動,從而在尾流中形成V字形渦旋對陣列結構.一些學者在研究經典流體時也發現了這種交替的渦旋模式[29?31].這種渦旋結構在υ比較大、d比較小時更加明顯,與經典流體中的尾流模式非常類似[11].

當障礙勢的運動速度υ增大到一定程度并且障礙物的尺寸d在適當范圍內時,其后同時產生的一組渦旋對具有相同的旋量h/m或?h/m,以角頻率2~/(md20)繞著它們的中心運動[11],在運動過程中兩個點渦旋之間的距離d0基本保持不變.這樣,在尾流中交替產生的旋量相反的渦旋對就形成穩定的兩列渦旋對陣列,即Bénardvon Kármán渦街(圖2(c)). 在圖2(c)參數條件下,數值計算得到上下兩列渦旋陣列之間的距離b≈19a0,同一陣列中兩個渦旋對之間的平均距離?≈68a0,因此b/?≈0.28.該值與經典流體中Bénard-von Kármán渦街產生的穩定性條件以及Sasaki等在研究無偶極相互作用BEC時的結論一致.當障礙勢的運動速度υ繼續增大時,障礙物勢后尾流中的這種周期性渦街消失,在尾流中出現混亂的渦旋結構(圖2(d)).

為研究各種尾流結構的參數區間,我們對系統在不同υ和d時的情形進行了大量數值計算(圖3為其相圖結構).

圖3 尾流結構隨障礙勢尺寸d和運動速度υ的變化Fig.3 .Dependence of the patterns of wakes on the normalized width d and velocity υ of the obstacle potential.

從圖3可以看出,沿圖中箭頭所示方向改變參數時,障礙物勢后尾流的結構依次出現穩定的層流、渦旋對、von Kármán渦街以及混亂的渦旋結構,分別與圖2(a)—(d)相對應.顯然,von Kármán渦街出現的參數范圍相對較小,具體約為1.0 6 d 6 3.4,0.37 6 υ 6 0.54.圖3與無偶極相互作用時的相圖結構也存在較大不同.在無偶極相互作用的BEC中(add=0),d>1.5時,尾流從穩定的層流直接過渡到卡門渦街或者混亂模式,而不會出現圖3中較寬范圍的渦旋對結構.同時,隨著偶極相互作用強度的增加,相圖中von Kármán渦街出現的參數區域變得更窄.然而,對于經典流體,在雷諾數Re變化的較大范圍內都會出現von Kármán渦街[32?35].

以上數值結果容易在實驗中得以實現.考慮將N=2.5±0.5×105個164Dy(磁偶極矩為10μB)或52Cr(磁偶極矩為6μB)或168Er(磁偶極矩為7μB)等原子BEC束縛在方勢阱中,取諧振子勢頻率(ωx,ωy,ωz)=2π × (4.3,56,350)Hz[11]. 此時,偶極相互作用系數add≈0.2.通過Feshbach共振調節s波散射長度使接觸相互作用系數g≈1.當尺寸

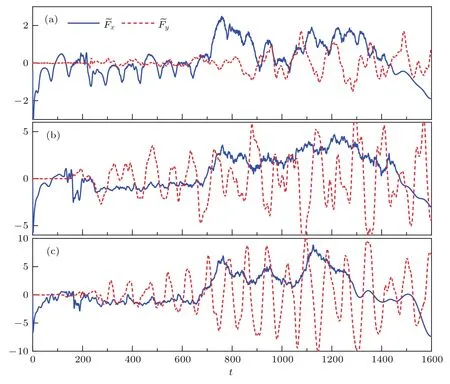
圖4 無量綱化拖拽力?F隨時間的變化(a)υ=0.49,d=1.2;(b)υ=0.48,d=1.8;(c)υ=0.55,d=1.8Fig.4 .Time evolution of the normalized drag force?F:(a)υ=0.49,d=1.2;(b)υ=0.48,d=1.8;(c)υ=0.55,d=1.8.

為1.0a06 d 6 3.4a0的激光束以速度在偶極BEC中運動時,將會在激光束后尾流中周期性產生渦旋對,形成穩定的Bénard-von Kármán渦街.

若考慮將N=2.0±0.5×103個164Dy原子BEC束縛在類方勢阱中,通過Feshbach共振調節s波散射長度as=4.08×10?9m ≈ 77aB,aB為玻爾半徑.此時接觸相互作用系數g≈100,偶極相互作用系數add≈20(其他參數與前面相同),仍有add/g=0.2.數值結果表明,此時也會出現圖2(c)中所示的Bénard-von Kármán渦街現象.

4 結 論

對偶極BEC在類方勢阱中的Bénard-von Kármán渦街現象進行了研究.在平均場近似下,通過虛時演化法得到系統的基態,然后利用時間劈裂傅里葉譜方法對系統進行非線性動力學演化,發現障礙勢在偶極BEC系統中以一定速度運動時,系統中會出現穩定的兩列渦旋對陣列,即Bénardvon Kármán渦街;數值研究了偶極相互作用強弱、障礙物勢尺寸以及運動速度對尾流中產生的渦旋結構的影響,得到了系統的相圖結構;通過對障礙勢所受拖拽力進行計算,分析了渦旋對產生的力學機理.