特征函數(shù)的性質在實變函數(shù)中的應用

石秀文

（邢臺學院，河北邢臺 054001）

在實變函數(shù)中討論集合的基數(shù)與對等、可測函數(shù)及函數(shù)的積分等問題時，常常用到特征函數(shù)，如果熟悉特征函數(shù)常用性質，并能熟練掌握應用特征函數(shù)的性質解決問題的一般思想，有助于提高學生分析問題和解決問題的能力。下面將探討利用特征函數(shù)的性質解決實變函數(shù)中某些問題中一般思想方法。

1 特征函數(shù)及常用的一些性質

1.1 特征函數(shù)的定義

顯然，若A是可測集S的可測子集，φA（x）則是S上非負可測函數(shù)，也是可積函數(shù)且

1.2 常用的幾個特征函數(shù)的性質

性質 1：設 A，B?S，則 A?B?φA（x） ≤φB（x），x∈S（單調性），φA（x）＝φB（x），x∈S?A=B（一對一性質）。

性質2：（特征函數(shù)與簡單函數(shù)的關系） 若f（x）=ci，x∈Ei，i=1，2…n，是 E 上的簡單函數(shù)，則 f（x）互不相交。

性質4：（積分等式）若f（x）在可測集E的可測子集E0及收斂，可測子集列En上可積，則有等式

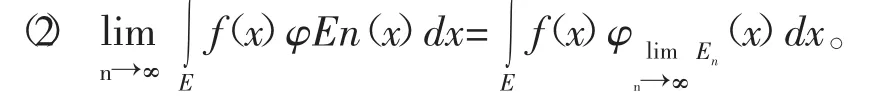
2 特征函數(shù)性質的應用

2.1 “一對一性質”在集合對等問題中的應用

集合的基數(shù)是集合的重要屬性，研究集合的基數(shù)是通過集合對等的關系來確定，建立集合間的——對應關系是確定對等的基本方法，如果難于建立集合間的一一對應關系，常用Bernstein定理來判斷對等并確定其基數(shù)。特征函數(shù)與集合間的一對一性質，對討論某些集合間對等有著重要的作用。

例1：設S是可數(shù)集，S的所有子集構成的集合為2S，求2S的基數(shù)。

解：由集合對等與基數(shù)的定義可知：對等集合的所有子集構成的集合族仍對等。不妨設為非負有理數(shù)集合為 S＝ ｛r1，r2，…rn，…… ｝，?A∈2S，令

設 φA（rn）=an，n＝1，2，3，……；令 x＝0.a1，a2，a3……，則 0≤x＝0.a1，a2，a3……＜1，即 x∈[0，1]。

由一對一性質，2S與 [0，1]的一個子集對等，所以（c為[0，1]的基數(shù)）。

反之，對?x∈[0，1]，可表示為唯一的無限小數(shù)0.b1，b2，b3……，可設對應的非負有理數(shù)構成的集

顯然，此映射是一對一的，故 [0，1]與2S的一個子集對等，所以綜上。

由此可見，通常討論某集的所有子集構成的集合2S的基數(shù)問題或集合族與其他集合對等問題時，可考慮應用定義在S上關于其子集的特征函數(shù)，通過特征函數(shù)“一對一”性質，建立2S與相關集合或其子集的一一對應關系來解決問題。

2.2 可測函數(shù)與特征函數(shù)的關系的應用

可測函數(shù)與簡單函數(shù)的關系：f（x）是可測集E?Rn上可測函數(shù)的充要條件是存在一列簡單函數(shù)ψm（x），使得

而由性質2可知簡單函數(shù)ψm（x）是一組特征函數(shù)的線性和。因此，討論可測函數(shù)問題，就可以歸結為最簡單的特征函數(shù)問題，“由特征函數(shù)到簡單函數(shù)，再向一般可測函數(shù)過度，這在許多場合都是行之有效的辦法。”

例 2：設 f1（x）、f2（y）分別是 E1?Rp、E2?RqS上可測函數(shù)，證明：f1（x）×f2（y）是 E1×E2?Rp×Rq上可測函數(shù)。

解析：證明有具體表達式函數(shù)的可測性，用定義直接證明較為簡便；證明抽象函數(shù)可測性，可考慮用“可測函數(shù)與特征函數(shù)的關系”進行推理論證。

設f（x，y）=f1（x）×f2（y）

（1）若fi（x）是可測子集Ei上特征函數(shù)，則f（x，y）是E1×E2上特征函數(shù)，可測集上特征函數(shù)是可測函數(shù)，故結論成立。

（2）若fi（x）是Ei簡單函數(shù)，則f（x，y）是E1×E2上簡單函數(shù)（易證），故是可測函數(shù)。

（3）fi（x）是一般可測函數(shù)，由可測函數(shù)與簡單函數(shù)的關系，存在簡單函數(shù)列 gm（x），hm（y），使得：f1

令 ψm（x，y）=gm（x）×hm（y），也是 E1×E2上簡單函列，且

故結論成立。

此例證明思路是由簡單到復雜，即由特征函數(shù)成立——簡單函數(shù)成立——一般可測函數(shù)成立，這種由特征函數(shù)逐漸遞進到一般可測函數(shù)的證明，是實變函數(shù)中常用的方法。

2.3 特征函數(shù)積分性質的應用

設f在E及其可測子集E0上可積，常用的兩個等式：若存在，由控制收斂定理及極限性質：

證明：對任意可測子集A?E，φA（x） 在E有界可積，故由A的任意性可知：

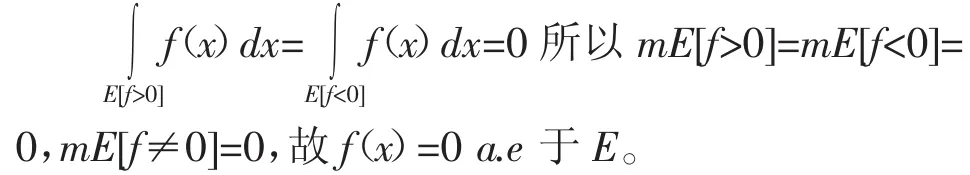
可見利用等式（1）通過特征函數(shù)巧妙的將E上的積分轉化為其任何子集上的積分使其為零，體現(xiàn)了特征函數(shù)在積分問題中的作用。一般的，當涉及到某集合上的積分與之子集上的積分關系時，可考慮應用這一性質進行轉化。

例4：設函數(shù)f在E上可積，可測集列En?存在，則

（2） 由可積性知，f在En上可測，而[a，b]，故 f在 [a，b]上可測.構造函數(shù)列：fn（x）＝φEn則fn（x）在E上可測，由En?En+1，由特征函數(shù)單調性，可知 fn（x）≤fn+1（x），所以 fn（x）→f（x）于E。

例6：若設f，g在可測集E上非負可測，則對?a∈R1，mE（f≥a）＝mE（g≥a），則

解析：E＝E[x；f（x）≥0]＝E[x，g（x）≥0]，

（2） 否則f，g在E上幾乎處處有限（不妨設處處有限），由已知條件可知：mE（a≤f≤b）＝mE（a≤f）-mE（b≤f）＝mE（a≤g≤b），?a，b∈R1。于是?n，令 En＝E[0≤f≤n]＝E[0≤g≤n]，F(xiàn)n＝E[n≤f]＝E[n≤g]，E＝En∪Fn

?n，將En作互不相交分解：其中，令 Fn＝En，n2*，由集En，k的特征函數(shù)來構造E上單調遞增簡單函數(shù)列：（x），則?x∈E，?n，使得f（x）∈[0，n]

此例中，利用特征函數(shù)構造如上的簡單函數(shù)列，該函數(shù)列在E上收斂于可測函數(shù)f（x），這是實變函數(shù)中特征函數(shù)應用的一個典型的方法，對討論某些可測函數(shù)與積分問題有著重要作用。