例談圓錐曲線中最值與范圍問題的解決策略

（甘肅省民勤縣第一中學 甘肅民勤 733300）

圓錐曲線中最值與范圍問題一直是高考中的熱點和難點，其中有不少試題涉及到最值與范圍，對于這些問題，很多同學望而生畏，騎虎難下，深感困難重重，難以決策。這類問題，也并非無規可尋，下面通過幾個典型題目談談解決圓錐曲線中最值與范圍問題的策略。

題型一：最值問題

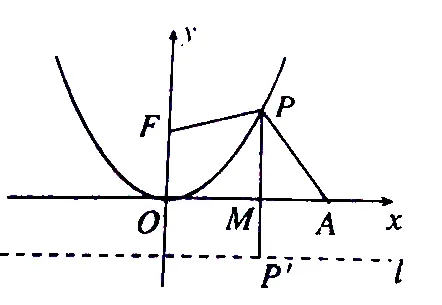
根據拋物線的定義知，|PP′|=|PF|，

[講評]一看到本題，不少同學可能會依常理“出版”——構造函數，將問題轉化為求函數的最值，然而其最值很難求得，這也恰恰落入了命題者有意設置的“圈套”之中，事實上，與拋物線的焦點（或準線）相關的最值問題，更多的是考慮數形結合，利用拋物線的定義進行轉化，然后再利用三點共線或三角形的三邊關系加以處理。

探究1 圓錐曲線中最值的求法有兩種：

（1）幾何法：若題目的條件和結論能明顯體現幾何體特征及意義，則考慮利用圖形性質來解決，這就是幾何法。

（2）代數法：若題目的條件和結論能體現一種明確的函數，則可首先建立起目標函數，再求這個函數的最值，求函數最值的常用方法有配方法、判別式法、重要不等式法及函數的單調性法等。

題型二 范圍問題

（2）若|AP|=|OA| ，證明直線OP的斜率k滿足|k|>

[解析]（1）設點P的坐標為（x0，y0），由題意，有

APBP00(a2-2b2)y02=0。由于y0≠0，

故 a2=2b2，于是所以橢圓的離心率

（2） 依題意，直線OP的方程為y=kx，設點P的坐標為（x0，y0），

消去y0并整理得

由|AP|=|OA|，A（-a，0）及y0=kx0，得

2>4k2+4，即k2+1>4。因此k2>3，所以|k|>

探究2 求參數范圍的常用方法有四種：

（1）函數法：用其他變量表示該參數，建立函數關系，利用求函數值域的方法求解。

（2）不等式法：根據題意建立含參數的不等式，通過解不等式求參數的范圍。

（3）判別式法：建立關于某變量的一元二次方程，利用判別式Δ求參數范圍。

（4）數形結合法：研究該參數所表示的幾何意義，利用數形結合思想求解。