基于改進型顯性互補濾波的MENS姿態解算

付 雷，章 政，余 義

（武漢科技大學 信息科學與工程學院，武漢 430080）

對于移動機器人、飛行器和衛星通信等系統而言，實時、準確的姿態估計是實現各種載體穩定運行的有效前提之一。

目前，由低成本、小型化的微機械陀螺儀、加速度計等慣性測量單元IMU（inertial measurement unit）構成的微機電系統MEMS（micro-electro-mechanical system）姿態估計得到了廣泛的研究和應用。然而在實際應用過程中，單一的IMU易受到噪聲、溫度漂移及安裝誤差等多方面因素影響[1]。因此，將不同的傳感器進行優勢互補，形成多傳感器融合系統用于保證載體姿態的精度和實時性。

1 多傳感器融合系統的研究現狀

低成本STM32處理器的四旋翼飛行器試驗測試平臺，將所設計的算法進行靜態試驗和動態試驗，以驗證所設計系統的有效性。

在多傳感器融合系統中，通常是以卡爾曼濾波算法為基礎的擴展和衍生算法或者互補濾波算法，將多種IMU傳感器的信息進行融合，由此提高載體姿態的精度和抗干擾性。文獻[2]設計了一種卡爾曼濾波算法，將加速度及磁航向作為觀測量對姿態信息及陀螺儀的漂移進行修正；文獻[3]提出了一種擴展卡爾曼濾波算法，將測量噪聲和系統噪聲引入狀態方程，提高了姿態解算精度，但在觀測方程線性的時候引入了誤差；文獻[4-5]提出了一種無跡卡爾曼濾波算法，解決了線性化帶來的誤差，相比擴展卡爾曼精度更高；文獻[6]設計了一種互補濾波算法，無需對噪聲進行精確建模，從頻域的角度上消除誤差并進行數據融合。在此基礎上，文獻[7-8]提出了一種顯性互補濾波ECF（explicit complementary filter）算法，在互補濾波算法的補償環節中加入了積分器，直接對IMU所測的矢量數據進行融合。文獻[9]提出一種具有增益調節機制的顯性互補濾波器，使得基于重力加速度估計的互補濾波器，能獲得較為精確的姿態估計。文獻[10]給出了一種自適應顯性互補濾波算法，根據加速計的輸出，判斷載體的運動情況，實時調整PI參數，以提高姿態估計的精度。

對于以卡爾曼濾波算法為基礎的信息融合方法，由于載體姿態變量的非線性、觀測方程的求解，以及系統噪聲和測量噪聲序列方差陣的計算，其繁瑣的計算過程對處理器的運算速度和要求都較高，對于MEMS的實際工程應用難度較大。

相對而言，以互補濾波為基礎的相關算法既可解決單一傳感器無法準確估計姿態的問題，也無需對姿態估計進行重構，更適用于嵌入式硬件平臺。

鑒于此，文中設計了一種加速度計/陀螺儀組合導航的改進型顯性互補濾波姿態解算算法。首先，對加速度計量測數據的白噪聲進行處理，再將其與陀螺儀數據融合進行姿態解算，由此減小白噪聲對姿態解算精度的影響。然后，為了解決濾波后加速度數據對姿態解算的實時性造成的影響，設置緩存區保存更新后的四元數向量，在緩存區中取出與加速度對應時刻的四元數向量進行數據融合。最后，搭建了基于

2 系統姿態描述

在載體的運動狀態描述中，定義的導航坐標系（參考坐標系）n系和載體坐標系b系如圖1所示。其中，導航坐標系選取“東-北-天”建立坐標系，坐標原點為O點；載體坐標系選取右手直角坐標系，即向右為X正方向，向前為Y軸正方向，向上為Z軸正方向，其坐標原點O′與導航坐標系原點重合。

圖1 導航坐標系和載體坐標系Fig.1 Navigation coordinate system and carrier coordinate system

在此選用計算量小、算法簡單的四元數更新算法[11]實現載體的姿態估計。四元數定義為

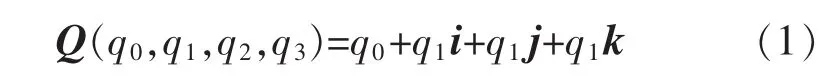
式中：q0，q1，q2，q3為實數；i，j，k 為互相正交的單位向量，且為虛單位

載體的姿態分別用繞Z軸旋轉為偏航角（yaw）ψ，繞Y軸旋轉為橫滾角（roll）θ，繞X軸旋轉為俯仰角（pitch）φ來描述，且按照ψ→θ→φ的旋轉順序。將四元數轉化為歐拉角形式的方向余弦矩陣為

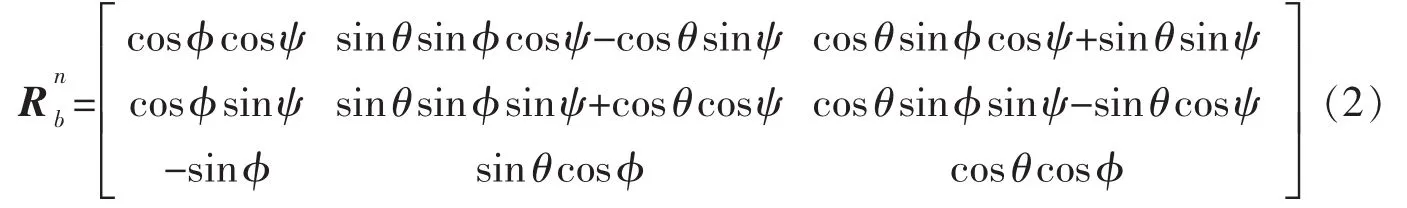
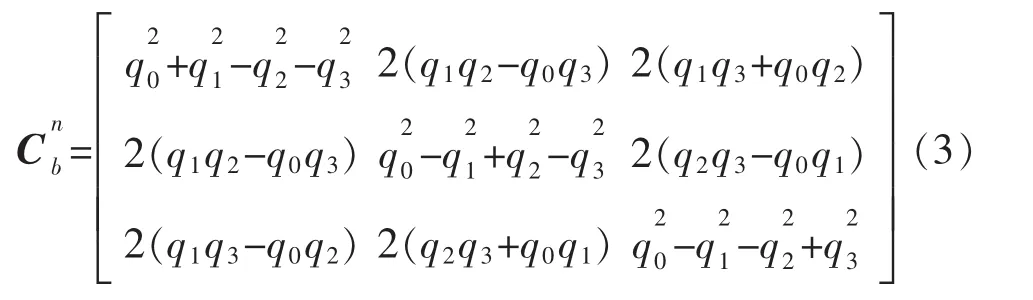
由式（2）（3）可得，四元數與歐拉角的關系為

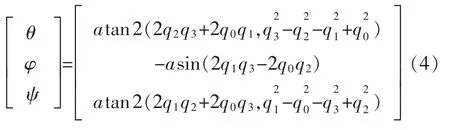
3 基于改進顯性互補濾波器姿態估計算法

3.1 陀螺儀姿態更新算法

四元數的運動學微分方程為

其中

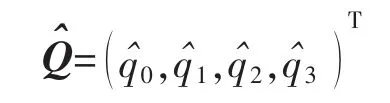
由式（5），可得載體的四元數更新等式為

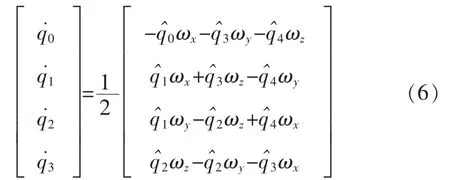
假設，四元數更新時間及采樣時間為T，在時間間隔（t，t+T）內，ω 為常數，載體四元數的更新迭代公式為

式中：i=1，2，3；Δts為系統采樣時間。

根據更新后t時刻的四元數，可得到載體的旋轉矩陣，由式（4）得到t時刻載體的姿態角。

3.2 改進顯性互補濾波器設計

顯性互補濾波器是在速度計/陀螺儀互補濾波算法的補償環節中加入積分環節，由此補償陀螺儀產生的漂移誤差。同時，為了減小加速度原始數據中白噪聲對姿態解算精度造成的干擾，在顯性互補濾波算法的基礎上，消除低通濾波器延時給姿態解算實時性帶來的影響，文中所設計的改進顯性互補濾波算法如圖2所示。

利用該算法進行四旋翼姿態解算的具體步驟如下：

初始化四元數，令

圖2 改進顯性互補濾波器Fig.2 Improved explicit complementary filter

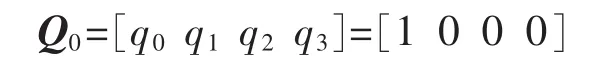
將測得的載體坐標系下的加速度A′經過巴特沃斯低通濾器后進行標準化，得到載體坐標系下三軸加速度的分量構成的向量

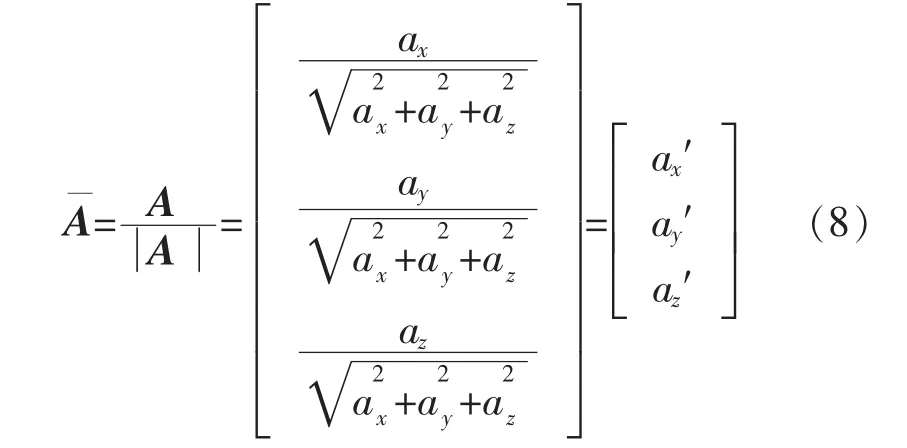
式中：ax′，ay′，az′分別為三軸加速度分量。 但信號經過巴特沃斯低通濾波器之后存在延時，這種特性稱為濾波器的群時延，其定義[12]為

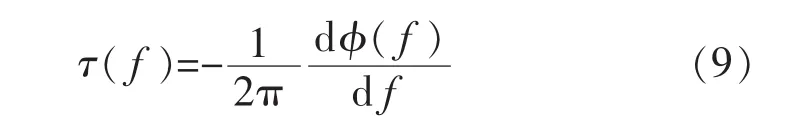
式中：φ（f）為濾波器相位響應；f為頻率。為了消除群時延對姿態解算實時性的影響，需求出延時時間。通過式（9）計算出加速度延時時間為Δt，在緩存

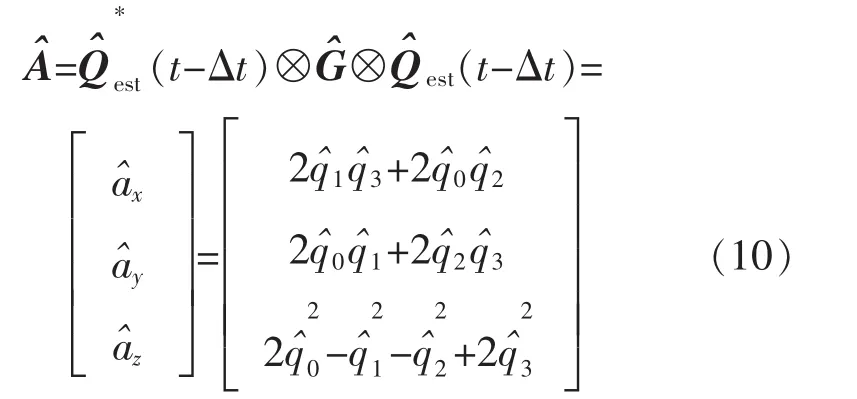
其中

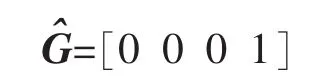
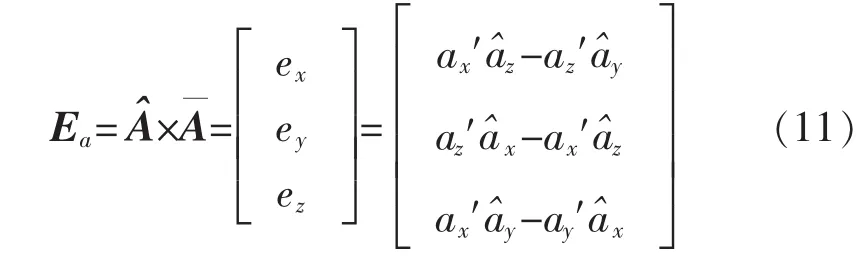
為了對陀螺儀的輸出進行預測矯正，誤差向量經過PI環節得到的校正量δ為

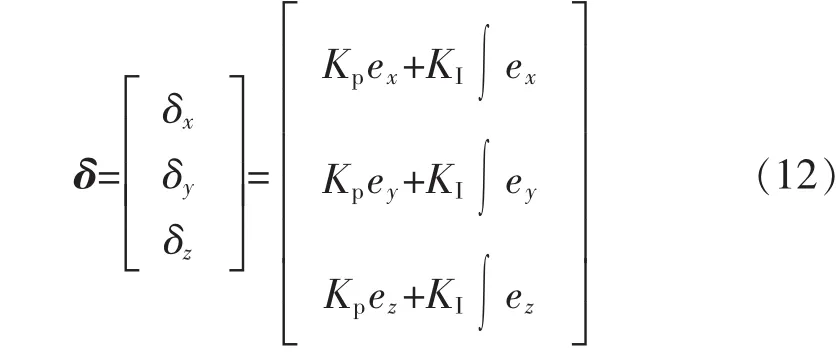
顯示互補濾波器的效果與KP，KI的選擇有很大的關系，如果參數不合適，則姿態估計的誤差較大，甚至偏離實際值。KP為低通濾波器和高通濾波器的之間的轉接頻率，根據加速度計的輸出A′和陀螺儀的輸出ω的頻率特性來選取；KI為積分增益，其值為Kp的幾十或幾百分之一。

最后，將陀螺儀測得的角速度與式（11）中所求的校正量相加，得到補償后的三軸角速度為

將補償后的三軸角速度代入式（6），求得更新后的姿態四元數微分；利用式（7）對四元數微分進積分，積分時間為采樣周期，根據更新后的四元數可得到對應的旋轉矩陣，進而通過式（4）得到四旋翼的姿態角 θ，ψ，φ。

4 試驗測試平臺

文中所搭建的四旋翼飛行器試驗測試平臺如圖3所示；建立了上位機、飛行器和遙控器通訊，系統結構如圖4所示。

圖3 四旋翼飛行器實物Fig.3 Four-rotor aircraft object

圖4 飛控系統結構Fig.4 Flight control system structure

圖4中，四旋翼飛行器的控制單元由主控模塊、慣性測量模塊、穩壓模塊、電源模塊、電機驅動模塊和無線通訊模塊構成。其中，主控模塊選用ST公司的基于ARM-CortexM3內核的STM32F103RCT6芯片。慣性測量模塊選用美國Inven Sense公司的三軸陀螺儀和三軸加速度計集成芯片MPU6050，與主控模塊通過IIC進行通訊。無線通訊模塊選用富斯公司的10通道2.4 GHz遙控器與PPM接收器，以及2.4 GHz無線數傳模塊，PPM信號通過單個I/O口就能與主控通訊，無線傳輸距離可達700 m，無線數傳模塊通過串口與主控模塊通訊，發送實時姿態數據到上位機。電機驅動模塊則利用PWM控制電子調速器的輸出來驅動無刷電機。四旋翼飛行器的各項參數見表1。

表1 四旋翼飛行器參數Tab.1 Parameters of quadrotor

5 試驗結果及分析

為了測得噪聲的頻率范圍，讓四旋翼飛行器處于懸停狀態，對加速度計的原始測量值進行采集，將采集到的數據通過USART上傳到上位機，并進行FFT變換。根據頻譜分析，可以確定截止頻率約為20 Hz，所以試驗選用了截止頻率為20 Hz的二階巴特沃斯數字低通濾波器來進行噪聲處理。采用MatLab仿真出幅頻和相頻特性曲線，如圖5所示。根據3.2的分析，由式（9）可求得延時時間約為64 ms。

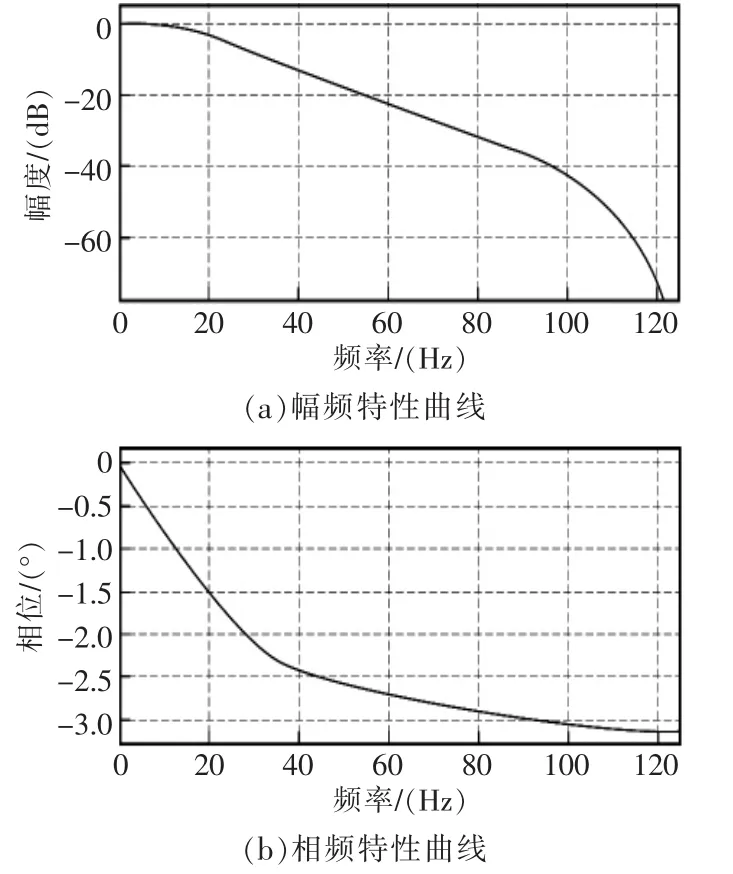
圖5 低通濾波器幅頻和相頻特性Fig.5 Amplitude-frequency and phase-frequency characteristics of low-pass filters

為驗證改進型顯性互補濾波算法的實時性和準確性，進行了2組試驗：第1組為靜態試驗，測試算法的精確度和靜態性能；第2組為動態試驗，測試算法在不同角速度下的實時性和動態性能。

當試驗平臺靜止時，分別用標準型顯性互補濾波算法和改進型互補濾波ECF算法，解算出四旋翼飛行器的姿態，并記錄橫滾角和俯仰角（如圖6所示）。由圖可見，靜態測試標準ECF算法中橫滾角和俯仰角的波動范圍為-0.1～0.1；改進ECF算法中橫滾角和俯仰角的波動范圍為-0.1～0.1。

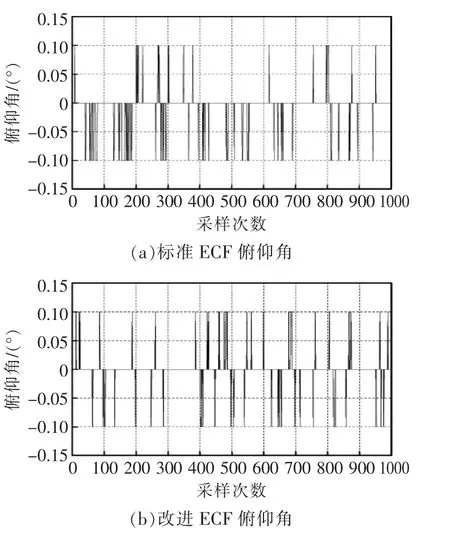
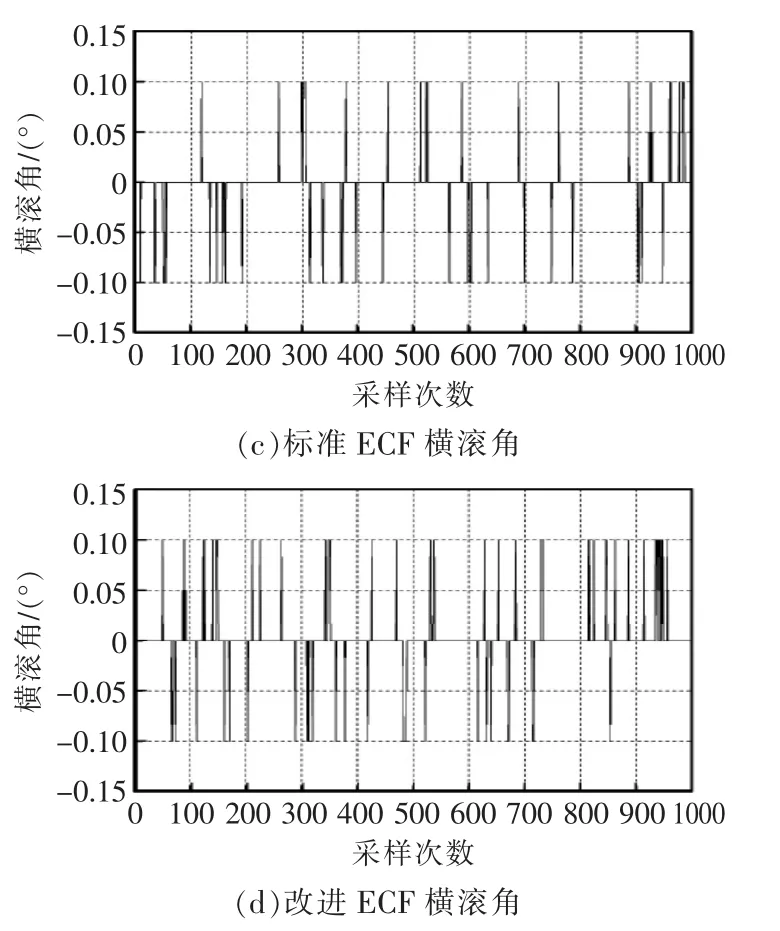
圖6 標準ECF和改進ECF靜態測試Fig.6 Standard ECF and improved ECF static test

表2給出了2種算法姿態角的均方根誤差、最大值及最小值。對比2組數據，可知2種算法在姿態解算的精度上差別不大，說明改進ECF保證了姿態解算的準確性。

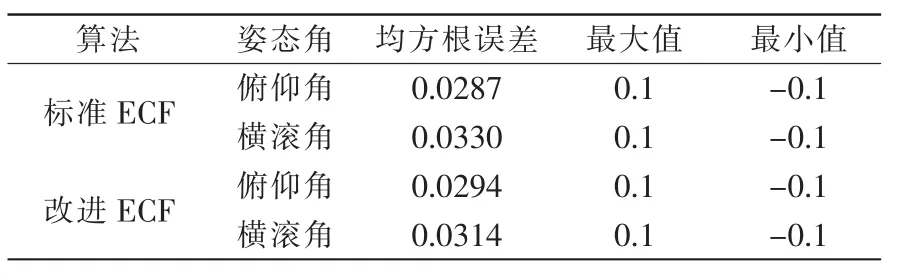
表2 靜態測試下兩種算法姿態解算誤差Tab.2 Attitude estimation errors of two algorithms in static test

將試驗平臺沿Y軸固定在碳纖維桿上，保證四旋翼只能繞單軸運動。使四旋翼以不同角速度做繞軸運動，同時將2種算法解算出的俯仰角發送至上位機進行顯示，姿態采樣時間為4 ms；為了更容易觀察波形，選取發送周期為姿態采樣周期的3倍，如圖7所示共選取了1000個采樣點。

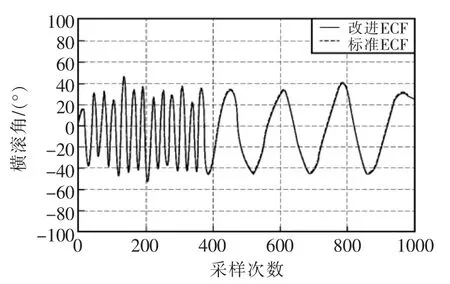
圖7 動態測試姿態的整體對比Fig.7 Overall comparison of dynamic attitude testing

為了更清楚地反映不同角速度下2種算法姿態的效果，進行了局部姿態的對比，如圖8所示。由圖可見，在慢速轉動時，2種算法解算的姿態跟隨幾乎沒有差別；而在快速轉動時，標準ECF相對于改進ECF解算的姿態有明顯的滯后。

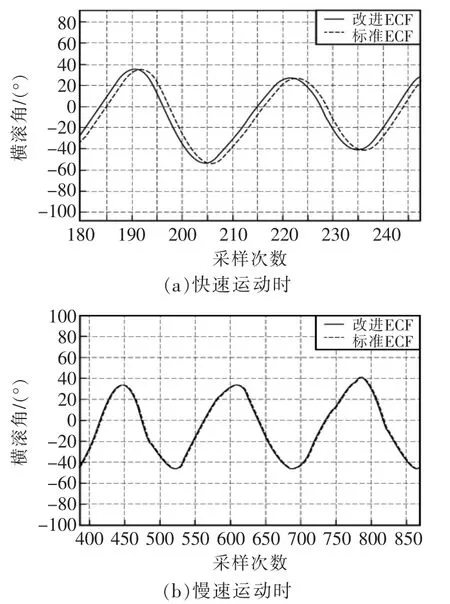
圖8 不同角速度運動的局部姿態對比Fig.8 Local attitude comparison of different angular velocities

為了進一步確定標準ECF相對于改進ECF的滯后時間，分別選取在50，150，250，350采樣點附近進行比較，對比結果見表3。由表可算出平均滯后時間約為24 ms。

通過動態繞軸試驗，說明了改進ECF姿態解算的實時性相對于標準ECF，有了明顯的提高。

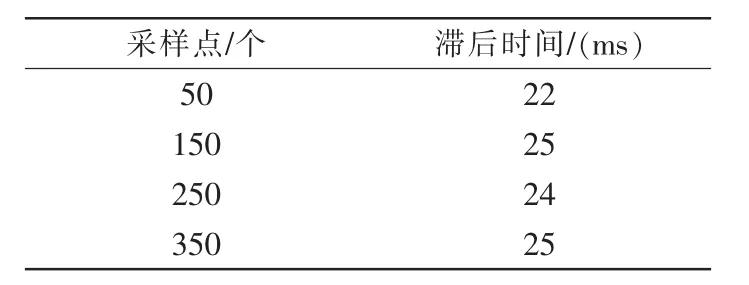
表3 姿態估計滯后時間的對比Tab.3 Comparison of lag time in attitude estimation

6 結語

文中設計了一種改進顯性互補濾波算法，在IMU數據融合之前對加速度原始數據進行巴特沃斯低通濾波，同時設置了緩存區保存更新后的四元數向量，在緩存區中取出與加速度對應時刻的四元數向量進行數據融合，在保證了精確度的基礎上提高了姿態解算的實時性。為了驗證文中所設計算法的有效性和實用性，搭建了四旋翼飛行器試驗測試平臺，將文中所設計的算法與傳統的顯性互補濾波算法在試驗平臺上進行了靜態試驗和動態繞軸試驗。試驗結果表明，該算法能有效地減小加速度白噪聲對姿態解算精度的影響，改善了加速度低通濾波之后造成姿態解算滯后問題，保證了姿態解算的精確度，提高了姿態解算的實時性。