基于PCA—DEA法的銀行效率評價研究

鄭 航，許淑嫻，陳永平

（1.武夷學院 數學與計算機學院，福建 武夷山 354300;2.武夷學院 機電工程學院，福建 武夷山 354300）

隨著中國加入到WTO，中國銀行將面臨更加嚴峻的挑戰，銀行間的競爭集中表現為效率的競爭，如何提高銀行的效率是能否經受考驗的關鍵。國內外對銀行效率評價研究已有很多，對銀行投入和產出效率評價大都采用DEA方法。文獻[1]-[4]使用DEA模型來評價銀行效率問題，采用不同的投入和產出變量，從生產效率的角度來評價銀行效率水平。文獻[5]為區別DEA有效決策單元之間異同，應用了超效率DEA模型。文獻[6]采用超效率DEA模型與Tobit模型結合，利用超效率DEA得分對全部支行進行排序之后，再應用Tobit模型進行了效率影響因素分析，發現存款特點、收入結構、支行類型、區劃分布等因素對支行的運營效率構成了顯著影響。文獻[7]應用AHP-DEA模型，通過AHP法對評判指標構造判斷矩陣從而減少評價者的主觀性，應用DEA方法計算得到客觀數據，以量化的數據指標來判斷商業銀行績效水平。文獻[8]通過因子分析法對全國 13家主要商業銀行 15個績效指標進行分析，得出各家銀行在銀行規模因子、銀行人均效益因子、銀行安全性因子、銀行成長性因子、銀行盈利性因子諸方面的表現，并按照特征值加權給出了各家銀行的績效排序。文獻[9]利用改進因子分析法對反映銀行規模效率的28個指標篩選，得出2008-2013年的主因子，應用熵值法對主因子進行客觀賦權，進而得出每年各大商業銀行的績效評分排名。基于以上學者大多采用DEA法從效率值等角度評價銀行效率，但從投入和產出變量之間的線性相關性，評價指標個數過多等將影響DEA模型的有效評價性的角度，考慮較少。因此本文為遵循DEA方法的拇指法則[10]（即評價對象至少是投入、產出指標變量的兩倍的限制），提高評判的精準性，增加有效單元的區分度，同時也為了解決投入和產出變量之間的線性相關性的問題。采用PCA—DEA方法的組合模型來評價我國銀行效率。

2 PCA/DEA綜合評價模型

2.1 PCA(主成分分析原理）

主成分分析是一種降維的多元統計方法[11]。其特點在于將多指標變量降維成少數幾個相互獨立但包含原變量大部分信息。具體計算步驟：第一步：標準化原始數據X，計算X的相關系數矩陣R；第二步：求R的特征值 λ1≥ λ2≥ λ3≥… ≥ λp≥ 0 及對應的特征向量a1,a2,a3,…,ap；第三步：根據累計方差的貢獻率達到85%，取前m個特征值及相應的特征向量，得到因子載荷陣A=（aij）p×m；第四步：寫出主成分：Fi=a1iX1+a2iX2+… +aniXP，（i=1,2,…p）。

2.2 DEA模型

DEA法是評價具有多投入和多產出的決策單元相對效率的有效方法之一，它的優勢在于不需要建立變量之間的函數關系，有效避免主觀因素，在對產出變量加權求和與投入變量加權求和的比值基礎之上，來測算決策單元的相對效率[12]。DEA法目前使用最多的兩種模型分別是CCR模型和BCC模型。CCR模型如下表示：

上式中Ork為第r個決策單元的k個產出變量,Iij為第i個決策單元的j個投入變量。ark、βik分別為產出與投入變量的權向量。這里滿足0≤hi≤1。當時hi=1,即第i個評價單元位于效率前沿邊界上，是技術有效的狀態。

3 實證分析

3.1 指標體系的建立

選取投入和產出指標借鑒中國銀行競爭力報告[13]對世界各銀行排名時所用的指標，共選取了13個指標來對我國銀行的效率進行分析。能具體體現銀行總體的實力與業務運作能力，銀行的管理能力，銀行整體的規模等的指標作為投入指標，如資產總額、員工數、業務及管理費等；而能反應出銀行的收入狀況，或直接體現出銀行綜合效益水平的指標作為產出指標，如利潤總額、利息凈收入、手續費及傭金凈收入等，具體見表1。

表1 投入與產出指標Table 1 Input and output indicators

3.2 計算過程

本文選擇了中國四大國有銀行：建設銀行（CBC）、農業銀行（ABC）、工商銀行(ICBC)、中國銀行(PBC)；四家代表性的商業銀行：興業銀行(CIB)、民生銀行(CMBC)、交通銀行(BCM)、招商銀行(CMB)，共 8 家銀行作為評價對象，這些評價對象具有同質性。

指標數據來源于2015年的各銀行的年報，由于投入、產出各指標都有不同的量綱，如果直接帶入DEA模型中將降低分析效率，因此將投入和產出指標A1-A7，B1-B6應用spss20.0軟件分別進行歸一化，消除量綱影響。得到A'1-A'7，B'1-B'6，由于表 2，3中投入和產出各指標歸一化得分數據有負值，不滿足模型中投入、產出變量非負性的約束條件，故對上述數據向上平移 2 個單位[14]，見公式（2）。

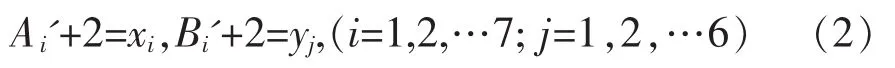
平移后投入和產出分別記為x1,x2,…,x7和y1,y2,…,y6，結果見表 2，3。

將表 2，3 中各投入（x1,x2,… ,x7）和產出（y1,y2,… ,y6）代入到模型（1），應用deap2.1軟件計算得各評價單元的技術效率，計算結果見表4。

由表4可看出技術有效的決策單元為6個，非有效的為2個，區分度低。這是由于評價指標個數過多，會違背拇指法則。因此考慮縮減投入和產出指標個數，故對投入指標和產出指標進行主成分分析，選取代表性主因子。依據主成分分析法步驟對投入指標

（x1,x2,… ,x7）、產出指標（y1,y2,… ,y6）進行歸納綜合。由于投入變量的前兩個主成分的累計方差貢獻率達到，即前兩個主成分包含了7項投入指標的大部分信息，選取前兩個主成分為新的投入變量，分別記為：I1，I2；同理，產出變量的原始兩個主成分的累計方差貢獻率達到，也綜合了原6項產出指標，新的產出變量分別記為：O1、O2。結果見表 5，6。 同時應用 spss軟件得出投入產出各成分載荷矩陣，計算結果見表7。

表2 歸一化后投入變量Table 2 The input variable after normalization

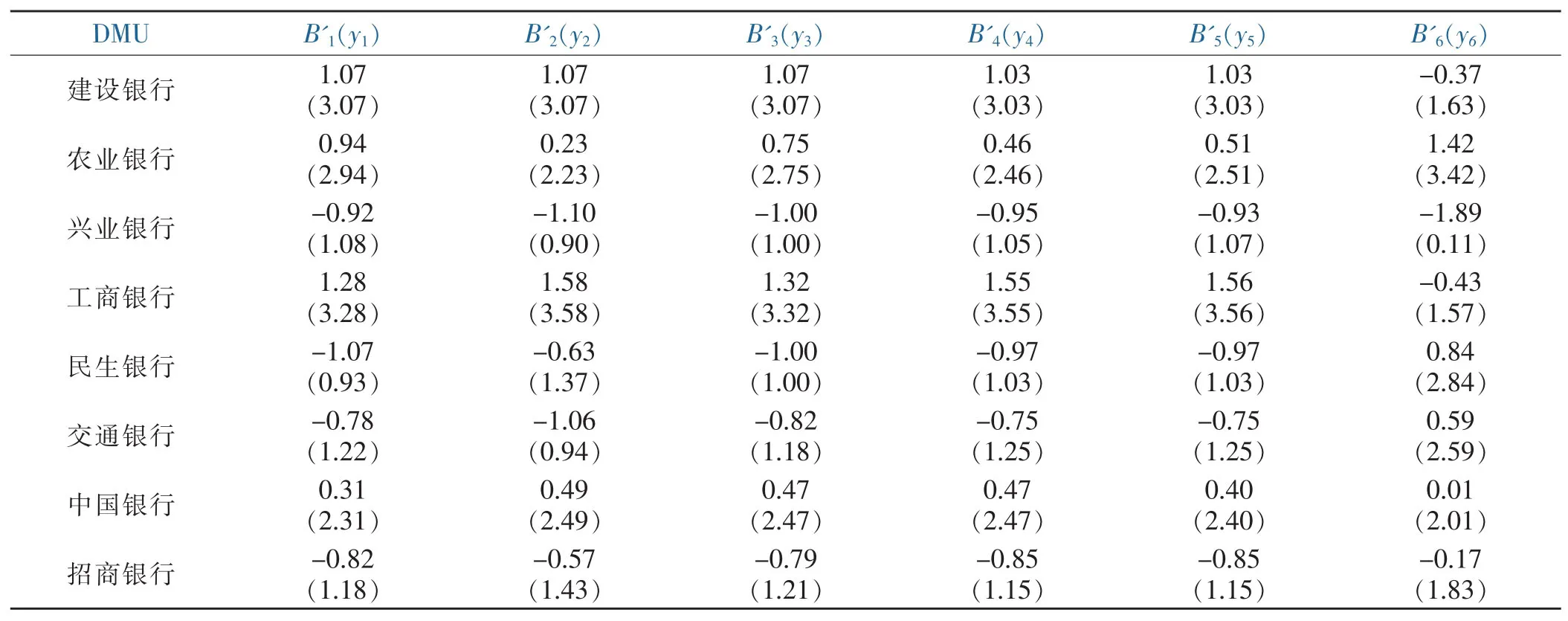
表3 歸一化后產出變量Table 3 Output variable after normalization

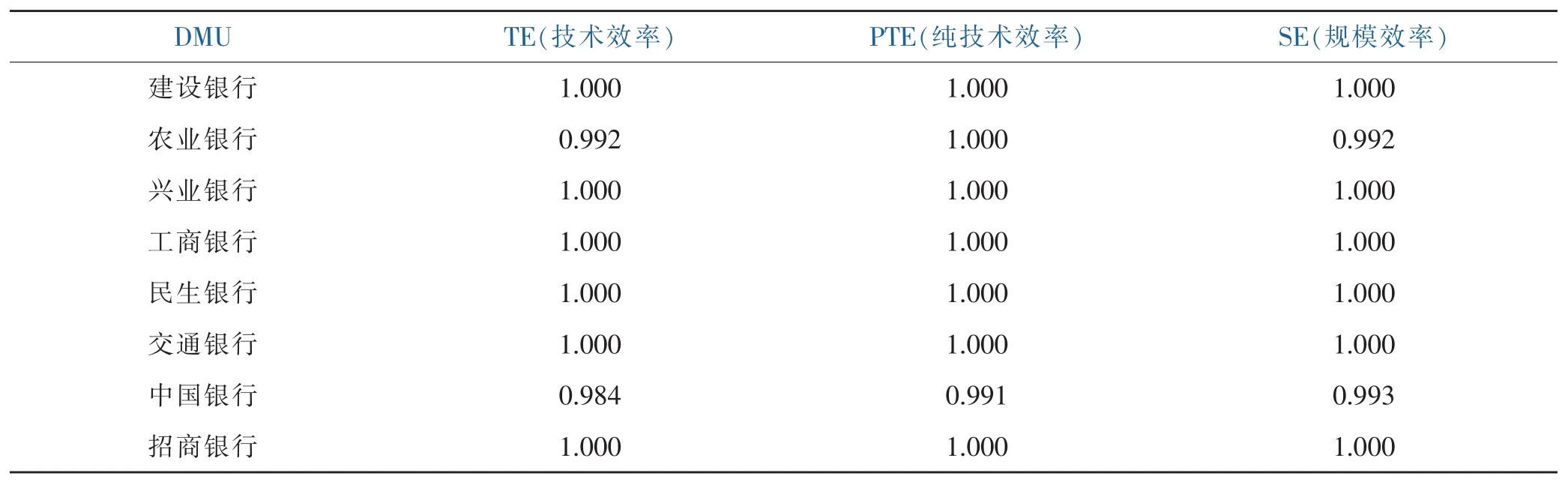
表4 各銀行評價效率Table 4 Banks evaluate efficiency

在投入主成分I1中，資產減值損失、資產總額、業務及管理費等載荷較高，稱為總付出因子。I2中不良貸款率載荷較高，稱為不良貸款率比因子。而在產出主成分O1中利息凈收入、營業收入、利潤總額等載荷較高，稱為總收益因子。O2中成本收入比載荷較高，稱為成本收入比因子。

上式中X1,X2,… ,X7；Y1,Y2,…,Y6為原始投入和產出指標數據，再對I1、I2，O1、O2分別進行歸一化，應用公式（2），再帶入模型（1），使用deap2.1軟件計算評價對象的技術效率、純技術效率、規模效率，具體結果見表8。

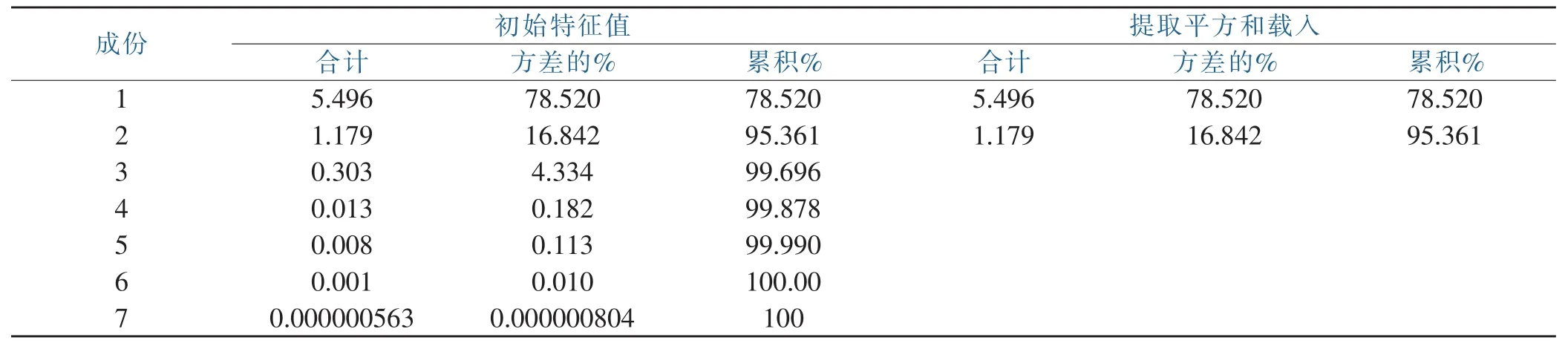
表5 投入解釋的總方差Table 5 Total variance of input interpretation

表6 產出解釋的總方差Table 6 Total variance of output interpretation

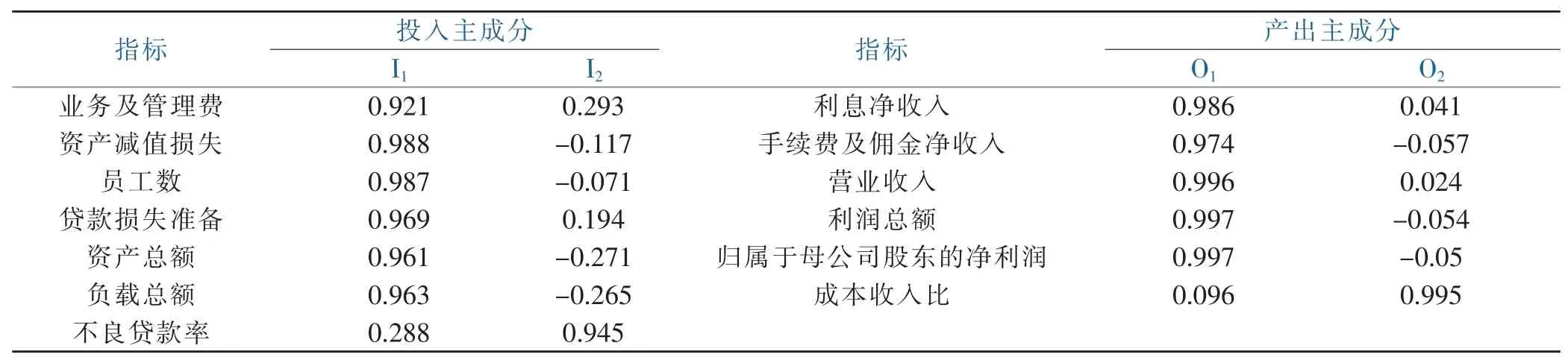
表7 投入產出各成分載荷矩陣Table 7 Input and output load matrix of each component

表8 改進后各銀行評價效率Table 8 The improved efficiency of bank evaluation

4 結果分析

對比表4和表8技術有效的評價單元個數，不難發現，當對投入和產出指標進行主成分篩選后，再結合DEA模型進行效率評價，技術有效的決策單元由原來直接使用DEA法評價的6個，降為4個。而純技術效率和規模效率非有效的評價單元也增多。結果表明PCA與DEA方法相結合組合評價模型在評價銀行效率方面，能提高評判的精準性，體現出一定的區分度。因此該組合評價方法具有一定的理論價值和實用意義，而各非有效的銀行應該采取措施減少資產減值損失、加大業務及管理費的投入，減少不良貸款率，從而達到技術有效。