基于信息熵的物料配送時間節點預測方法

任瑩暉 黃向明 馬忠凱 周志雄

湖南大學機械與運載工程學院,長沙,410082

0 引言

隨著現代制造技術的發展，眾多行業產品同質化嚴重，技術、材料等水平相近，因而通過降低原材料成本以提升企業效益空間已經日漸困難。而通過改善被視為“第二類生產”的企業車間內部生產物流來提升企業效益，已經成為企業發展的一個重要競爭要素[1]。其中車間內部的物料配送是保障生產順利進行的基礎，然而離散型制造企業生產過程中經常存在各種干擾因素，比如設備故障、裝配質量不過關、零部件加工缺陷、裝配工藝變更等。這些干擾因素導致生產節拍不穩定，物料配送時間節點難以精確控制，進而增加了企業生產的時間成本，因此，如何提升企業生產物流的物料配送時間節點的準確性，已經成為眾多企業亟需解決的問題。

目前，國內外學者對如何提升離散型制造企業物料配送時間的準確性展開了研究。葛茂根等[2]提出了以物料運輸成本、運輸時間和線邊庫存為優化目標的多目標準時化物料配送模型。劉明周等[3]構建了一種基于射頻技術的動態準時制物料配送控制系統。沈維蕾等[4]提出了一種基于實時信息驅動的物料配送模式。彭濤等[5]提出了改進免疫克隆選擇調度算法以提升車輛裝配線物料配送的準時性。周炳海等[6]綜合考慮搬運設備的運載能力和裝配線不允許缺貨約束，構建了車輛裝載與路徑規劃的聯合優化模型，以提升混流裝配線物料配送的準時性。EMDE等[7]針對汽車生產線中以物料超市為基礎的小批量循環配送問題進行研究，并給出了配送時間優化算法以減少線邊庫存。HANSON等[8]提出了生產線物料配送的minomi概念，提高了多品種小批量產品生產過程中物料搬運和存儲的效率。

綜上所述，國內外學者從改進物料配送模式、建立實時生產監控系統、優化物料配送路徑等方面研究了提升物料配送時間準確性的方法，而在不確定條件下的物料配送時間節點預測及預測精度控制方面還有待深入研究。本文所考慮的不確定性條件是指在生產過程中存在的導致生產過程發生擾動，但是又可以進行管理和控制的事件。不考慮位于生產過程之外，但是也能引起生產過程發生擾動的事件。不確定條件下的干擾因素往往具有不確定性，對生產過程造成不同程度的擾動。本文面向不確定條件下的復雜產品裝配過程，建立一種基于馬爾可夫鏈特征的物料配送時間節點預測方法，并結合某多品種小批量中小型傳統離散型制造企業生產現狀，對預測方法的有效性進行評價。

1 不確定條件下的裝配過程分析

1.1 干擾因素分析

在復雜產品的裝配生產過程中，干擾因素源自多方面。根據實際生產狀況，本文將從客戶端、裝配生產端、零部件供應端三個方面對干擾因素進行分類，并描述其對生產的影響。

(1)客戶端。來自客戶端的干擾因素主要指客戶的自身需求變化，比如客戶對產品數量、交貨期、質量要求等的變更，導致生產計劃、資源調配、生產工藝等變化。

(2)裝配生產端。來自裝配生產端的干擾因素主要指裝配過程中各種實體要素和非實體要素的狀態、數量的變化，導致裝配工序處理時間、裝配質量等出現不穩定。

(3)零部件供應端。來自零部件供應端的干擾因素指由于原材料、外協件、外購件供應商或生產部門供應端的復雜性，造成提供的部件質量和數量不穩定。

1.2 干擾因素的數字化描述

在實際生產過程中，干擾因素只有發生與不發生兩種狀態是一個定性的事件，各種干擾因素對生產過程的影響程度難以顯性表達。為了更加直觀地描述干擾因素對整個生產過程的影響，文獻[9]采用了時間能力因子ΔTc和時間需求因子ΔTl對干擾因素進行數字化描述，但實際生產過程中的不同時間內，其中一種干擾因素可能會引起另一種干擾因素的出現，不同的干擾因素也可能并行發生，各種干擾因素并非完全相互獨立，因此不能將干擾因素對生產過程的影響程度進行簡單疊加。

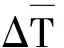
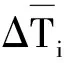
(1)

式中，ΔTij為工位i在j狀態下的綜合時間需求因子，即相比理想狀態下出現的配送時長變化量。

2 配送時間節點預測方法

2.1 裝配工位狀態定義

(2)

式中，Tixs為工位i在第x次采樣時物料實際需求配送時間節點；Tixp為工位i在第x次采樣時物料理想配送時間節點。

根據系統各工位不同狀態出現的時間長短，可以得到各工位不同狀態出現的概率Pij與其綜合時間需求因子ΔTij:

(3)

(4)

x=0,1,2,…m≤n

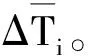
2.2 工位狀態轉移概率矩陣的構建

各種干擾因素的發生與否以一定的概率在不同狀態之間不斷轉移，其變化過程具有隨機性。當已知各種干擾因素當前所處狀態時，其將來的狀態只與現在的狀態有關，與過去所處的狀態沒有關聯，干擾因素具備馬爾可夫性。工位狀態變化是干擾因素狀態變化的直接表現，因此工位的狀態變化同樣具備馬爾可夫性。

在實際裝配作業過程中，裝配工位狀態轉移的時間點是不確定的。需要連續觀測各種干擾因素的狀態，以確定工位所處狀態，同時工位所處不同狀態時間也是連續的。因此，工位狀態變化過程對應的是時間連續狀態離散的馬爾可夫鏈，具有連續時間馬爾可夫鏈的基本性質[10]。馬爾可夫預測模型是通過研究系統的狀態轉移概率來進行預測，因此狀態轉移概率矩陣的確定是馬爾可夫預測模型的關鍵。

在某一事件不斷發展變化的過程中，它從某一初始狀態出發，在接下來某一時刻轉移至另一種狀態的可能性稱之為轉移概率。假設：X={Xn,n=0,1,2,…}，其狀態空間S取為{1,2,…,n}，對于過程中每一個狀態i和j而言，如果存在：P{Xt+1=j|Xt=i}=P{X1=j|X0=i}，t=0,1,2，…，n，則稱其一步轉移概率為穩定轉移概率，用Pij表示。同樣，如果X在時刻n處于i狀態的條件下，經過m步轉移，在(n+m)時刻到達j狀態的條件概率P(Xn+m=j|Xn=i)稱為X的m步轉移概率，記作Pij(n,n+m)。

當一個事件存在n種可能的狀態，其中任意一個狀態轉移至另一個狀態的轉移概率可以用矩陣的形式表示出來，即狀態轉移矩陣：

(5)

2.3 物料配送時間節點預測

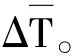
連續型馬爾可夫鏈的C-K方程為

(6)

n,m,k≥0i,j∈S

也可將其改寫為矩陣形式：

P(k+m)(n)=P(k)(n)P(m)(n+k)

(7)

式(6)和式(7)解決了一步轉移概率與k步轉移概率之間的關系。

根據C-K方程可計算得到某裝配工位狀態經過一次轉移之后，即k+1時刻概率分布：

P(1)=P(0)P(1)

(8)

則解決某裝配工位在第k+1裝配過程中可能出現的干擾因素所需時間的期望值為

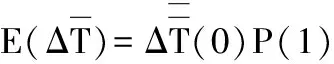
(9)

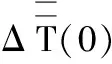
初步預測所得物料配送時間節點為

(10)

式中，Ts為初步預測所得物料配送時間節點；TL為理想狀態下的配送時間節點。

2.4 誤差修正

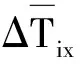
為了避免由此帶來的預測失真，本文提出基于平均預測誤差的動態誤差補償方法。假設在實際預測過程中，相鄰前后兩次預測的誤差具有一定程度的相似性，即用已知的預測誤差來減少當前的預測誤差。同時系統將實時更新歷史數據，并對轉移概率矩陣和初始概率矩陣進行同步更新。具體方法如下。

(1)假設工位i第k次預測配送時間點為tk，實際物料需求時間點為ts，則將物料實際需求時間點與預測所得物料配送時間節點之間的差值稱為第k次裝配的預測誤差，即

Δtk=ts-tk

(11)

式(11)是單步預測誤差，由此可得k步平均預測誤差為

(12)

(2)實際生產過程中出現嚴重意外事件會導致裝配時間大幅增加，同時也會引起極端的預測誤差，這類誤差對正常的預測結果修正沒有參考價值。為了消除這類極端預測誤差，引入預測誤差閾值α，即預測誤差歷史數據的平均值，則式(12)可以表述為

(13)

(3)在實際生產過程中當預測第k+1次配送時間節點時，將多步預測誤差補償至馬爾可夫預測值當中，得到修正之后的第k+1次預測值

(14)

式中，TZ為最終預測所得物料配送時間節點。

前兩項為通過馬爾可夫鏈概率轉移矩陣直接計算得來的配送時間節點，引入了動態誤差補償之后不斷將前面k次的預測誤差補償至下一次的預測結果當中。

3 預測方法評價

預測結果本身會存在誤差，而且這種誤差往往具有累積性。如果一次預測的步長過長，預測結果可能與實際物料需求時間節點產生較大偏差，導致預測失去實際意義。而物料配送時間節點預測準確與否直接影響到生產過程的連續性，因此在實際生產中必須對預測結果進行評價。當發現其預測結果與實際配送存在較大偏差時，必須重新對其預測值進行調整。

3.1 評價指標的選取

物料配送最為重要的就是配送時間的及時性與物料種類和數量的準確性，本文主要研究對象是物料配送時間節點，因此選取配送最大可行性時限Tmax和配送時間節點的準確性為評價指標。其中Tmax指按照某種物料配送方法所制定的配送方案所能夠滿足生產需求的最大時限。該時限越大說明制定配送方案的方法適用性好，反之說明其適用性差。

3.2 基于信息熵的評價方法建立

信息熵是指系統的不確定性，與系統狀態的發生概率有關，目前信息熵理論已在制造系統復雜性和生產系統擾動的研究中得到廣泛應用[11-13]。不確定條件下的物料配送是一個動態變化過程，要建立物料配送系統的評價體系，需要對其復雜度計算并量化評價指標。

系統的復雜度，是指系統難以被理解、描述、預測和控制的狀態，從信息論的角度看，它是指描述該系統的狀態所預期需要的信息量[14]。根據文獻[15]中關于系統復雜度的計算方法，可得配送周期T內且配送精度要求為Δt的配送系統平均靜態復雜度計算公式：

(15)

式中，Pij為工位i處于實際需求狀態j的概率；Si為工位i的計劃狀態數量；M為需要進行物料配送的工位數量。

因配送系統偏離實際需求而產生的平均動態復雜度為

(16)

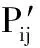
根據式(15)和式(16)可得配送過程中最大有效預測時限Tmax計算公式：

(17)

同樣，配送時間點的準確性可通過整個配送系統中的剩余靜態復雜度[16]來定量描述，即

(18)

通過對配送最大可行性時限和配送準確度的計算，實現了對整個配送系統配送時間節點預測有效性的定量評價。在這一過程中可以通過設置合適的配送可行性時限以控制配送的準確度，同時也可以分析造成偏離的原因，為后續的改善提供依據。

4 實例驗證

以某數控機床生產企業裝配車間為例，驗證并評價本文提出的預測方法。某公司主要生產A型數控磨床，該磨床主要包括磨床上主軸、磨床下主軸、送料盤、箱體、冷卻系統、潤滑系統、動力系統、電氣柜以及外圍輔助部件等，各主要功能部件均設有獨立裝配工位進行裝配作業。該公司采用面向訂單裝配的生產模式，即按照客戶的訂單要求進行生產，包括數量及對產品特殊功能要求。根據歷史訂單記錄2016年1月至6月獲得A型產品訂單180臺，正常情況下采取每天8小時每月22個工作日生產，根據實際情況進行加班作業。根據訂單數量情況，Y公司1月至6月需生產磨床主軸部件360件，理想情況下磨床主軸裝配工位作業節拍為2.67小時。

磨床主軸是該產品的核心零部件，其裝配進度將會影響整個產品的生產周期，因此以磨床主軸裝配工位為例對預測方法進行驗證。按照訂單計劃，每周生產磨床主軸15套，實際作業時間需由理想每周40小時調整為每周60小時(6天，每天10小時)，日配送周期T=10 h。根據實際裝配需求，該工位允許的物料配送時長Δt=1 h。

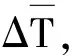
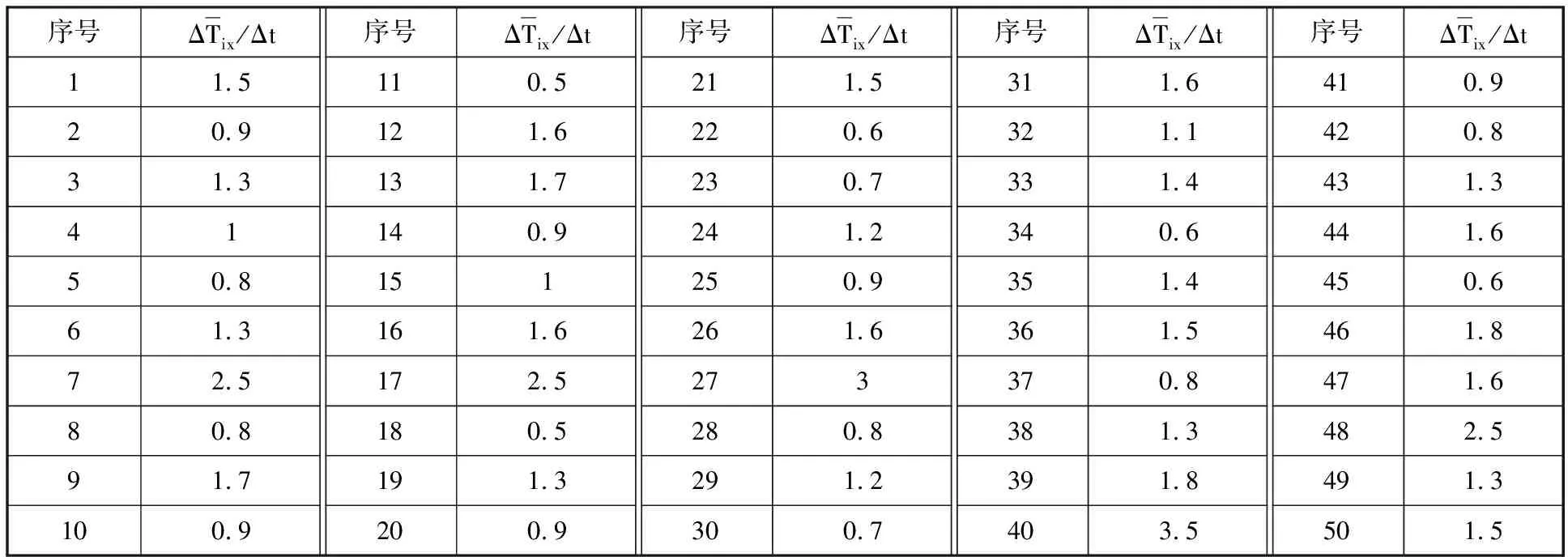
表1 磨床主軸裝配工位采樣值

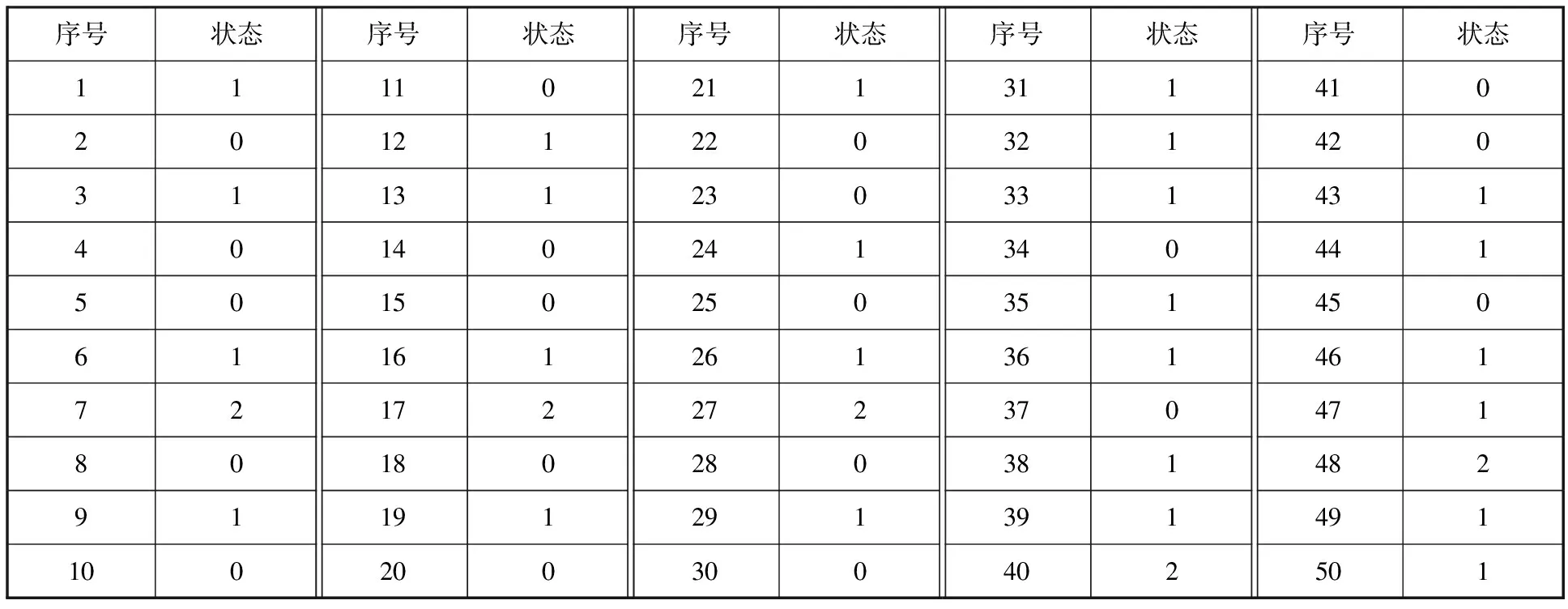
表2 磨床主軸裝配工位狀態

將表1數據代入式(3)和式(4)，可得磨床主軸裝配工位處于不同狀態下對應的平均綜合時間需求與概率分布，見表3。工位狀態隨著干擾因素的發生將會在不同狀態之間進行轉移，表2描述了磨床主軸裝配工位在不同時間內的狀態變化情況。由統計估值法對表2中的工位狀態變化進行計算可得磨床主軸裝配工位狀態的單步轉移概率矩陣：

0 1 2

(19)

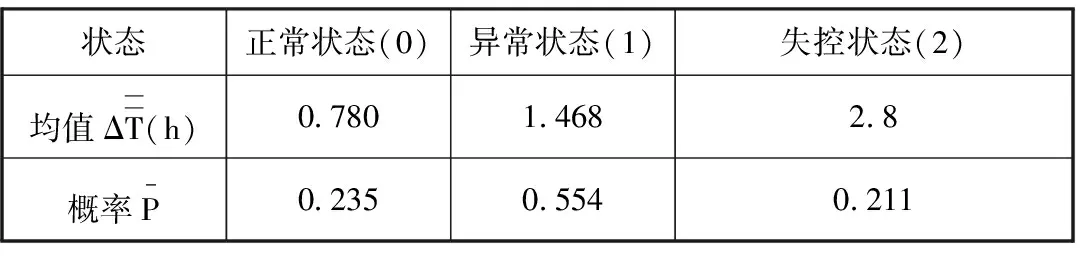
表3 磨床主軸裝配工位綜合時間需求均值與概率

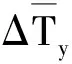
表4 預測值與實測值

表5 經驗配送和預測配送與實際需求差值

為了分析計算磨床主軸裝配工位復雜度，通過觀測磨床主軸工位第X周的實際生產數據(每完成一套磨床主軸部件實際所需時間)，采集15組磨床主軸裝配工位裝配生產節拍Ti，見表6。通過計算每種狀態持續時間長短Ti得到不同狀態出現的概率，即Pi=Ti/(6×10)。根據式(15)得到配送系統靜態狀態描述，見表7。

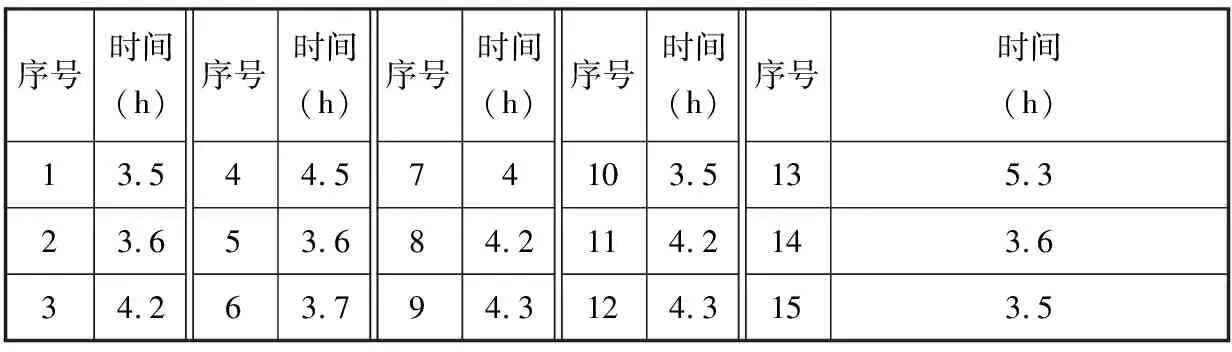
表6 第X周磨床主軸裝配實測生產節拍

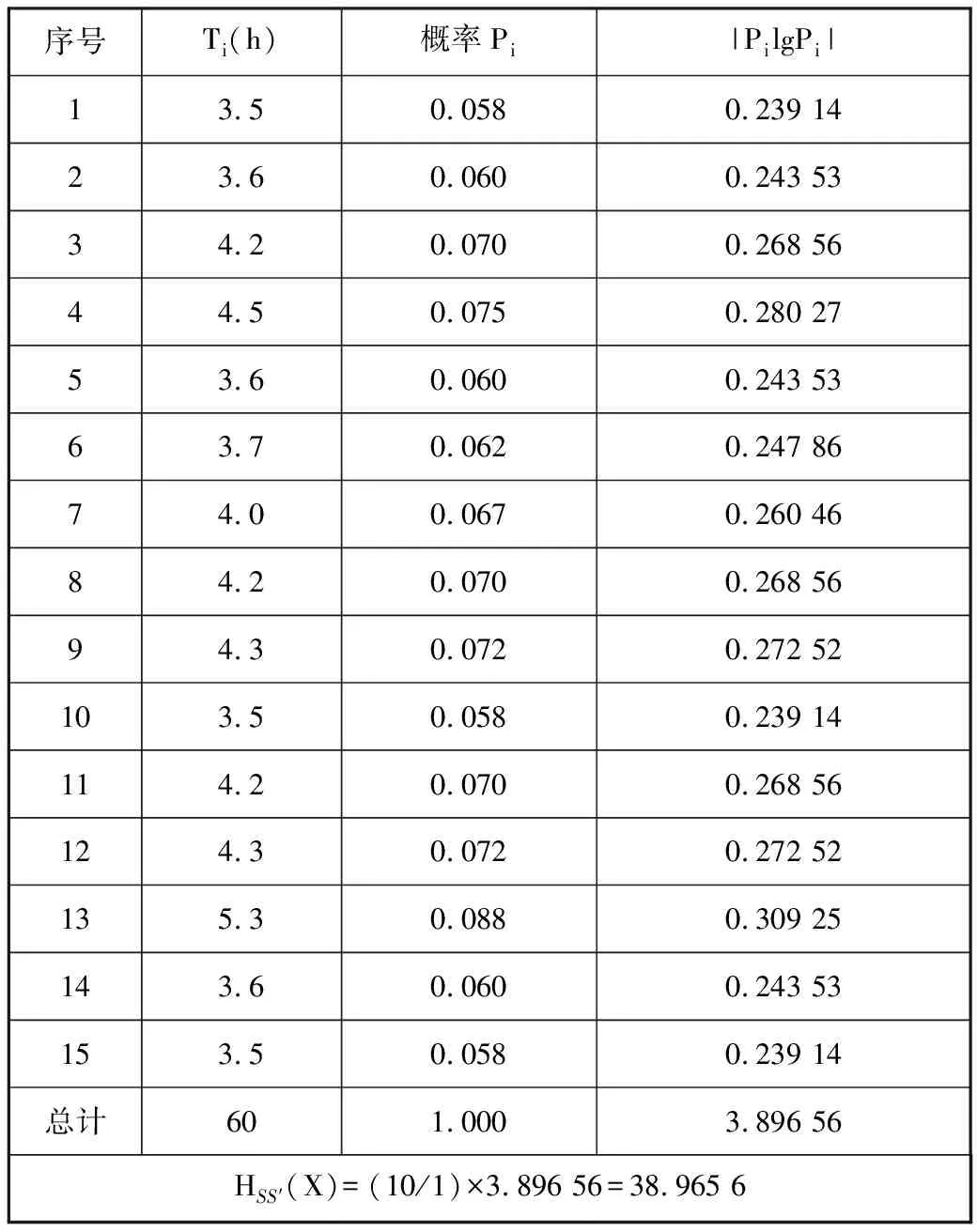
表7 系統靜態復雜度

在實際物料配送過程中，物料的配送時間節點不可能與物料需求時間節點完全吻合，或者提前到達或者延遲到達，這就造成了整個配送系統的波動。通過對實際的觀測，獲得經驗制定的物料配送時間節點、通過預測方法獲得的配送時間節點和物料實際需求時間節點間的差值見表5，根據式(16)可計算得到各自的動態復雜度，見表8和表9。

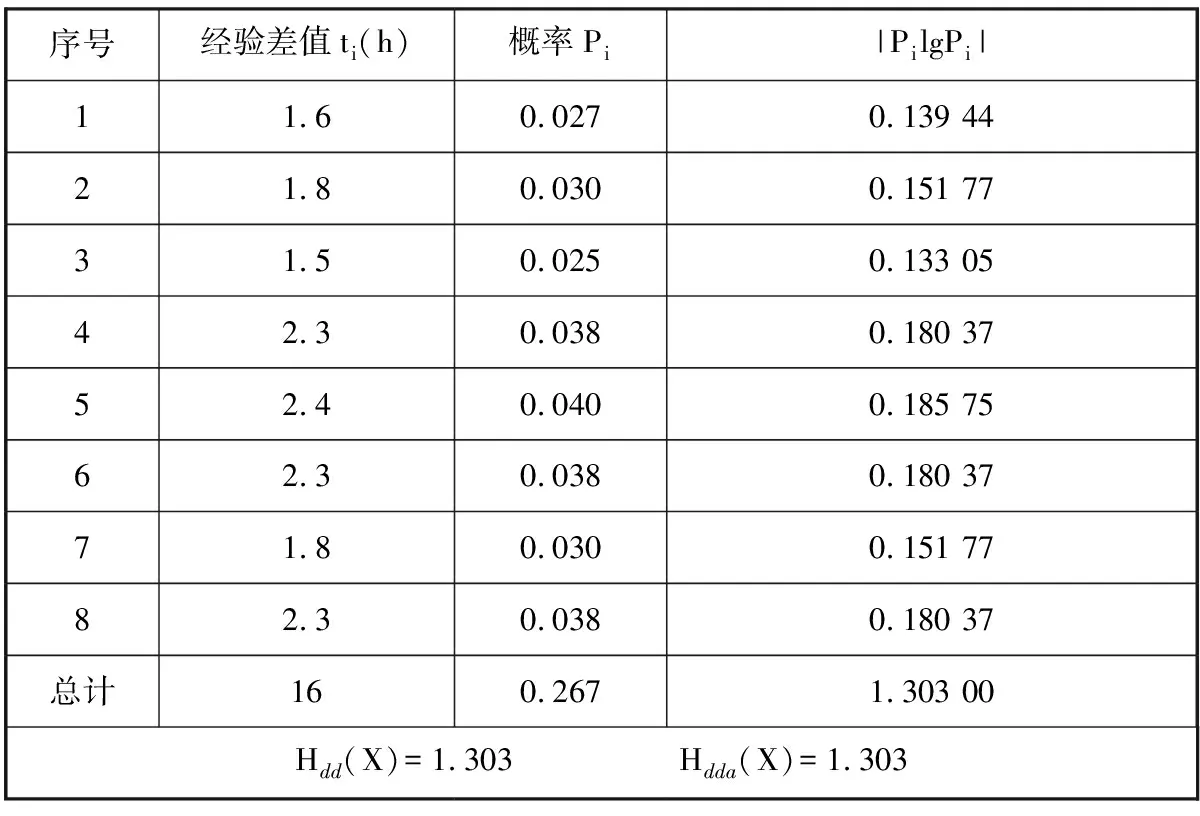
表8 經驗配送與實際需求差值動態復雜度

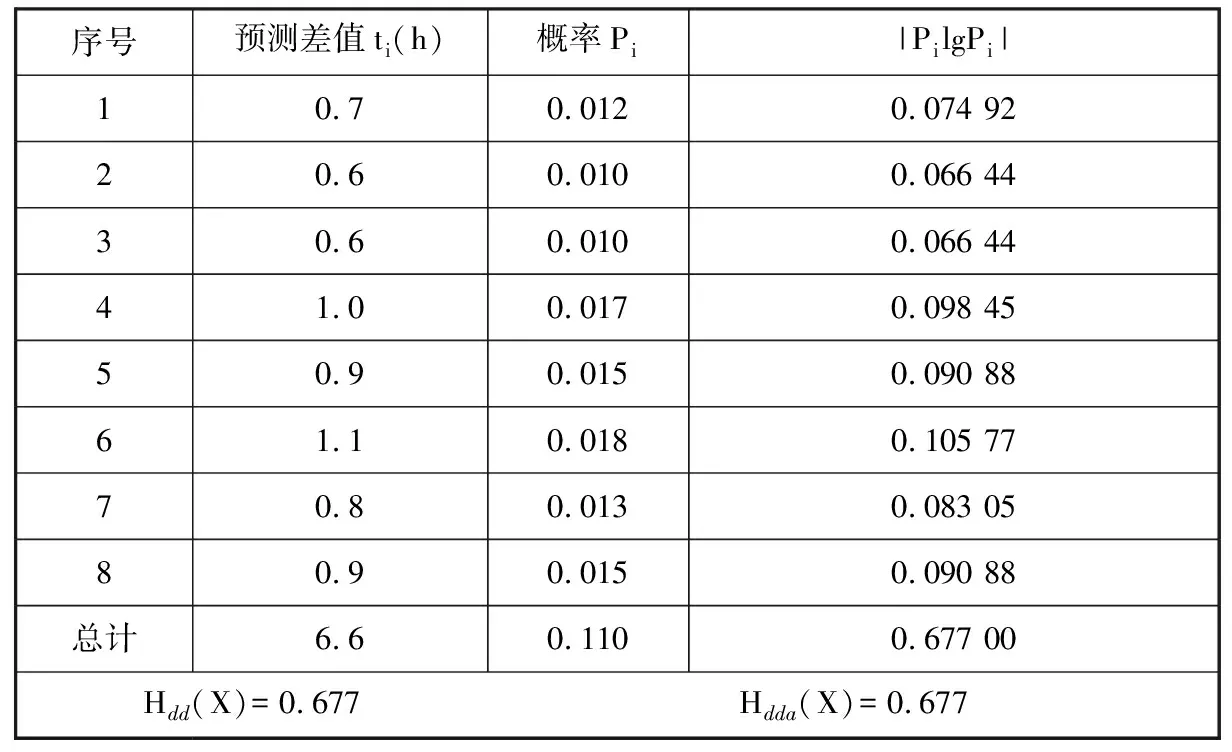
表9 預測配送與實際需求差值動態復雜度

將表8和表9中數據代入式(17)，可分別求得通過經驗配送制定的最大配送可行性時限Tmax1和通過本文預測配送方法制定的最大配送可行性時限Tmax2分別為

上述計算結果顯示，通過經驗配送所制定的物料配送計劃一次最多只能滿足30小時的生產需求。而通過本文預測配送所制定的配送計劃可以滿足近60小時的生產需求。若按照每天工作10小時每周6個工作日計算，預測配送可以制定6個工作日的配送計劃，而經驗配送制定的配送計劃最多僅能滿足3個工作日的需求。

將表8和表9中數據代入式(18)，可分別求得經驗配送和預測配送制定的配送方案準確度分別為

由以上計算結果可見，通過經驗配送所制定的配送方案A1只有66.6%與實際需求吻合，剩下的33.4%由于整個裝配過程的干擾因素而失效。而通過預測配送所制定的配送方案A2中82.6%與實際需求吻合，只有18.4%由于干擾因素而失效。

綜上所述，通過預測配送方案在最大配送可行性時限和配送方案的準確度兩方面都明顯優于經驗配送方案，驗證了本文提出的預測方法的有效性。

5 結論

(1)由于不確定因素干擾復雜裝配車間物料配送時間的準時性，量化干擾因素和工位狀態有助于基于工位狀態變化的馬爾可夫鏈特性預測物料配送時間節點。

(2)提出采用平均預測誤差的動態補償方法，修正了本文提出的物料配送時間節點預測方法的預測精度。

(3)以某數控機床生產企業磨床主軸裝配車間歷史生產數據為例，選取最大配送可行性時限和配送準確度為指標，構建基于信息熵的物料配送系統評價體系。實例研究驗證了本文提出的物料配送時間節點預測方法的有效性。

(4) 本文研究成果對于中小型傳統離散型制造企業，在面對不確定干擾因素影響復雜產品裝配車間物料配送時間準確性問題時，對于提升物料配送時間節點預測的準確性研究和實踐具有一定理論和工程應用指導意義。