自升式平臺弦桿水動力系數的影響因素

田曉潔， 劉運祥， 劉貴杰， 謝迎春， 高志明

(中國海洋大學 工程學院， 山東 青島 266100)

0 引 言

自升式海洋平臺工作環境復雜，波流載荷是平臺所承受的主要載荷之一[1]。自升式平臺樁腿結構比較復雜，通常由細長的桿件組成。在工程中最常用的波流載荷計算方法是莫里森方程，主要由拖曳力和慣性力兩部分組成。利用該方程求解波流載荷的關鍵是確定合適的水動力系數(拖曳力系數Cd和慣性力系數CM)。

為確定Morison公式中的水動力系數，國內外學者做了大量實驗研究。Sarpkaya等[2]對Cd和CM進行大量系統的實驗研究，得到了Cd和CM與雷諾數Re和KC數的關系；任佐皋[3]通過水流-波浪槽實驗得出波流場中的Cd值介于純波動與穩流中的Cd值之間。Yuan[4]進行了靜水和規則波作用于緩慢涌動的垂直圓柱模型的水動力實驗研究。Lupieri等[5]通過實驗分析了圓柱體模型在低KC數的情況下具有規則的波狀流，且入射波峰平行于柱體。Bonakdar等[6]提出了M5模型樹和遺傳算法混合模型來求解水動力系數。Li等[7]對垂直于海床運動的管道進行水動力實驗研究。高暢[8]對自升式海洋平臺樁腿進行海流載荷和波浪載荷的實驗并求出拖曳水動力系數。李少華[1]對海洋平臺水動力系數的反演方法進行了研究。秦文龍[9]計算了南海北部灣處自升式平臺在具體環境下的拖曳水動力系數。國內外學者對于水動力系數的取值已經得到了一些規律性的結論，并且為不同尺寸的樁柱結構物的計算提供經驗值。但是，這些水動力系數的取值使得波流載荷的計算結果偏于保守，與平臺實際環境中的波流載荷差別較大，不利于后續結構的優化設計、動力響應分析，以及對整體結構物的穩定性的分析[10]。因此，確定莫里森方程中拖曳力系數和慣性力系數的取值具有重要的研究意義。

目前關于自升式平臺樁腿的水動力系數的實驗研究，均是基于相似理論進行水池試驗，在實驗過程中的模型縮尺比、波流的入射角度以及樁腿上的齒條等因素對水動力系數的影響均沒有考慮。本文選取樁腿的單弦桿作為研究對象，通過實驗研究物模縮尺比、入射角度以及齒條對水動力系數的影響規律；并且通過多元線性方程，對水動力系數進行修正，為自升式平臺樁腿結構物提供準確的水動力系數。

1 實驗裝置與方法

1.1 實驗裝置

本次單弦桿水動力實驗在中國海洋大學海洋工程重點實驗室的波浪水槽中進行，如圖1所示。波浪水槽長30 m，寬3 m，高1.5 m，水槽兩端裝有大功率水泵用于模擬海流，最高流速為0.5 m/s；另造波裝置可制造最大波高為20 cm，周期為1～2 s的波浪。

根據實驗室的條件，結合單弦桿的幾何特征，搭建了實驗平臺，其原理如圖2所示。在實驗水槽的頂部安裝工裝用于固定整套實驗裝置。在工裝架下依次安裝六維力傳感器、金屬連接盤、法蘭盤以及弦桿模型。在波流載荷作用下，通過六維力傳感器能測得弦桿所受的波流力，將測量的波流載荷轉換為電信號傳輸給DH5902采集儀進行信號的采集與分析。同時在水槽中安裝有波高儀位和流速儀，用于實時測量流速和波高參數。

(a) 實驗水槽(b) 實驗對象

圖1 實驗水槽及實驗對象

圖2 實驗平臺示意圖

1.2 實驗模型設計

考慮到自升式海洋平臺單弦桿的模型縮尺比、波流的入射角以及齒條等因素的影響，設計不同組合的實驗物模進行實驗研究。為研究縮尺比對水動力系數的影響，將物模的縮尺比設計為1∶1、1∶2、1∶5、1∶10；同時設計光滑單弦桿物模和帶齒單弦桿物模。根據實際自升式平臺單弦桿的尺寸，采用幾何相似的原理，設計不同尺寸的實驗物模，具體尺寸和參數如表1所示。

表1 實驗物模參數表 mm

為避免模型本身重力對實驗結果造成影響，同時便于物模的更換，選擇比較輕質的材料，本次實驗選用有機玻璃管作為實驗物模材料。當波流參數較大時，為避免模型在實驗過程中損壞，前期采用ABQUES對有機玻璃模型進行極限實驗工況下的模擬仿真，結果顯示有機玻璃滿足實驗強度要求。在制作物模時頂端和底端都要做好密封處理，防止內部進水；頂端端面打孔與上部的測試儀器連接，實驗物模如圖3所示。

1.3 實驗安排

水動力實驗分為海流實驗組和海浪實驗組，為保證實驗的有效性，設計5組海流參數、5組波浪參數和4組入射角度，具體參數如表2所示。根據圖2搭建的單弦桿實驗平臺，設置波流水槽內水深為1.2 m，依次安裝不同特征的單弦桿，分別模擬不同參數的海流、海浪實驗工況。在進行帶齒條弦桿的實驗時，需要考慮波流入射角度對水動力系數的影響，設置了4種不同角度，具體如圖4所示。每組實驗至少進行3次，以保證實驗數據的有效性與可靠性。

(a) 光滑單弦桿模型

(b) 帶齒單弦桿模型

表2 水動力實驗參數表

圖4 實驗物模裝配及波流入射角

2 分析方法

2.1 實驗結果分析

考慮到實驗組數較多，數據量龐大，僅以1∶2光滑單弦桿的實驗數據為例來說明數據處理的過程，如圖5所示。六維力傳感器能夠采集模型3個維度上所受的實驗力載荷和彎矩載荷，在此為了使采集的主要數據顯示的更加清晰，故不將實驗中的彎矩載荷數據顯示，同時圖中顯示的數據均是截取海流載荷相對穩定時的采集數值[11]。由圖5可以看出，水平力Fx值相對平穩，故可以取此時間段載荷平均值作為該工況下的海流載荷值；弦桿物模在垂直于池壁方向上是不受載荷的，故Fy=0；對于當單弦桿物模在豎直方向上時一方面由于重力與浮力的相互作用而受力，另一方面單弦桿物模同時會受到海流對其的升力作用，所以單弦桿物模在豎直方向上的受力Fz不等于0；而本次實驗只分析實驗模型在波流傳播方向上的受力載荷，故對Fz不予考慮。

圖5 海流實驗數據采集圖

基于Morison方程，根據

(1)

結合實驗工況下的波流力可以推出Cd。根據

(2)

2.2 回歸分析法

針對現有的實驗因素以及實驗結果，結合SPSS軟件中提供的回歸分析方法，采用回歸分析模型進行回歸分析，定量描述水動力系數與影響因素之間的關系。回歸分析[13]是用于確定兩種或兩種以上變量間相互依賴的定量關系的統計方法，能夠反映統計變量之間的數量變化規律，是研究者精準的掌握自變量對因變量的影響程度和方向的有效方法。其線性回歸的數學模型如下所示：

yi=αi+βi1χi1+βi2χi2+…+βikχik+ζi

(3)

式中：α、βik為待估參數；ξ為隨機誤差項；χik為解釋變量。

被解釋變量的變化可以由組成的線性部分α+Xβ和隨機誤差項ξ兩部分解釋。但是得到的線性回歸方程不能立即用于對實際問題的分析，必須對得出的回歸方程進行相關的統計檢驗，包括回歸方程的擬合優度檢驗、回歸方程的顯著性檢驗、回歸系數的顯著性檢驗、殘差分析等。

3 結果分析與討論

3.1 影響因素分析

3.1.1物模縮尺比的影響

圖6為弦桿在各海流速度下，縮尺比與Cd的關系曲線。從圖中可以看出，Cd的取值在0.72～1.12之間；隨著縮尺比的減小，Cd值不斷減小；對于同一個實驗模型，Cd隨流速的增大而增大，當流速大于0.2 m/s時，Cd取值趨于穩定，且各縮尺比的Cd值變化趨勢大體一致。不同縮尺比的Cd值仍在一定范圍內，取值范圍隨縮尺比的增大而整體下移。根據雷諾數公式，雷諾數隨著弦桿直徑的減小而減小，從而驗證了Cd隨雷諾數Re的減小而呈減小趨勢[14]。

圖6 單弦桿縮尺比與Cd關系曲線圖

圖7為CM與縮尺比的關系，可以看出，CM的取值范圍約在1.7～2.05，CM整體上隨縮尺比的減小而增大。這是由于隨著弦桿直徑的減小，KC數逐漸增大，符合CM隨著KC數的增大而逐漸增大的趨勢[15]。

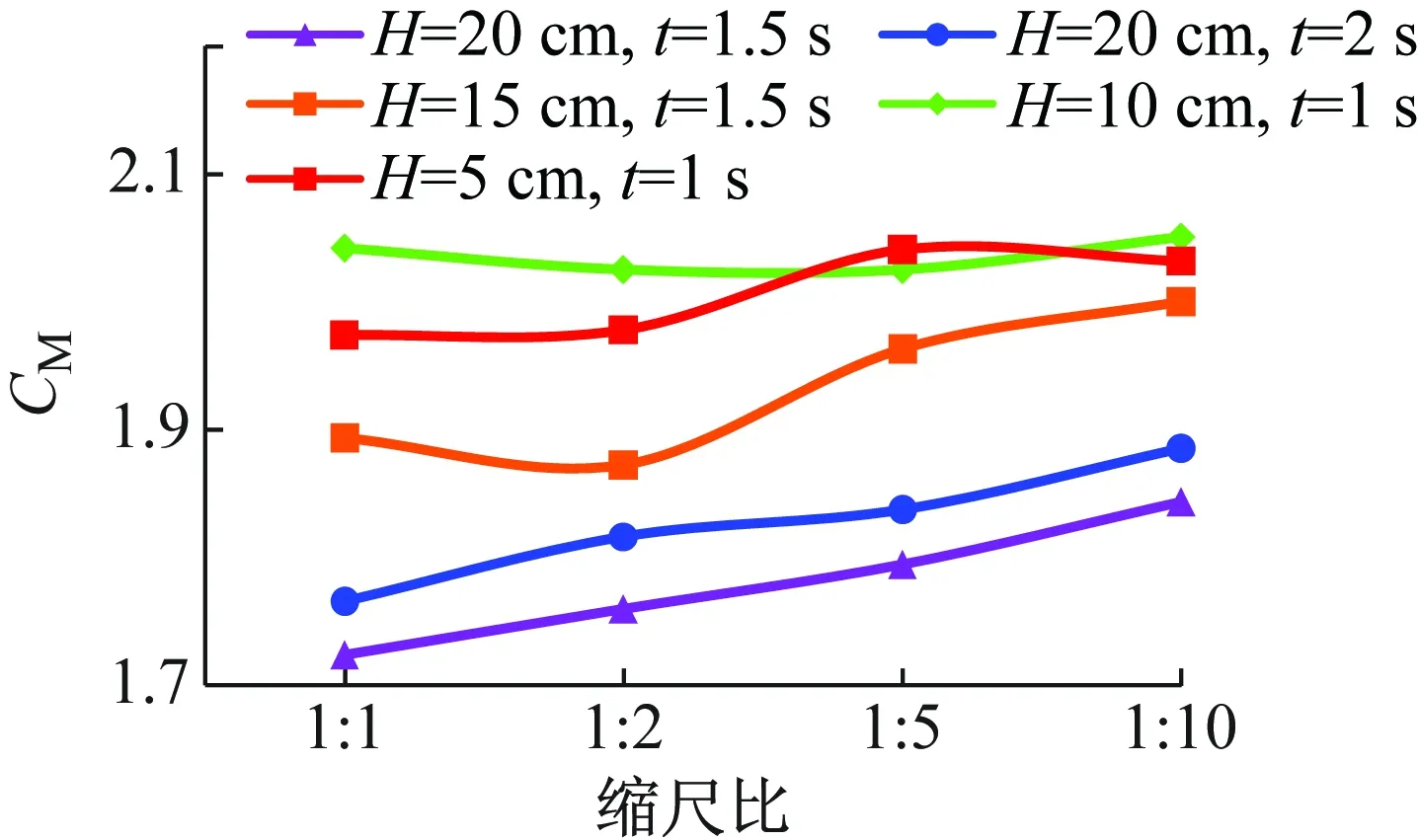
圖7 單弦桿縮尺比與CM關系曲線圖

3.1.2齒條的影響

圖8為在1∶1的實驗模型條件下，齒條因素與Cd的關系曲線，帶齒弦桿的Cd值在1.8～2.2，光滑弦桿的Cd值在0.7～1.2。說明在相同工況下，Cd值的變化與模型的投影面積及模型在垂直于流速方向上的模型形狀具有很大關系,齒條的存在明顯使Cd值增大，相應的物模所受的海流載荷變大。

圖8 齒條因素與Cd關系曲線圖

圖9為1∶1弦桿有、無齒條與CM的關系，帶齒弦桿的CM值相對于光滑桿件的變化較小。說明在相同的工況下CM值受模型的投影面積及模型在垂直于流速方向上的模型形狀影響較小。

圖9 齒條因素與CM關系曲線圖

3.1.3齒條入射角的影響

圖10為不同流速下1∶1帶齒弦桿模型入射角度與Cd的關系曲線。從圖中可以看出，帶齒弦桿的Cd值隨入射角的增大而減小，0°、30°、45°、90°的取值分別在1.9～2.2、1.4～1.7、1.2～1.4左右。這是因為當齒條位于物模正投影區域內部時，齒條對Cd值的影響較小且呈微弱減小趨勢；當齒條位于物模正投影區域外部時，齒條對于Cd值具有明顯的影響，且隨著齒條正投影面積的增加其影響作用加大。

圖10 入射角與Cd關系曲線圖

圖11為1∶1帶齒弦桿不同入射角度與CM的關系，可以看出，CM值隨入射角度的增大而微弱減小，各角度下的CM值在一定范圍內微小波動。由式(2)可以看出，波浪載荷由拖曳力和慣性力兩部分組成，其中投影面積只影響拖曳力部分，而不會影響慣性力。因此投影面積的大小對波浪載荷的影響較小。

3.2 基于線性回歸的數據分析

以弦桿模型有無齒條、模型縮尺比、波流入射角度3個影響因素為自變量，以水動力系數Cd、CM為因變量進行線性回歸分析。經檢驗得出水動力系數Cd、CM與模型齒條、縮尺比、入水角度的多元線性回歸方程為：

圖11 入射角與CM關系曲線圖

Cd=0.905+0.81m+0.131n-0.017q+

0.212mn-0.003nq+8.092×10-5q2

(5)

CM=1.998+0.089-0.225n-0.001q+

0.026mn-0.001nq+0.145n2+

9.315×10-6q2

(6)

式中：m表示有無齒條，取值為0或1；n表示縮尺比，取值范圍為0～1；q表示波流入射角度。

為檢驗該方程的有效性，將實驗測得的Cd、CM值與回歸方程值進行比較，分析其差值并作圖，如圖12和13所示。

圖12 Cd回歸值與實驗值差值結果

圖13 CM回歸值與實驗值差值結果

由圖12和13可以看出，回歸值與實驗值的差值大多數分布在3%～4%以內，其中Cd最大差值是7.52%，CM最大差值是3.41%。誤差比值整體可以接受，表明擬合的方程式能夠客觀地描述水動力系數Cd、CM與模型齒條、縮尺比、入水角度的關系，這在一定程度上為后續水動力系數的研究以及平臺的設計制造提供了參考和數據支撐。

4 結 語

本文針對自升式海洋平臺弦桿的水動力影響因素，通過在實驗水池內搭建測試平臺分別研究縮尺比、入水角度以及齒條對Cd和CM的影響，并通過回歸的方法進行了實驗數據的處理，定量描述水動力系數與模型齒條、縮尺比、入水角度之間的關系。本文的研究工作可為數據處理、傳感器技術、軟件技術和流體力學等方面提供本科教學和大學生科研創新訓練，較好的應用到實踐教學中去。