多過程問題的解答“三步法”

陸永華

多過程問題是機械能及其守恒定律綜合應用問題中的考查熱點之一.由于“多過程”問題涉及的物體運動過程較為復雜，解題能力相對要求較高，對學生而言也是考查的重難點，在此，將多過程問題的解題策略分解為“三步法”：“合”——“分”——“合”：

1.“合”——整體性：通過審題大概了解運動全過程，構建大致的運動圖景，選擇合適的研究過程簡化問題.

2.“分”——階段性+規律性：將全過程進行分解，分析每個過程的規律，其中多過程組合的問題主要是指直線運動、平拋運動和豎直平面內圓周運動的組合問題.常采用的解決方法包括：（1）動力學方法觀點：牛頓運動定律、運動學基本規律;（2）能量觀點：動能定理、機械能守恒定律、能量守恒定律.當涉及重力、大小恒定的阻力或摩擦力做功時，要注意運用它們的功能特點：（1）重力的功取決于物體的初、末位置，與路徑無關;（2）大小恒定的阻力或摩擦力的功等于力的大小與路程的乘積.

3.“合”——聯系性：尋找多過程問題中各個“子過程”之間的聯系，兩個相鄰過程連接點的速度是聯系兩過程的紐帶，也是解題的關鍵，例如平拋運動的末速度的方向是解題的重要突破口.

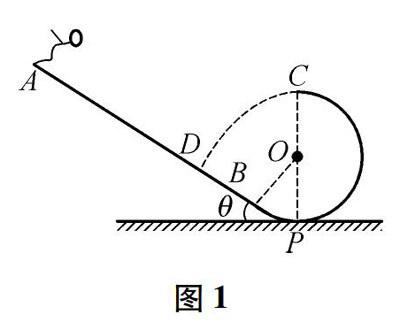
例1 如圖1所示，設一個質量m=50 kg的跳臺花樣滑雪運動員（可看成質點），從靜止開始沿斜面雪道從A點滑下，沿切線從B點進入半徑R=15 m的光滑豎直平面圓軌道BPC，通過軌道最高點C水平飛出，經t=2 s落到斜面雪道上的D點，其速度方向與斜面垂直，斜面與水平面的夾角θ= 37°，運動員與雪道之間的動摩擦因數μ=0.075，不計空氣阻力，當地的重力加速度g取10 m/s²， sin 37°=0.60，cos 37°=0.80.試求：

（1）運動員運動到C點時的速度大小v_C;

（2）運動員在圓軌道最低點P受到軌道支持力的大小F_N;

（3）A點距過P點的水平地面的高度h.

分析：第一步的“合”，確定本題中的運動圖景為直線運動、圓周運動和平拋運動的組合運動過程.第二步的“分”，將整個過程分為直線運動、圓周運動、平拋運動三個子過程，結合題目中的（1）（2）（3）問中求解的物理量進行分析，第（1）問運用平拋運動的規律;第（2）問關鍵是運用能量觀點分析圓周運動，求解出 P點的速度;第（3）問運用能量觀點分析A到P過程求解高度h.其中在求解這三問的過程中，第三步的“合”已體現其中，如銜接點P點和C點的速度.具體求解過程如下：

例2 如圖2所示，光滑水平面AB與豎直面內的半圓形導軌在B點相切，半圓形導軌的半徑為R.一個質量為m的物體將彈簧壓縮至A點后由靜止釋放，在彈力作用下物體獲得一向右的速度后脫離彈簧，當它經過B點進入導軌的瞬間對軌道的壓力為其重力的8倍，之后向上運動恰能到達最高點C，C、O、B三點在同一豎直線上.（不計空氣阻力）試求：

（1）物體在A點時彈簧的彈性勢能;

（2）物體從B點運動至C點的過程中產生的內能.

分析：第一步的“合”，確定本題中的運動圖景為直線運動和豎直平面圓周運動的組合運動過程.第二步的“分”，將整個過程分為直線運動和豎直平面網周運動兩個子過程，其中第一個直線運動過程包含在彈簧彈力作用下的運動，求解彈簧的彈性勢能沒有直接的公式可以代人，常規思路是根據能量守恒定律進行求解，第二個子過程求解物體從B點運動至C點的過程中物體做豎直平面網周運動所產生的內能，這個內能的產生來源于摩擦力做功，但是在此沒法直接運用摩擦力做功公式代人求解，同樣需從能量守恒定律角度進行求解.

第三步的“合”主要體現在兩個子過程的銜接點B點速度.具體求解過程如下：

學會并熟練分解多過程問題，進行三步式的分析解答，結合動力學方法觀點和能量觀點進行求解，多過程問題便可迎刃而解.