煤礦斜井連續帶式出渣機軟起動方式優化研究

蔣永春， 管會生， 陳 明， 曾文宇

(西南交通大學機械工程學院， 四川 成都 610031)

0 引言

目前煤炭主導著我國能源市場[1-2]，保持煤炭的穩定開采至關重要。近年來，盾構法已成為隧道施工的一種主流方法[3]，而斜井煤礦隧道盾構施工需要長距離、大運量、大功率且具有高可靠性的連續帶式出渣機。長距離斜坡連續帶式出渣機的起動設計是一個難題，其起動時輸送帶各點的速度、加速度、張力和系統驅動力是設計中的關鍵參數，它們會直接影響連續帶式出渣機的使用壽命。傳統設計方法已經很難滿足設計要求，為降低成本，得到可靠且高效的連續帶式出渣機，需要改進設計方法，并探究最佳起動方式。

目前，國內學者對于連續帶式出渣機的動態特性開展了一定的研究。徐靜等[4]建立了基于集中質量的有限元方法的皮帶輸送機的動力學模型，研究了皮帶輸送機的縱向動態特性；劉肖健等[5]在皮帶輸送機的計算機輔助設計中采用了動態仿真技術，得到了不同配置參數下的輸送機動態特性；管會生等[6]針對鉆爆法施工連續帶式出渣機的起動階段進行了動態特性研究，基于正弦加速度起動曲線的動態仿真得到了優于傳統設計方法的設計參數。

以往研究多集中于水平連續帶式出渣機的研究，針對斜井隧道所用連續帶式出渣機的研究甚少，尤其在只有1臺盾構在掘的煤礦斜井隧道中，出渣距離長，系統受力情況更為復雜，且在重力做功的情況下其動態特性會有所不同。本文以神華新街煤礦斜井盾構施工所用連續帶式出渣機為研究對象，研究該連續帶式出渣機的動態特性，以其起動時的關鍵參數最優化為目標，建立動力學模型，通過動態仿真和比較采用不同的起動加速度曲線的軟起動方式，探究最佳起動方式，獲得最優設計參數。

1 動力學模型建立

1.1 工程概況

該連續帶式出渣機用于神華新街煤礦斜井盾構施工。斜井隧道長度超過6 500 m，坡度為6°。針對該工程，采用常規設計方法計算得到連續帶式出渣機主要參數見表1。

表1 連續帶式出渣機常規設計主要參數[7]

連續帶式出渣機主要結構有主驅動、皮帶硫化機、中間驅動、皮帶延伸裝置、儲帶張緊裝置及后配套拖車等。中間驅動可增強帶式運輸系統的動力，解決帶式運輸機因運輸距離過長而引起的動力不足的問題。儲帶張緊裝置負責放帶和張緊輸送帶。圖1為該連續帶式出渣機示意圖。

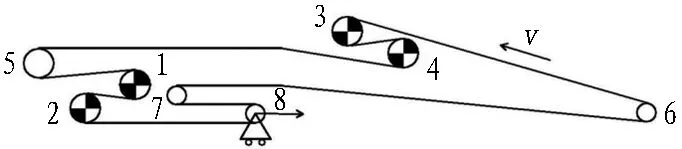
1—機頭第1驅動； 2—機頭第2驅動； 3—中間第1驅動； 4—中間第2驅動； 5—機頭改向滾筒； 6—尾部改向滾筒； 7—張緊改向滾筒； 8—張緊滾筒及張緊小車。

圖1連續帶式出渣機示意圖

Fig. 1 Sketch of continuous belt conveyor

1.2 離散動力學模型建立

輸送帶材料本身具有蠕變性、滯后性以及松弛特性，且應力與應變具有非線性關系。Kelvin模型[8]的結構同樣具有蠕變性，雖然不具備松弛特性，但是該長距離帶式出渣機系統中設有張緊裝置，可以補償輸送帶的松弛特性。因此，選用Kelvin模型建立連續帶式出渣機的動態模型。

連續帶式出渣機結構復雜，在建模時需要對該系統做相應的簡化處理[9]。將輸送帶簡化為具有幾何變形能力的桿；系統的橫向振動影響很小，可忽略；托輥的旋轉部分的等效質量均勻分布于承載區段；系統運行阻力沿輸送帶縱向均勻分布，并且阻力系數與輸送帶速具有線性關系；物料質量均勻分布于輸送帶；所有張緊裝置、驅動裝置和改向滾筒均設為剛性；纏繞在滾筒上的輸送帶質量忽略不計并且設為剛性。

為了對整個出渣系統進行受力分析，需要對整個系統進行單元劃分，輸送帶按照50 m長度進行單元劃分，承載部分有131個輸送帶單元、3個改向滾筒單元、4個驅動單元、1個張緊滾筒平動單元和1個張緊滾筒轉動單元，再加上回程的131個輸送帶單元，總計271個單元。劃分單元后建立的Kelvin動力學模型如圖2所示。

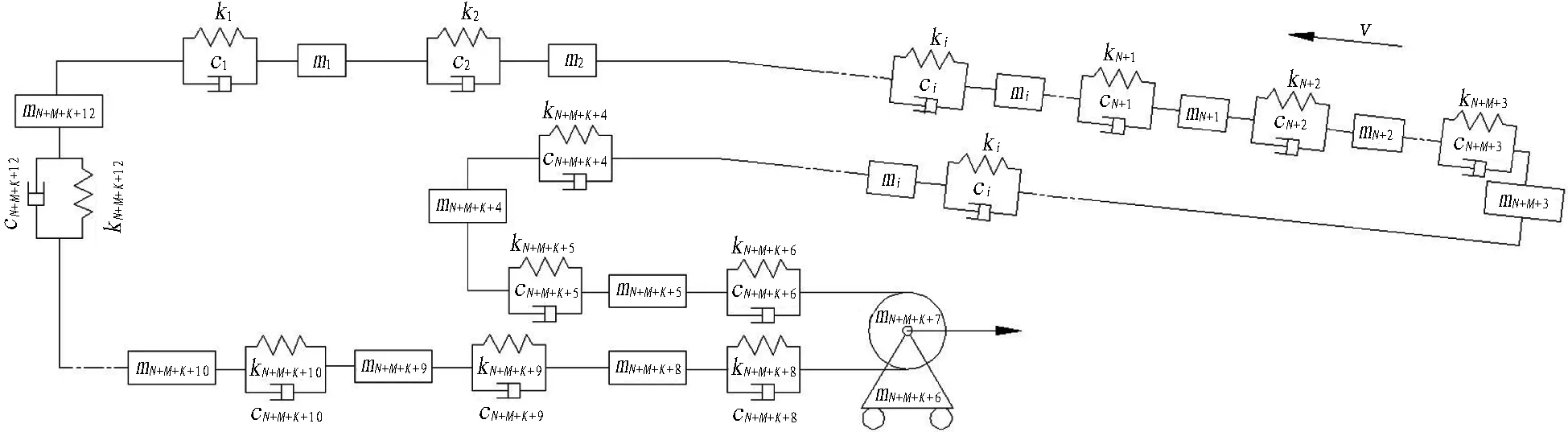
圖2 連續帶式出渣機Kelvin動力學模型

1.3 系統動力學方程

通過連續帶式出渣機的動力學模型分別對各單元進行受力分析，結合各單元動力學方程，整理得到整個出渣機系統的動力學方程：

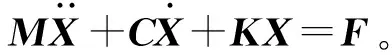
(1)

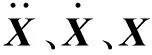
2 起動仿真

2.1 仿真算法

該連續帶式出渣機采用CST系統軟起動[10]。在控制器中設置特定的加速度曲線，控制出渣機系統起動加速度的變化，就能使系統按照一定的速度進行起動，從而減少沖擊保護設備。

在速度曲線確定的情況下，未知量是系統驅動力，可以通過系統動力學方程求解。運用基于功率跟蹤控制[11]的Wilson-θ算法[12]來求解多驅動連續帶式出渣機系統的動力學方程，用Matlab編寫算法程序，并在特定的加速度曲線軟起動條件下進行動態仿真，可得到各單元的速度、加速度、位移和張力等值的變化情況。

仿真時長350 s，頭部第1驅動滾筒第1時間按照輸入的加速度曲線起動，整個加速階段持續200 s，且設置頭部第2驅動滾筒在第8 s開始起動，中間第1驅動滾筒在第50 s開始起動，中間第2驅動滾筒在第58 s開始起動，仿真時間步長設置為0.2 s，Wilson-θ算法中θ值取1.4[13]。將表1中傳統設計主要參數帶入計算程序，即可得到仿真結果。

2.2 起動曲線

2.2.1 常用起動曲線

為探索該連續帶式出渣機的最優起動方式，此次仿真用到的常用起動曲線有Harrison正弦、拋物線、Nordell三角形和梯形4種加速度起動曲線[14]。

這4種常用起動曲線均為連續加速且沒有突變，滿足軟起動的基本要求。它們的起動特性對比見表2。由表可知，當加速時間T夠大時，4種加速度曲線的沖擊度都很小，從理論上講可以作為連續帶式出渣機的起動曲線。

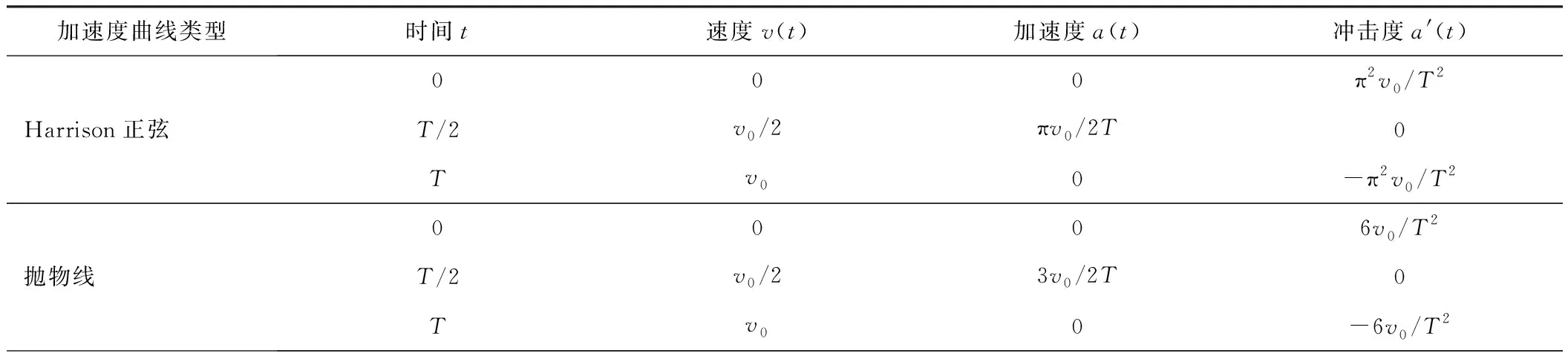
表2 4種常用起動曲線特性分析

表2(續)

注：T為仿真時間；v0為額定運行速度；N為梯形加速度曲線中控制加速度的常數，其值為大于3的整數，本文取100。

2.2.2 正弦組合曲線

考慮到4種常用加速度曲線都有一定的峰值，峰值過大對系統起動有不利影響，因此為了得到峰值較小的加速度曲線，提出一種正弦組合起動加速度曲線。該組合曲線的速度v(t)曲線公式、加速度a(t)曲線公式分別如式(2)和式(3)所示，其中k為待定系數。當額定運行速度v0=3.15 m/s，仿真時間T=200 s，k=16時，加速度a(t)極值最小。

靜止狀態下，輸送帶因為受到重力的作用，會發生

下垂現象，可在起動仿真中設置低速爬行段，從而保證能夠張緊處于自然松弛狀態下的輸送帶，一般設計目標帶速的5%～10%作為低速爬行速度[11]。因此，在式(2)和式(3)中引入爬行段，得到速度v(t)曲線公式(4)和加速度a(t)曲線公式(5)。

(2)

(3)

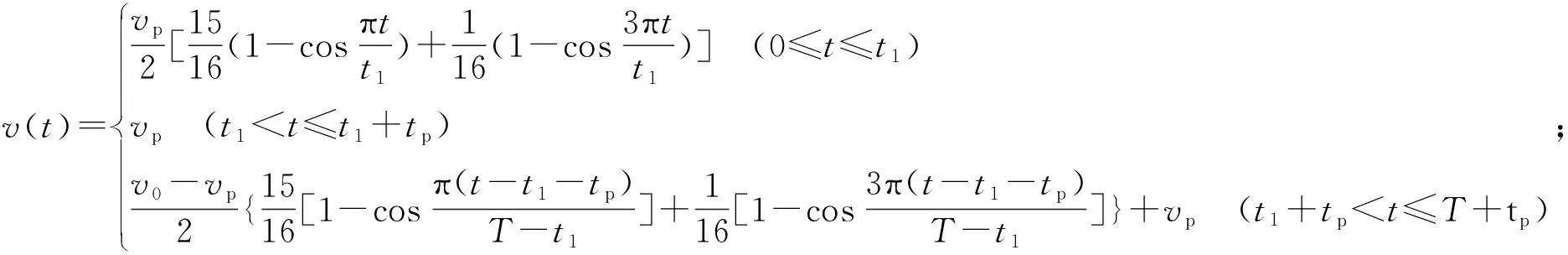
(4)

(5)

式(4)—(5)中：vp為爬行段爬行速度；t1為達到爬行速度所需時間；tp為爬行段時間形變。

3 仿真結果及分析

3.1 4種常用起動曲線仿真結果

把4種常用起動曲線分別輸入程序，進行仿真，經過分析整理得到在不同起動曲線下，連續帶式出渣機系統單元的速度、加速度、驅動力、驅動功率、張力及張緊裝置位移的變化情況，見表3。其中，張緊裝置的位移反映了輸送帶的形變。

由表3可以看出： 1)采用三角形加速度曲線起動方式時，系統驅動力最終呈周期性波動變化，會對出渣機系統造成較大沖擊；采用梯形加速度曲線起動方式時，起動速度不穩定且有突變，驅動力波動變化幅度較大；因此，三角形加速度曲線和梯形加速度曲線都不適合作為帶式出渣機的起動曲線。2)采用正弦加速度曲線和拋物線加速度曲線起動方式時，系統各參數都符合要求，起動沒有突變，驅動力也趨于穩定且低于傳統設計值。

表3 4種常用加速度曲線仿真結果

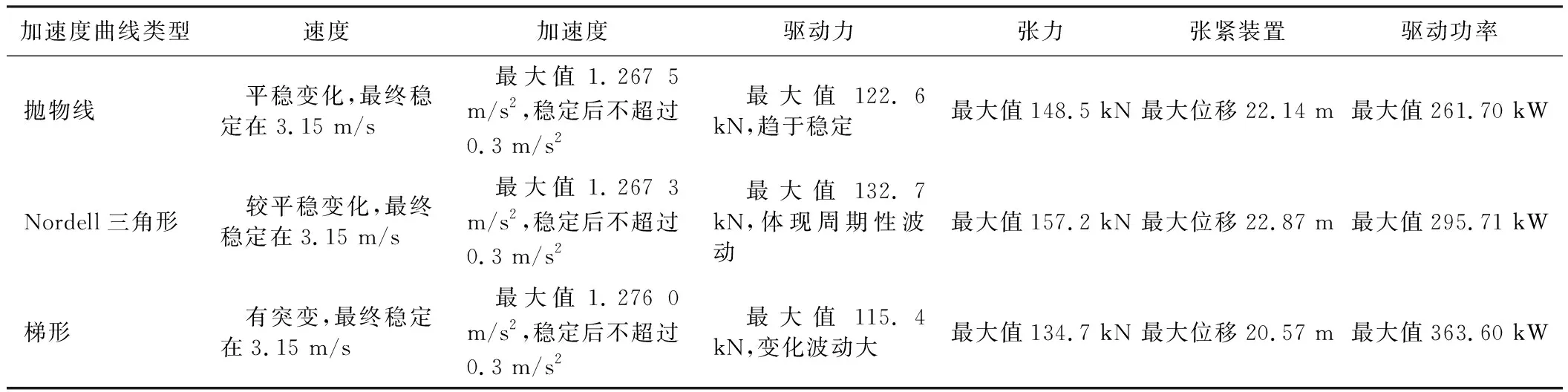
表3(續)

3.2 正弦組合曲線仿真結果

在正弦組合曲線起動仿真中，設定vp=0.315 m/s，t1=35 s，tp=35 s，仿真結果如圖3—8所示。

圖3為輸送帶單元速度變化曲線圖。在剛開始起動0～10 s內某些單元的速度為負值，這是由于輸送帶與水平呈6°傾角，在重力的作用下會出現輸送帶打滑現象，因而可能產生一定的負速度。這一現象可以通過增加張緊裝置、提供預緊力得到解決。

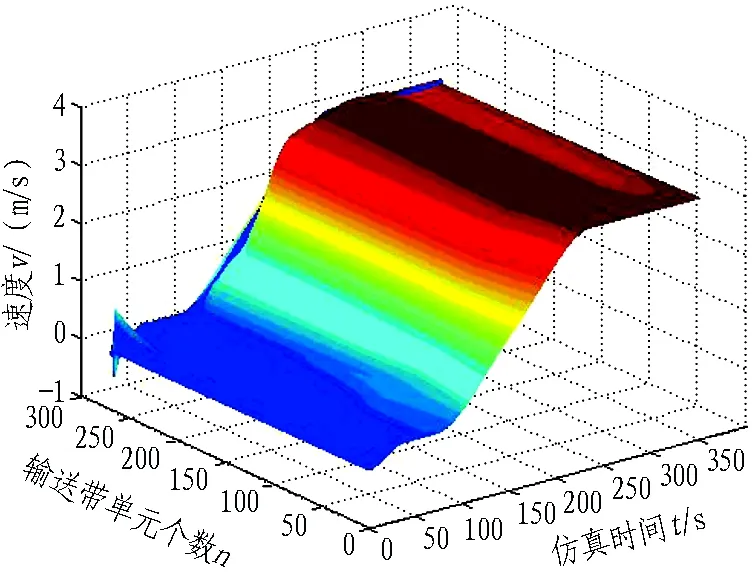
圖3 組合正弦曲線仿真速度變化曲線

圖4為帶式出渣機頭部、中部及尾部的速度變化曲線圖。從圖中可以看出，帶式出渣機頭部單元最先起動，40 s后中間驅動單元開始起動，在第70 s時尾部單元起動。

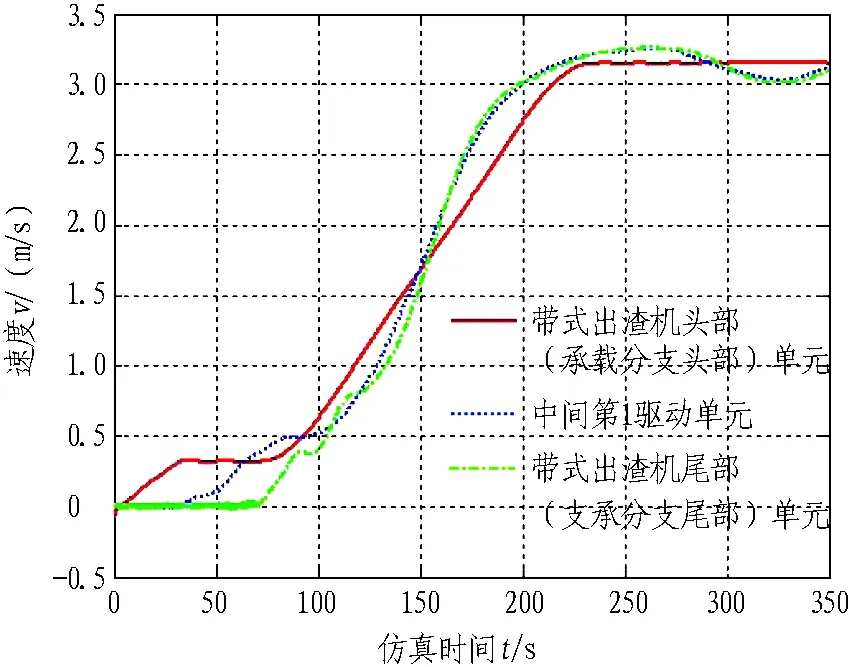
圖4 帶式出渣機頭部、中部、尾部速度變化曲線

Fig. 4 Velocity variation curves of head, center and tail of belt conveyor

結合圖3和圖4可以看出，在起動200 s后帶式出渣機各單元速度均穩定在3.15 m/s附近。起動穩定、連續，滿足設計要求。

圖5為輸送帶各單元的加速度變化曲線圖。由圖可知，在40 s左右張緊裝置附近的輸送帶單元有較大的加速度突變，最大值為1.269 m/s2；除此之外，整個起動過程中系統的加速度均不超過0.3 m/s2，沒有突變。

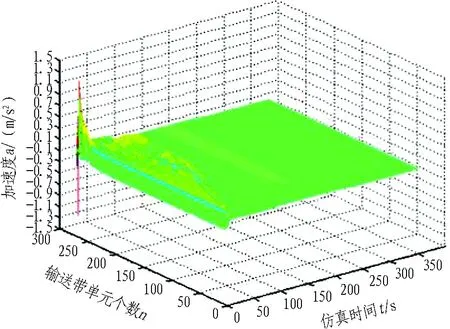
(a) 三維圖

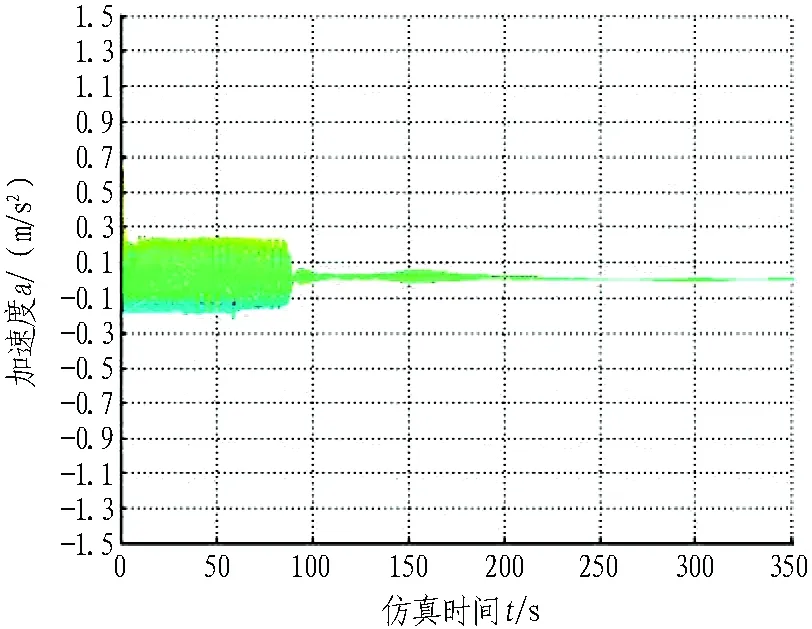
(b) 平面圖

圖6為系統驅動力變化曲線圖。頭部第1驅動、頭部第2驅動、中間第1驅動、中間第2驅動滾筒單元的驅動力最大值分別為110.37、100.93、78.35、79.26 kN，且最終穩定在75 kN左右。其最大驅動力為110.37 kN，相比于正弦加速度曲線的124.96 kN減少了11.68%。

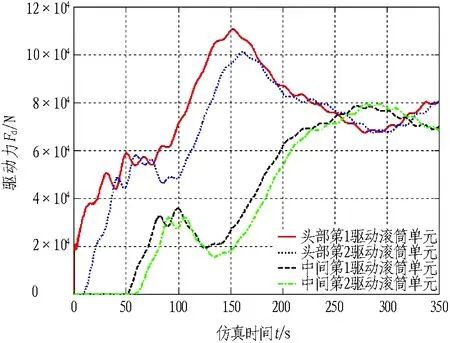
圖6 組合正弦曲線仿真驅動力變化曲線

Fig. 6 Driving force curves of simulation by combined sine curve

圖7為系統驅動功率變化曲線圖。4個驅動功率有著相同的變化規律，其最大值均為253.12 kW，最小值為212.06 kW，且最終都穩定在235 kW左右。可見其滿足機頭雙驅+中間雙驅1∶1的功率配比要求。

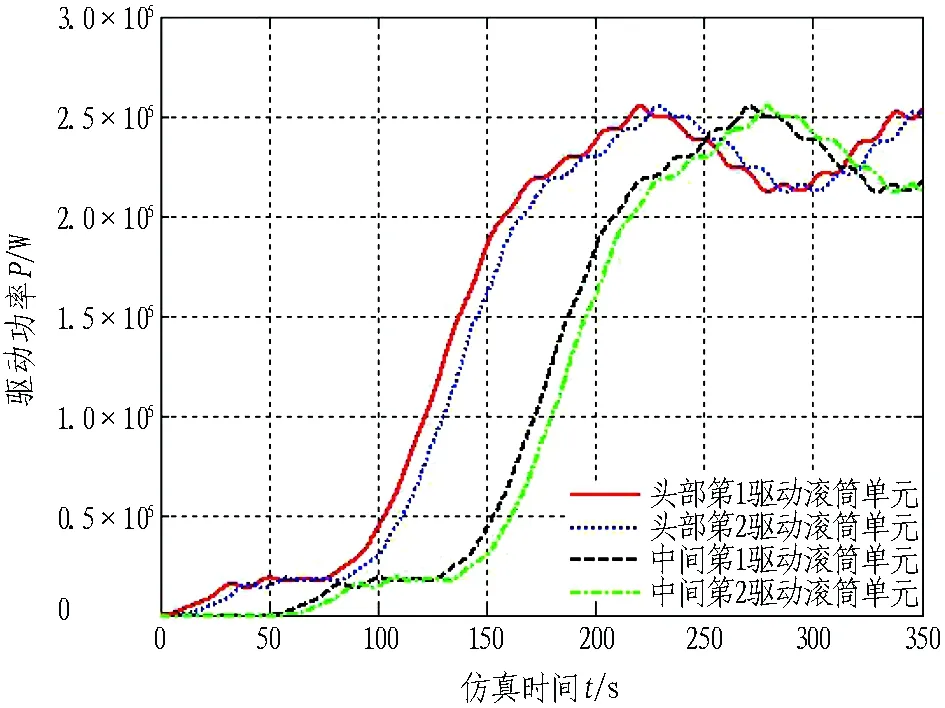
圖7 組合正弦曲線仿真驅動功率變化曲線

Fig. 7 Driving power curves of simulation by combined sine curve

圖8為輸送帶單元的張力變化曲線圖，其中靠近頭部驅動裝置的輸送帶單元的張力值最大，該單元在105.20 s時達到最大張力值124.62 kN，這比采用4種常用起動曲線起動時的最大張力都要小。此時，如果選取輸送帶型號為PVG1250S[15]，可通過式(6)求得其安全系數值為8.02>7，依舊滿足強度要求，而相比采用PVG2500S，其輸送帶強度可降低6個級別。

(6)

式中：m為輸送帶安全系數； [m]為輸送帶許用安全系數，取7；σd為輸送帶強度，N/mm；Smax為輸送帶最大張力，kN。

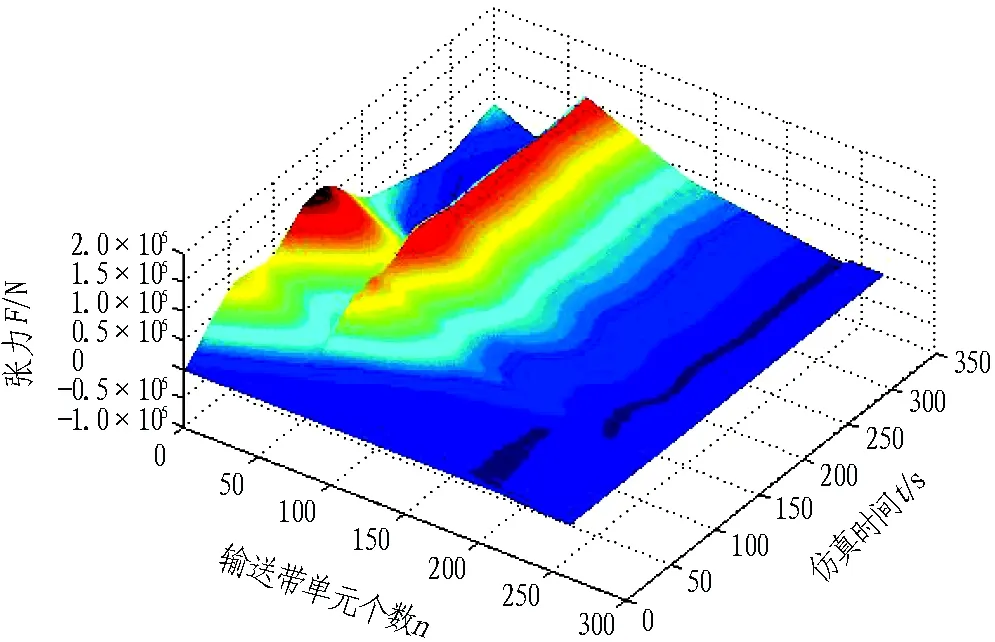
圖8 組合正弦曲線仿真張力變化曲線

圖9為張緊小車的位移變化曲線圖，它反映了輸送帶的變形量。由于輸送帶材料本身的松弛特性，受到驅動力的作用會有一定的變形量，此時張緊小車便會通過自身的移動來補償輸送帶的變形量。張緊小車在155.80 s時位移達到最大值18.10 m，200 s后位移穩定在7 m左右。

Fig. 9 Displacement curves of tensioning device of simulation by combined sine curve

3.3 仿真結果分析

采用CST軟起動系統時，三角形和梯形2種加速度起動曲線不適合作為該帶式出渣機的起動曲線。正弦、拋物線及正弦組合加速度起動曲線可作為其起動曲線，且此時得到的輸送帶最大張力、單驅動功率等關鍵設計參數均大幅低于傳統設計值，表明原本的設計參數獲得了優化。

采用正弦組合曲線起動時，系統最大驅動力取得最小值為110.37 kN；皮帶最大張力取得最小值為124.62 kN，比傳統設計值268.77 kN減小了53.63%；系統張緊裝置最大位移也取得最小值為18.10 m；同時，系統最大單驅動功率也取得最小值為253.12 kW，比傳統設計值400 kW降低了36.72%。

可見，在這5種起動曲線中，正弦組合曲線為該系統的最優起動曲線。

4 結論與討論

通過對連續帶式出渣機建立離散動力學模型及仿真模型，探究其最佳起動方式，取得了不同起動曲線下的仿真結果。研究結果表明：

1)采用適當的起動曲線，經計算機動態仿真得到的參數設計值要比傳統設計值更優，此設計方法優于常規設計。

2)正弦加速度曲線、拋物線加速度曲線及正弦組合曲線都可以作為連續帶式出渣機的起動曲線。

3)采用正弦組合曲線起動效果最好，各項參數值最優。此情況下驅動設備及輸送帶均可降低指標，輸送帶強度最多能降低6個等級，可減少投資成本。

4)在一定的運行速度下，各驅動的起動時間與整個系統加速時間有關。為保證效率和起動要求，最終確定加速時長200 s，其間頭部第2驅動滾筒起動時間為第8 s，中間第1驅動滾筒起動時間為第50 s，中間第2驅動滾筒起動時間為第58 s，從而使得該連續帶式出渣機平穩起動。

5)在仿真過程中，帶式出渣機起動平穩，并且是一個逐級起動的過程，速度最終穩定在3.15 m/s，證明了離散動力學模型的正確性。

通過動態仿真設計得到了優于常規設計方法的參數值，且這些參數具有一定的參考意義，但是建立的動態模型相對于實際情況有所簡化，并不能完全地模擬實際工況。如果將該方法用于實際生產設計，還需要用實體進行進一步試驗。