過渡金屬硫族化合物柔性基底體系的模型與應用?

周愈之1)2)3)

1)(北京應用物理與計算數學研究所,北京 100094)2)(北京應用物理與計算數學研究所鄧稼先創新研究中心,北京 100088)3)(中物院高性能數值模擬軟件中心,北京 100088)(2018年8月22日收到;2018年9月25日收到修改稿)

柔性基底體系是晶體外延生長領域于20世紀90年代提出的概念.其核心思想是利用超薄的基底,使其在外延生長時能同時與外延晶膜發生應變,以抵消二者之間的晶格失配,從而減少外延晶膜中的位錯,提高晶膜的質量.但是人工制備性能優良的超薄基底往往需要較為復雜的工藝.另一方面,過渡金屬硫族化合物由于其層狀結構特性和層間較弱的范德瓦耳斯相互作用,是天然的柔性基底.本文介紹近幾年來新發展的過渡金屬硫族化合物柔性基底體系的模型及應用.以Au-MoS2作為柔性基底外延生長的原型,結合密度泛函理論、線性彈性理論以及位錯理論構建模型,并根據計算結果解釋了早先利用透射電子顯微鏡觀測到的Au薄膜在MoS2上外延生長的相關實驗現象.此外,本文還介紹了受到該理論模型啟發的相關實驗工作,特別是利用Au薄膜分離大面積、單層、高質量MoS2的技術.最后,討論了在該領域內值得關注和進一步探索的理論問題.

1 引 言

過渡金屬硫族化合物(transition metal dichalcogenides,TMDCs),特別是二硫化鉬(MoS2),由于其類似石墨烯的層狀結構、優良的半導體電學性質以及在光電子器件和二維功能材料中巨大的應用潛力,近年來引起了相關領域極大的研究興趣[1?6].在制備相關器件時,需要將其他材料在TMDCs上生長,或者將TMDCs生長在其他材料之上.因此,Au薄膜在MoS2上的生長值得作為典型體系進行深入研究.事實上,晶體生長領域的學者們早在二十世紀六七十年代就通過幾乎是最早的原位與非原位透射電子顯微鏡(in situ&ex situTEM)對Au在MoS2上的生長進行了詳細的研究[7?11].實驗上觀察到的一個顯著現象是在MoS2基底上的島狀Au薄膜幾乎完全是{111}朝向生長,并且晶膜的?110?方向幾乎平行于基底的?11ˉ20?方向(雖然有約±0.25?的微小偏離).MoS2基底上的Ag薄膜也有類似的現象.另外,還通過TEM證實了Au薄膜中失配位錯的存在[11].

雖然Jesser和Kuhlmann-Wilsdorf[8,12]利用當時已有的理論手段模擬了Au薄膜的生長和演化,但其根本是基于對界面性質的唯象認識.同時,MoS2被認為是塊體基底,沒有考慮層間的范德瓦耳斯(van der Waals,vdW)相互作用.在傳統外延生長模型下考察該體系時,認為基底無窮厚不會產生形變,只有薄膜產生形變.此時考慮體系總的彈性能,會發現Au的{111}朝向并不是能量最低的構型.{001}朝向與旋轉的{111}朝向(rotated{111},簡記為R{111})的能量都較{111}朝向更低.這三種朝向的構型以及它們彈性能隨著薄膜厚度的變化如圖1所示.最近,根據MoS2的vdW材料層狀結構特性,我們提出了TMDCs柔性基底外延生長體系的理論模型[13].以Au-MoS2為原型,結合密度泛函理論(density functional theory,DFT)計算、線性彈性理論和位錯理論,并加入表面、界面能的影響,我們證明了在柔性基底的模型下,Au薄膜的{111}朝向為能量最低的構型,如圖1(e)所示.另外,我們還根據模型給出的位錯密度估算了Au薄膜的晶向與MoS2相應晶向的偏離值,這一數值與實驗上的觀測值符合得很好[7].

該理論模型的提出馬上引起了多位實驗學家的關注與興趣.加州伯克利大學Javey團隊的Kiriya等[14],華東師范大學的白偉、唐曉東團隊[15],烏克蘭國家科學院的Borodinova等[16]都利用該模型解釋了他們各自在MoS2基底或其他類似基底上外延生長時所觀察到的晶向關系、薄膜形貌、生長機理等.此外,鑒于計算結果顯示Au與MoS2界面處Au—S鍵強度較高,可以利用外延Au薄膜來操控、分離單層MoS2.受該思想的啟發,我們與加州伯克利大學Javey團隊的Desai等合作,利用Au膜成功分離了大面積同時具有幾乎完美光電學性質(optoelectronically-perfect)的單層MoS2[17].這項成果可以為發展大規模基于TMDCs的光電學器件提供重要的技術基礎.

本文第2節介紹早期的柔性基底外延生長;第3節以Au-MoS2為原型體系,重點介紹基于TMDCs柔性基底的理論模型;第4節介紹與該理論相關的一些實驗工作,特別是利用外延生長的Au薄膜分離大面積、高質量的單層MoS2的技術手段;第5節討論未來值得關注和進一步探索的理論問題.

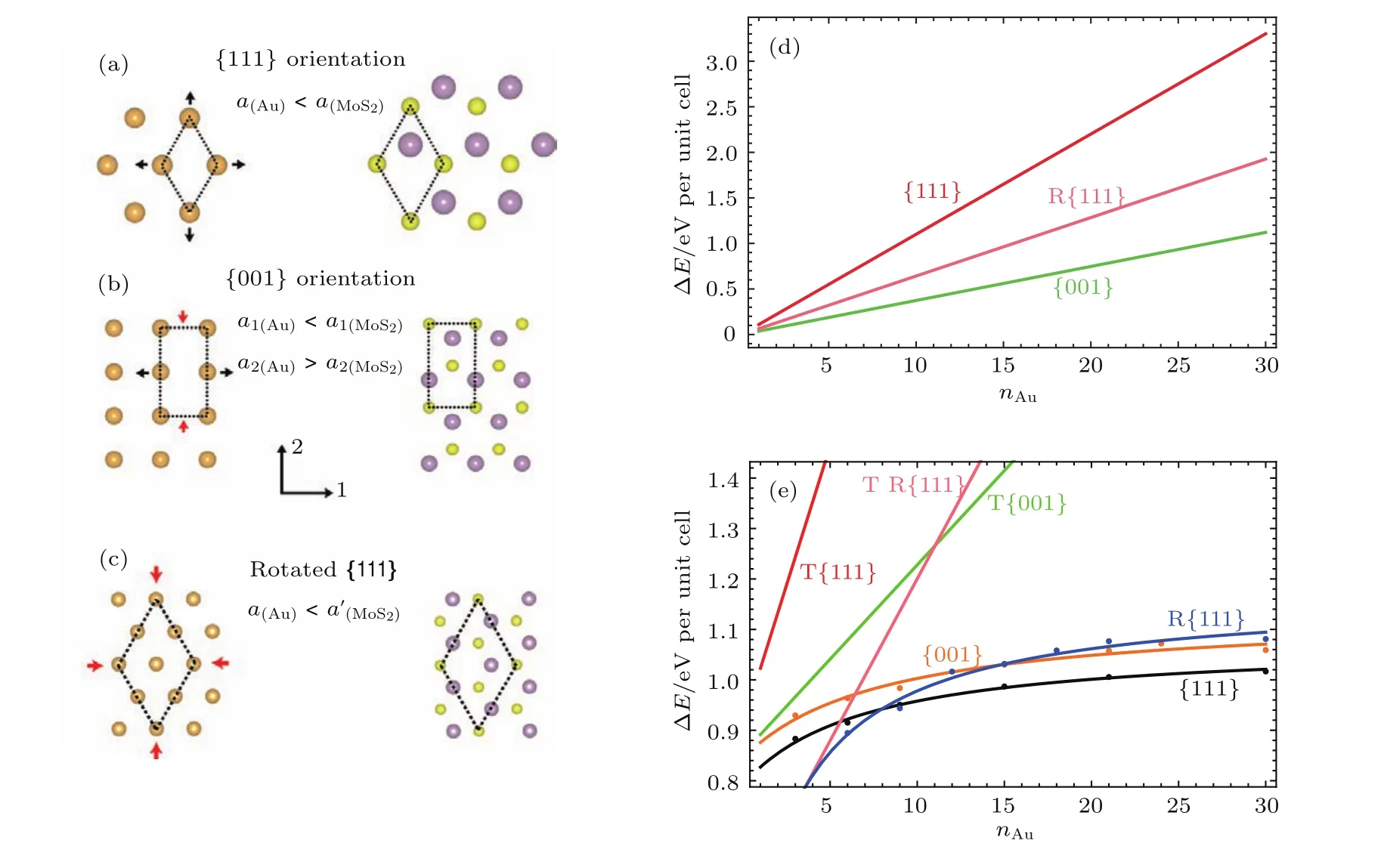
圖1 (a){111}朝向、(b){001}朝向以及(c)旋轉的{111}朝向(R{111})的界面構型示意圖;(d)在傳統外延生長模型下,三種構型的彈性能隨著厚度的變化;(e)在考慮了表面能與界面能的貢獻后,傳統外延生長模型(有T前綴)依然預測{001}為能量最低的構型;而在柔性基底外延生長模型下(無T前綴),{111}朝向的能量是最低的[13]Fig.1.Atomic configuration of(a){111}orientation,(b){001}orientation and(c)rotated{111}orientation interfaces;(d)under the traditional epitaxy model,the elastic energy in three orientations,assuming a rigid MoS2 substrate;(e)with the account for the surface and interface energies,traditional epitaxy still predicts the{001}orientation to be the lowest energy configuration(for the most range of thickness);while in the compliant substrate epitaxy(curves without“T”prefix),{111}orientation has the lowest energy[13].

2 早期的柔性基底外延生長

柔性基底外延生長的模型最早于20世紀90年代由Lo提出[18],但最原始的思想,模型計算和實驗展示可以追溯到20世紀80年代Woltersdorf和Pippel[19,20]關于金屬生長的工作.早期的柔性基底模型與本文介紹的基于TMDCs柔性基底模型的核心特性大體相同,即超薄的基底在外延生長時能同時與外延晶體發生應變以抵消晶格失配.但早期的柔性基底都依賴于人工手段的制備,而復雜的工藝限制了這些模型的大規模推廣和應用.本節對早期典型的柔性基底外延生長的模型做簡要介紹.

1)懸空柔性基底(freestanding compliant substrate).其基本思想是利用刻蝕的手段制備薄膜式的懸空柔性基底.這方面最早的研究是Chua等[21]利用支點上的GaAs懸空薄膜生長高質量的In0.14Ga0.86As膜,如圖2(a)所示.但這項技術的缺點在于柔性基底會由于外延薄膜中的應力而產生彎曲和破裂.另一種懸空柔性基底是通過圓平臺基座所實現.Jones等[22]利用光刻蝕技術制備了In0.05Ga0.95As的基座式懸空柔性基底,并在其上生長了In0.15Ga0.85As的外延薄膜以及In0.4Ga0.6As的量子阱,其結構示意圖如圖2(b)所示.但基座式的柔性基底結構非常脆弱,同時基座表面也很難保持水平[23].

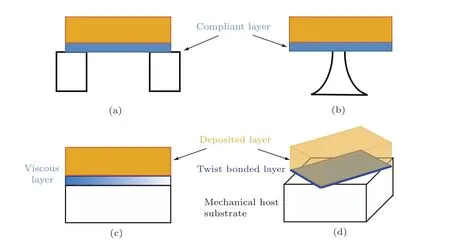
圖2 早期柔性基底外延生長的幾種典型模式 (a)空洞式懸空柔性基底;(b)基座式懸空柔性基底;(c)黏性層柔性基底;(d)扭曲層柔性基底Fig.2.Models of early compliant substrate epitaxy:(a)Hole-freestanding compliant substrate;(b)pedestal-freestanding compliant substrate;(c)viscous layer compliant substrate;(d)twist-bonded layer compliant substrate.

2)黏性層柔性基底(viscous layer compliant substrate).其基本思想是利用非晶態的SiO2、玻璃(含30%—50%B2O3)或者在生長溫度下呈液體的金屬In,形成具有黏性特性,幾乎無摩擦的柔性基底,如圖2(c)所示.典型性的工作可參考Powell等[24]、Hansen等[25],以及Carter-Coman 等[26]的文章.這類方法的困難在于制備足夠薄的黏性層膜,其效率也較下面介紹的扭曲層柔性基底偏低.

3)扭曲層柔性基底(twist-bonded layer compliant substrate)最早由Ejeckam等[27]提出,其基本思想是利用與固定基底(mechanical host substrate)相同的材料作為柔性基底,但該柔性基底層與固有基底間存在較大的扭曲角度(large twist angle),如圖2(d)所示.Ejeckam等[27]進而實現了3 nm厚的、具有不同扭曲角度的GaAs柔性基底.許多研究表明,當扭曲的角度大于15?—20?時才能形成有效的柔性基底.該類柔性基底具體的制備工藝在Bourret[23]和Ayers[28]的綜述中都有較詳細的介紹.原則上,該類柔性基底技術的適用性較前兩種更廣.

綜上可見,早期柔性基底外延生長模型依賴于人工手段(腐蝕、光刻等)制備出柔性基底.制備性能優良的柔性基底往往對工藝的精度有非常高的要求,同時制備過程也較為繁瑣,從而限制了這些模型進一步發展和應用.下面所要重點介紹的基于TMDCs的柔性基底體系,利用vdW材料天然的層狀特性實現柔性基底,從而巧妙地回避了傳統柔性基底在制備工藝上的種種問題.

3 Au-MoS2的柔性基底外延生長體系

我們在仔細考察了Au在MoS2上的生長后發現[13],MoS2等TMDCs由于其層狀的結構,以及層間較弱的vdW相互作用,當外延晶膜與基底能形成較強的化學鍵時,最頂層的基底天然成為柔性基底.而MoS2的柔性基底特性在解釋Au在MoS2上外延生長的相關實驗現象時非常關鍵.

3.1 理論模型

該柔性基底模型[13]的基礎是通過線性彈性理論和位錯理論描述體系的能量變化,并借助DFT計算給出關鍵的材料參數,如彈性常數、表面和界面能等.Au-MoS2柔性基底外延生長體系的示意圖如圖3所示.相對于材料各自的塊體狀態而言,體系的能量變化可以表示為

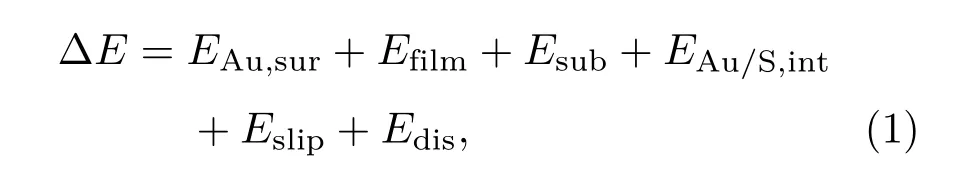
其中EAu,sur是Au膜表面的應變彈性能,Efilm是Au膜塊體部分的彈性能,Esub是基底的彈性能,EAu/S,int是Au-MoS2界面的應變彈性能,Eslip是最頂層MoS2與其余MoS2基底間的滑移能,Edis是晶膜中產生位錯的彈性能.下面對各部分能量進行介紹.

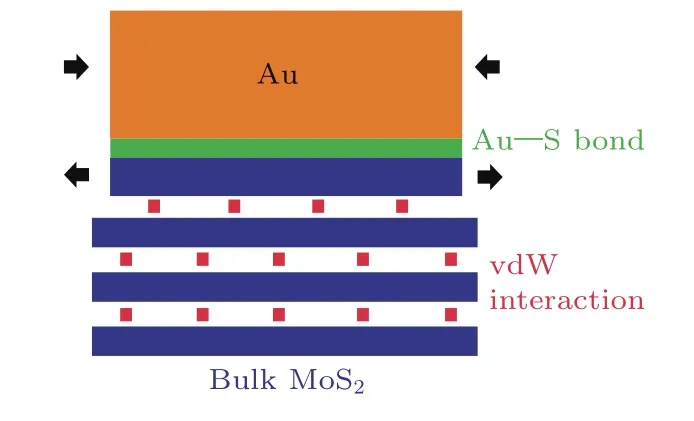
圖3 Au-MoS2柔性基底外延生長體系示意圖Fig.3.Illustration of the compliant substrate epitaxy system of Au-MoS2.

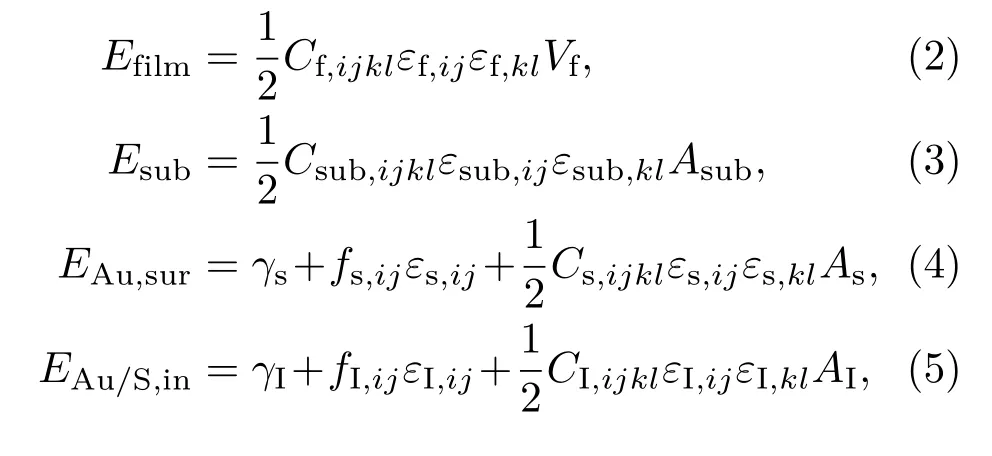
1)彈性能項.在(1)式中,右邊前四項的表達式可以根據線性彈性理論給出:其中Cf,ijkl,Csub,ijkl為晶膜和最頂層基底的彈性常數(應變張量以同樣的方式定義);γs和γI分別為表面能與界面能;由于表面與界面都依賴于塊體晶格而存在,故沒有穩定性的限制,從而其彈性能表達式含有一階項fij;Vf為晶膜在塊體材料中的平衡體積;Asub,As和AI分別為基底、表面和界面的平衡體積,特別地,表面與界面的平衡面積As和AI取為Au晶膜的相應平衡面積Af,而Asub為單層MoS2單胞的平衡面積.

在上述參數中,除了表面彈性能與界面彈性能的零階項(γs,γI)、一階項(fI,ij,fs,ij)與二階項(Cs,ijkl,CI,ijkl),其他參數都由DFT計算直接獲得.而上述未知的表面與界面參數則是根據上面獲得的表達式,擬合DFT計算所得的不同層數Au膜加單層MoS2體系的能量得到.具體的計算和擬合細節請參考關于Au-MoS2柔性基底理論模型的文章[13].

2)基底間的滑移能.對于最頂層MoS2與其余MoS2基底間的滑移能,通過考察雙層MoS2體系的層間相互作用進行估算.Au-MoS2體系中,頂層MoS2的平均應變約在?5%.因此,取第一個雙層MoS2體系為無應變體系作為基準.每層MoS2含20×20個原胞,兩層MoS2的堆疊方式與塊體中的一致.第二個雙層體系中,其中一層MoS2被施加了?5%的雙軸應變,而另一層保持不變.兩個體系的層間相互作用能量差為柔性基底體系滑移能的估計值.層間的相互作用由Grimme[29]所提出的含vdW修正的DFT D2表達式計算得到:

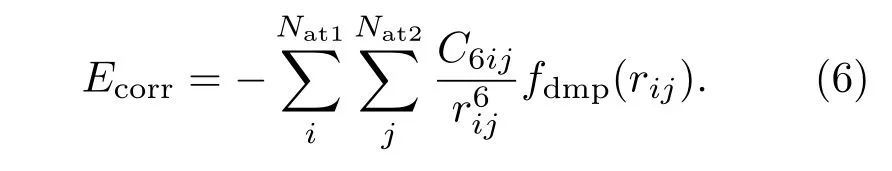
這里,角標i,j分別遍歷第一層與第二層中的所有原子;rij為兩原子間的距離.C6ij是描述兩原子間的vdW相互作用強度的參數,與兩個原子的原子種類有關,

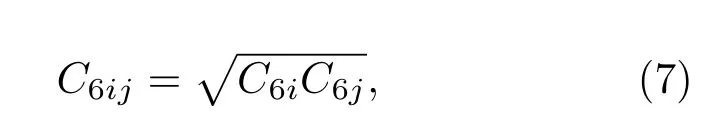
其中C6i和C6j僅與元素種類有關,與其所在的化學環境幾乎無關;fdmp(rij)為阻尼函數,作用是減少奇異性以幫助求和的收斂.此外,Grimme還在文獻[29]中提供了元素周期表中前五行元素的C6i數值.

根據我們的計算,?5%應變所產生的滑移能為每單胞5 meV,故這里考慮的所有Au-MoS2體系中的滑移能的量級都應在1 meV.相較于彈性能和位錯能的貢獻,在目前的模型中該部分的能量貢獻可以暫時忽略.

3)失配位錯能.當失配位錯出現時,晶格常數不同所導致的應變可以得到部分抵消,但代價是產生了位錯的形成能.我們在討論Au-MoS2體系中Au膜的位錯時做了這些假設[13]:①位錯為全位錯(pure dislocation);②一組相同的位錯平行排列,并具有統一的間距.根據位錯理論,一組間距為p的位錯的形成能為

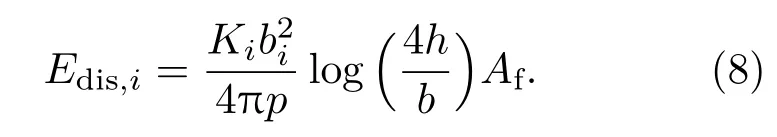
(8)式中,h為膜的厚度,Af為膜的面積,b為伯格斯矢量(Burgers vector),Ki是晶格各向異性能的參量,而bi為b在相應方向上的投影組分(各向異性能的定義和計算請參考Hirth等[30]的著作).關于Au晶膜{111},R{111}和{001}朝向中的位錯構型如圖4所示.構型和應變的相互關系的具體分析請參考我們Au-MoS2柔性基底的文章[13].

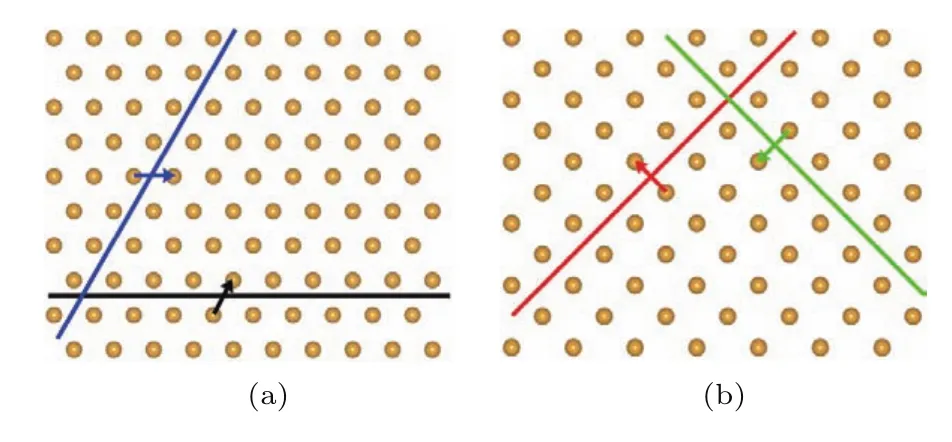
圖4 (a)Au晶膜{111}朝向和R{111}朝向中的位錯構型(俯視圖),其中實線代表位錯的線方向,箭頭代表{111}朝向中的伯格斯矢量,R{111}中的伯格斯矢量大小相等,方向相反;(b){001}朝向中的位錯構型[13]Fig.4.(a)Dislocation geometry in the{111}and R{111}orientation films;solid lines represent the line direction of the dislocation;arrows indicate the Burgers vectors;(b)dislocation geometry in the{001}orientation film[13].

3.2 數值模擬

Au-MoS2理論模型的計算結果分為兩部分.

1)不含位錯能的參數擬合.首先需要在不含位錯的?E表達式中,通過對DFT計算結果的擬合,給出表面和界面的相關彈性參量.(1)式中,給定Au膜的厚度,平衡狀態時?E的表達式由以應變為變量求極小值得到.在求極小時應注意到在Au與MoS2的界面處對二者的應變有晶格匹配的約束條件.同時,晶格對稱性和界面構型對應變矩陣形式也有簡化.以{111}朝向為例,Au晶膜與MoS2都不含剪切應變.此外,由于晶格對稱性的要求,其正交應變在x,y方向上的分量是相等的(ε11=ε22).因此,界面處晶格匹配的約束條件為

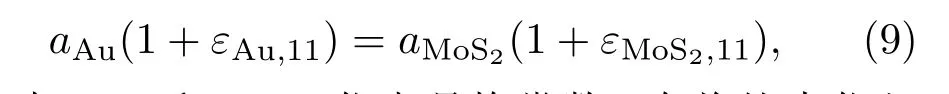
式中,aAu和aMoS2代表晶格常數.在將約束代入?E的表達式之后,將該表達式相對于應變張量中所有的獨立變量求極小.最后再根據極小值的表達式擬合DFT計算所得到的?E以及應變隨厚度所變化的數據.?E擬合結果如圖5中圓點和實線所示.而根據擬合所得到的表面和界面的彈性參數則可應用于后面包含位錯能項的?E的計算.

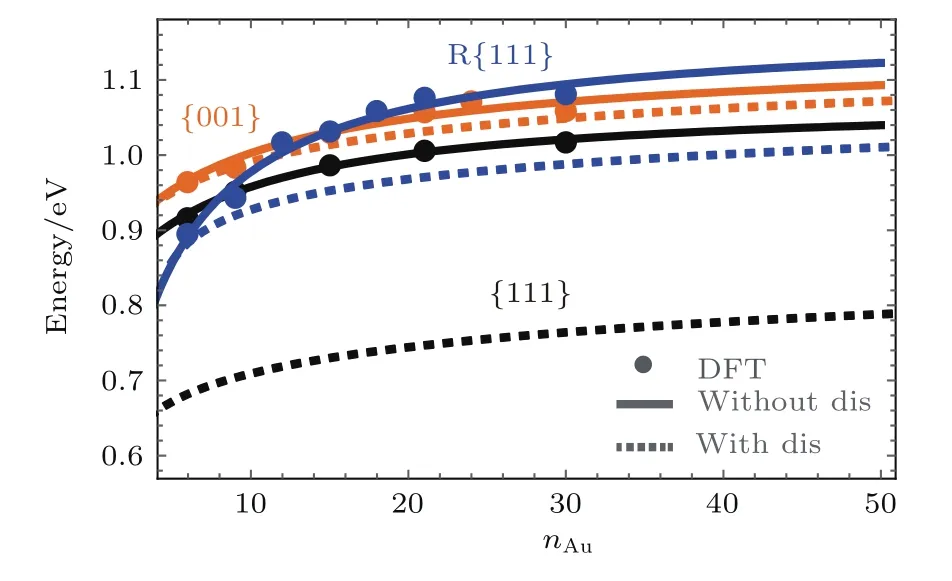
圖5 不同朝向下?E隨Au膜層數變化的曲線,其中實線為不含位錯能項對DFT計算數據(圓點)的擬合結果,虛線為含位錯能項的最終結果[13]Fig.5.?E versus Au thickness for three orientations.Solid lines are the fitting results of?E without the dislocation energy term to the DFT results(circle).Dashed lines are the final results of?E(with the dislocation term)[13].

2)含位錯能的總結果.在獲得表面和界面的彈性參數后,可以將位錯能的貢獻加入?E.此時,由于位錯的出現,界面處的晶格匹配的約束條件多了位錯對應變的釋放.以{111}朝向為例,此時界面處的約束條件為

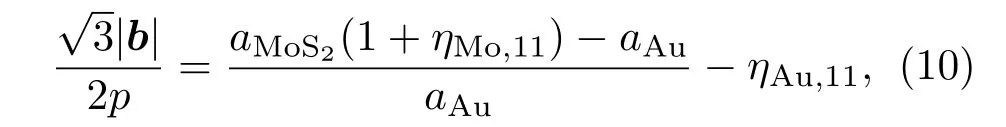
其中等號左邊的部分來自于位錯的貢獻;b和p分別為位錯的伯格斯矢量和間距.同時注意到{111}朝向的對稱性,圖4中的兩組位錯具有相同的間距p.為區別于不含位錯時的約束條件,這里η代表應變.同樣將該約束條件代入含位錯能的?E表達式,再對應變張量的獨立分量和位錯密度1/p求極小值,可以獲得平衡狀態時?E的數值.含位錯能時?E隨厚度的變化如圖5中虛線所示.

3.3 相關討論

與傳統外延生長理論所不同的是,根據Au-MoS2柔性基底的模型,{111}朝向成為了能量最低的外延生長構型,如圖1(e)和圖5所示.這一結果與實驗上觀測到的Au薄膜幾乎都是{111}朝向的現象[7]相符合.除了MoS2柔性基底的特性,還有一個重要因素使得{111}朝向能量更低:即Au-MoS2的界面性質.界面對于穩定性的影響在{111}朝向和R{111}朝向兩種構型的比較中尤為明顯.考慮到這兩種構型唯一的區別就是界面處的結構不同,如圖1所示:在{111}構型中,界面處每一個S原子上方都有一個Au原子,因而Au—S成鍵較強;而在R{111}朝向中,界面處僅有約1/4的Au原子在S原子上方直接成鍵,因而Au—S成鍵較弱.擬合所得的界面能數值同樣體現了這一點:{111}構型的界面能較R{111}的低0.03 eV/?,同時Au—S鍵的強度約為0.3 eV[13].這一認識也與人們早先在硫醇類和二硫化物中發現的Au—S鍵強度相符合[31].因此,Au-MoS2在外延體系中,界面處的Au—S鍵強度也是{111}朝向構型較其他朝向更穩定的重要因素之一.更重要的是,可以通過Au—S鍵操控單層MoS2,因為Au—S的強度要強于層間的vdW相互作用.將在下一節介紹實驗上受到Au-MoS2體系計算結果啟發而實現的大面積單層MoS2的分離[17].

除此之外,該柔性基底模型也可以成功預測實驗上觀測到的Au薄膜與MoS2晶向間的微小偏移(由TEM所得到的Moiré條紋測得)[17].經過仔細分析,我們認為晶向間的微小偏移是由于Au{111}朝向的薄膜中兩組位錯的間距或個數不嚴格一致所導致的[13].理想情況下,圖4(a)中兩組位錯的間距應當嚴格相等.然而,當二者的間距產生微小的偏離?p時,會在畸變張量(distortion tensor)中產生反對稱的旋轉分量,從而導致的旋轉角度為|b|?p/(4p2).根據實驗文獻,TEM照片里的Au膜的大小約為20 nm.同時模型中計算得到的5 nm厚的Au薄膜中位錯的間距約為4 nm.當兩組位錯的個數產生微小的差別(±1)時,可計算得晶膜的旋轉量為±0.26?.這與實驗上觀測到的旋轉量±0.25?符合得非常好[7].

4 Au-MoS2柔性基底的應用:分離大面積單層MoS2

Au-MoS2柔性基底理論模型的提出引起了多位實驗學家的關注與興趣.加州伯克利大學Javey團隊的Kiriya等[14]根據我們的模型[13],推測出當Au納米線在MoS2基底上互成60?生長時,Au與MoS2間的晶向關系很有可能是之前所討論的{111}朝向的構型.華東師范大學的白偉、唐曉東團隊[15]利用柔性基底模型中表面、界面能的概念解釋了SrTiO3基底上MnTe薄膜{111}朝向存在的合理性.烏克蘭國家科學院的Borodinova等[16]認為正是由于柔性基底的特性使得不同Au納米結構能在MoS2基底上生長,并通過實驗展示了在不同生長條件下在MoS2基底上得到的Au納米顆粒、納米線、納米三角形及六邊形薄膜等結構.

目前該模型最重要的應用是分離大面積單層MoS2.如前面所提到的,由于界面處Au—S鍵的強度較高,同時MoS2層間的vdW相互作用較弱,因而可以通過Au—S鍵操控最頂層的MoS2.受這一想法啟發,我們的實驗合作者加州伯克利大學Javey團隊的Desai等[17]通過利用MoS2表面生長的Au膜,成功分離了大面積同時具有幾乎完美光電學性質(optoelectronically-perfect)的單層MoS2[17].

在此,我們對這項技術做簡要介紹:第一步是在塊體MoS2上沉積生長Au薄膜.由于Au—S的成鍵強度要高于MoS2層間的vdW相互作用,同時頂層MoS2中產生的應變減弱了其與下層MoS2的相互作用,因此可以選擇性地剝離最頂層的MoS2.具體分離時使用的是熱剝離膠帶,將最頂層MoS2轉移到目標基底上(Si/SiO2).在轉移之后,再利用化學刻蝕的手段(KI/I2)清除單層MoS2上的Au膜.最后使用丙酮和異丙醇(acetone and isopropyl alcohol)清潔單層MoS2上的殘留物.通過這種方法獲得的單層MoS2,成功率較傳統膠帶分離的方法更高,同時分離出的單層MoS2的面積也至少要高一個量級[17],如圖6(c)所示.進一步的光學和電學的表征實驗證明這種分離方法得到的單層MoS2具有很好的均勻性以及優秀的光電學性質.分離所得的大面積、單層而高質量的MoS2薄膜,為大規模TMDCs器件的發展提供了有力的保證.這項工作引起了該領域科研人員的廣泛關注,并立即為之后的許多綜述所提及[32?34].關于具體分離、表征和測量的實驗細節,感興趣的讀者可以參考文獻[17].

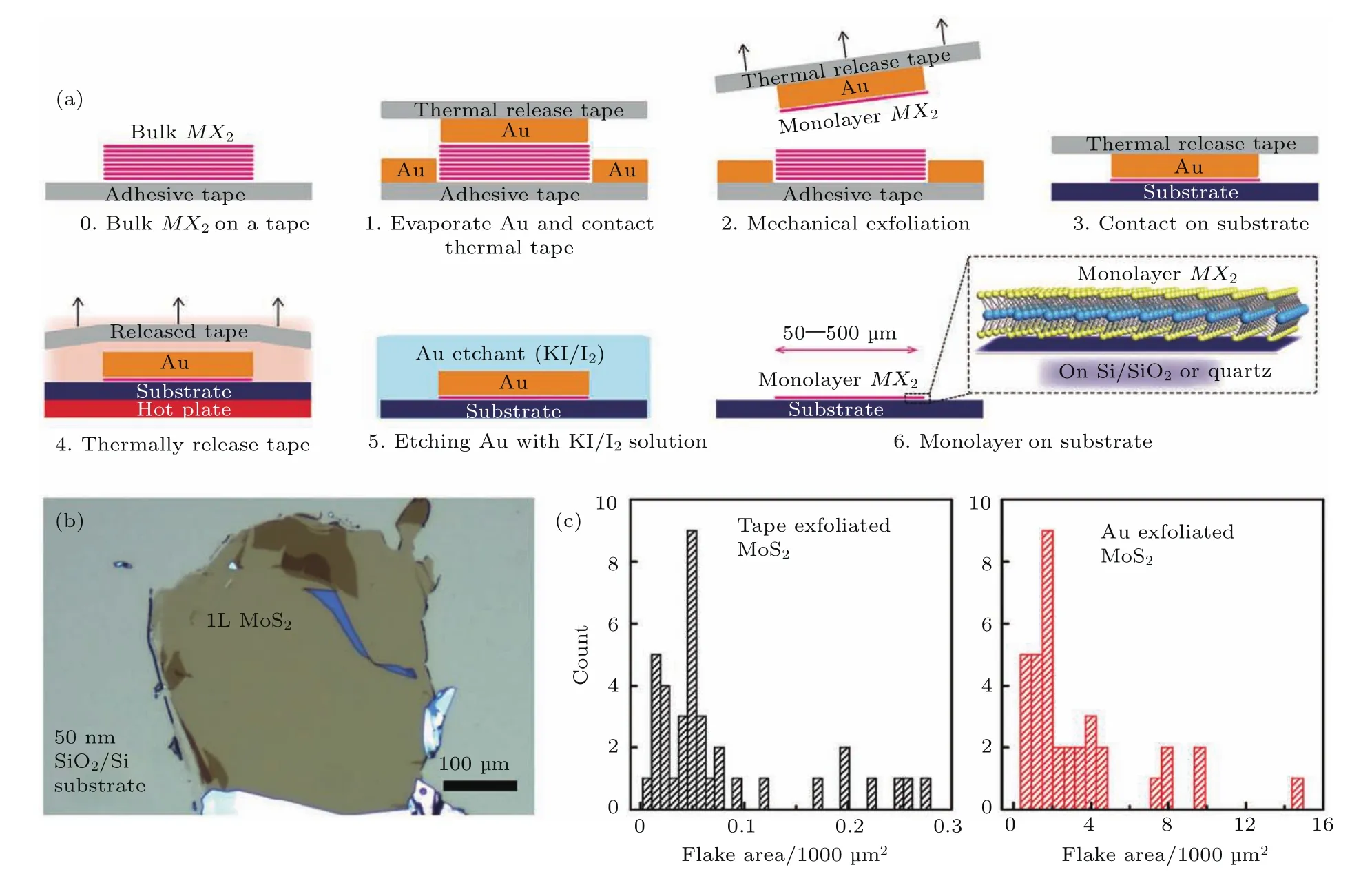
圖6 (a)利用Au晶膜外延生長而實現的分離大面積單層MoS2的實驗步驟示意圖;(b)分離所得的單層MoS2的實際照片;(c)膠帶分離(tape exfoliated)與Au膜分離所得到的MoS2面積的柱狀圖[17]Fig.6.(a)Schematic illustration of the Au exfoliation process;(b)optical microscope image of a large monolayer MoS2 flake;(c)histogram of flake areas for tape-exfoliated versus Au-exfoliated MoS2[17].

5 總結與展望

本文主要討論了基于TMDCs的柔性基底體系的最新理論進展以及應用.我們通過結合DFT、線性彈性理論以及位錯理論,以Au-MoS2作為此類柔性基底外延生長的原型進行了全面介紹.并通過計算結果解釋了早先實驗上觀測到的但傳統外延生長模型無法解釋的實驗現象.著重介紹了受該理論模型啟發,利用MoS2表面生長的Au膜實現分離大面積、高光電學質量的單層MoS2的技術手段.這項技術對于發展大規模TMDCs光電器件有重要的意義.

雖然TMDCs的柔性基底體系在理論和實踐上都取得了許多進展,但仍有不少值得進一步探索的重要問題.

1)其他TMDCs的柔性基底外延生長體系.對Au-MoS2工作一個自然的延伸就是尋找其他類似的TMDCs的柔性基底體系.由于柔性基底外延體系對晶格常數匹配的要求遠低于傳統外延生長(Au與MoS2的晶格失配達到了6%—8%),因而在常見的金屬與TMDCs的組合中,可以找到許多潛在的柔性基底體系.當然,其他二維材料如石墨烯和氮化硼也可以作為柔性基底.這些新的柔性基底體系是否有特殊的性質?是否能將這些特性應用到功能性材料、能源、新型電子器件等領域?這些問題值得進一步探索.同時,根據所需性質設計、尋找柔性基底體系的課題很適合利用高通量計算的手段去研究.

2)分離單層MoS2技術的模擬與優化.優化的核心問題在于尋找最優的Au膜厚度以及膜的形貌圖樣,使得Au膜協助分離單層MoS2時,最頂層MoS2與第二層間的vdW相互作用最弱.DFT計算雖然準確性較高,但構建一層有～5%應變、一層無應變的雙層MoS2體系需要超大超胞(至少千原子量級).同時由于分離過程涉及vdW的相互作用,電子自洽計算以及結構弛豫需要很高的精度.這遠遠超出了現有計算集群的計算能力.折衷的方法或許是使用分子動力學去研究層間vdW相互作用以及層間分離的動力學模式.目前我們認為最合適的分子動力學經驗勢為Liang等[35,36]與Stewart和Spearot[37]發展的,能夠同時描述MoS2層間與層內成鍵的Mo-S經驗勢.最近,伯克利材料系的Chrzan團隊在該方向上已有最新的進展[38].但此經驗勢描述層間分離過程的準確性,以及是否有必要發展新的經驗勢以研究此類問題的必要性,有待進一步的探索和論證.

3)無公度體系的電子結構計算方法.在Au-MoS2柔性基底體系中,頂層MoS2由于其應變數值的任意性,非常可能與第二層MoS2形成無公度體系(incommensurate system),即雖然每層內都具有周期性,但體系整體無周期性.無公度體系也常見于TMDCs的異質結結構.從理論上認識、研究無公度體系對于二維材料的基礎研究和應用有著重要的意義.目前常用的方法是用大超胞的有公度體系去近似無公度體系,進而可以利用傳統的Bloch定理進行電子結構計算[39?41].但是這種近似方法的合理性和準確性仍存在疑問.因此,我們認為很有必要針對無公度體系發展一套高效率與高精度的計算方法.關鍵問題在于利用更嚴格的數學語言和工具去描述無公度體系,并在該框架下發展求解Kohn-Sham方程的系統理論.我們在這方面已有初步的探索.

由衷地感謝中國科學院數學與系統科學研究院劉歆教授以及北京師范大學數學系陳華杰教授的討論.