新型二維壓電聲子晶體板帶隙可調性研究?

廖濤 孫小偉 宋婷 田俊紅 康太鳳 孫偉彬

(蘭州交通大學數理學院,蘭州 730070)(2018年4月5日收到;2018年7月12日收到修改稿)

設計了一種由涂有硬質材料涂層的柱狀壓電散射體周期性連接在四個環氧樹脂薄板上構成的具有大帶寬的新型二維壓電聲子晶體板,并利用有限元方法計算了該聲子晶體板的能帶結構、傳輸損失譜和位移矢量場.研究表明:與二組元材料構成的傳統聲子晶體板相比,新設計的聲子晶體板的第一完全帶隙頻率更低,并且帶寬擴大了5倍;通過在壓電體表面上施加不同的電邊界條件,可以實現多條完全帶隙的主動調控;壓電效應對能帶結構有很大的影響,并且有利于完全帶隙的擴大與形成.基于帶隙的可調諧性,分析了可切換路徑的壓電聲子晶體板波導,結果表明可以通過改變電邊界條件來限制彈性波能量流.

1 引 言

聲子晶體是人造周期性復合結構,它可以有效控制彈性波或超聲波的傳播[1].在這種周期結構中,彈性波在一定頻率范圍內被禁止傳播,這個頻率范圍稱為帶隙.帶隙的存在使得聲子晶體具有廣泛的應用前景,例如用于聲學濾波器、聲波導、噪聲控制、傳感器設計的改進等[2?6].通常,在制造聲學器件時,帶隙的頻率范圍是固定的,表現為被動不可調的帶隙特性.為了實現聲子晶體帶隙的可調諧性,一些功能材料被引入到周期性結構中,如形狀記憶合金、電流變材料、介電彈性體層和磁彈性材料等,通過改變填充物的幾何形狀或通過外部刺激改變構成材料的彈性特性,以調整聲子晶體的能帶結構[7?12].

壓電材料作為一種新型智能材料,因其具有高機電耦合系數和低聲阻抗,尤其是在精確控制位移、快速響應時間和小型器件尺寸方面與其他類型的可調材料如形狀記憶合金、電流變材料等相比更具有優勢,在工業、生物醫學和國防領域具有廣泛的應用[13?16].近幾年,基于壓電材料的聲子晶體引起了廣泛的關注[17?24].Khelif等[20]在壓電聲子晶體板上獲得了完全帶隙;Hsu和Wu[21]在壓電聲子晶體板上獲得了低頻蘭姆波的局域共振帶隙,并得出結論認為:以彎曲為主的板塊模式的共振頻率取決于圓形橡膠填充物的半徑和板坯的厚度;Hsu[22]研究了電邊界條件對壓電聲子晶體板中帶隙的影響,并討論了僅通過改變電邊界條件來控制頻率間隙的可能性;Cro?nne等[23]分別從理論和實驗的角度研究了由壓電復合材料構成的聲子晶體板的帶隙特性,結果表明通過施加周期性電邊界條件可以對布拉格帶隙進行調控;Zou等[24]研究了彈性波在覆蓋有周期性結構涂層的壓電板中的傳播,著重討論了涂層的分布形式和幾何參數對完全帶隙的影響,研究表明具有對稱涂層的聲子晶體板可以產生更寬的完全帶隙,而具有不對稱涂層的聲子晶體板有利于產生多帶隙.

盡管壓電材料的引入對聲子晶體帶隙的主動調控提供了新思路和新方法,但實現低頻寬帶隙的調控依舊是聲子晶體研究的難點之一.為了獲得好的帶隙特性,本文設計了一種由三組元材料構成的新型二維壓電聲子晶體板,利用有限元方法計算了該聲子晶體板能帶結構、傳輸損失以及位移場,研究了開路和短路兩種電邊界條件對能帶結構的影響,并分析了壓電常數對能帶結構的影響;對由電邊界條件缺陷構成的壓電聲子晶體板波導也進行了討論.

2 物理模型及方法

圖1(a)為二維壓電聲子晶體板的初基原胞示意圖,該結構由包裹有機玻璃涂層的圓柱形壓電材料按正方形晶格周期性連接在四個環氧樹脂短板上構成,x-y平面位于板的中間平面上,z軸沿著厚度方向.本文采用沿[001]方向極化且具有高機電耦合系數的壓電材料0.27PIN-0.4PMN-0.33PT作為散射體.聲子晶體板的結構參數定義如下:晶格常數為a,柱狀壓電散射體的半徑和高度分別為r1和h1,包裹層的半徑和高度分別為r2和h2,連接板的厚度和寬度分別用d和l表示.在以下計算中,壓電材料和彈性材料的參數分別由表1和表2列出.

圖1 (a)壓電聲子晶體板初基原胞;(b)第一布里淵區與不可約布里淵區Fig.1.(a)Unit cell of the investigated piezoelectric phononic crystal plate;(b)the corresponding first irreducible Brillouin zone of square lattice.

表1 壓電材料參數Table 1.Parameters of the piezoelectric material.

表2 彈性材料參數Table 2.Parameters of the elastic materials.

有限元法是隨著電子計算機的發展而迅速發展起來的一種現代計算方法,該方法不僅計算精度高,而且能適應各種復雜形狀,因而成為行之有效的工程分析手段.本文利用有限元軟件COMSOL MULTIPHYSICS[25]來求解周期結構的能帶色散關系和傳輸特性.基于有限元法的壓電控制方程為[22]

式中ρ,uj,t分別為密度、位移和時間;xi(i=1,2,3)分別對應坐標變量x,y和z;Tij和Di分別為應力和電位移,并遵守位移uj和電位φ作為變量的壓電本構關系[22]:

(3)和(4)式中,cijkl,elij和εil分別為彈性常數、壓電常數和介電常數.在壓電散射體的表面區域上,可應用電邊界條件來調整彈性波波速度.

考慮兩種類型的電邊界條件如下[26]:

1)如果表面是自由表面,則稱為開路狀態,表面上電位移的法向分量Dz=0;

2)如果表面被非常薄的金屬膜覆蓋并接地,則稱為短路狀態,表面上的電勢φ=0.

聲波速度取決于材料特性,例如壓電性,因此可以改變波速來調控色散關系.施加在壓電散射體表面上的導電金屬膜消除了切向電場,從而抑制了材料的壓電性.

在所提出的模型中,由于沿著x和y方向的周期性結構是無限的,所以在計算過程中只需要考慮圖1(a)中所示結構單元.因此,基于布洛赫定理,周期性邊界條件施加在單位元胞及其四個相鄰單元之間的邊界處[20]:

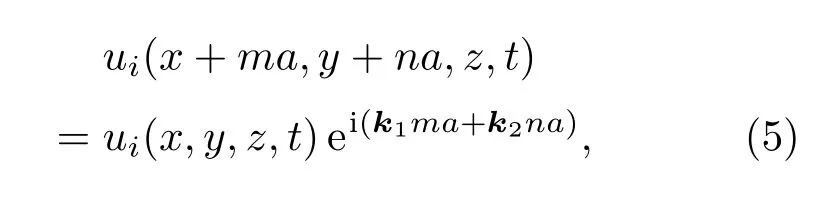
其中m和n是整數,并且k1和k2分別是x方向和y方向上的Bloch波向量的分量.通過改變第一布里淵區中的k1和k2的值并求解由有限元算法產生的特征值問題,即可獲得色散關系以及本征模.

此外,我們計算了彈性波在壓電聲子晶體板中的傳輸損失譜,以驗證色散關系的數值結果.圖2所示為計算傳輸損失時所采用的有限周期結構,該結構在x方向上由16個單元胞組成,在y方向上,布洛赫周期邊界條件仍然應用于兩個邊界代表無限系統的有限結構.在模擬過程中,位移激勵din施加在有限結構的左側,平均位移響應dout在結構的右側被拾取.傳輸損失T定義為

圖2 用于計算傳輸損失的有限系統Fig.2.Finite structure for the calculation of transmission loss.

3 結果與討論

3.1 不同電邊界條件下的能帶結構

為了研究提出的聲子晶體結構的帶隙特性,利用有限元方法對其能帶結構和傳輸損失進行了計算.能帶結構可通過在壓電材料表面施加不同的電邊界條件來調控,這里分別討論了開路和短路兩種電邊界條件對完全帶隙產生的影響.在計算中,幾何參數取值分別為:a=20 mm,r1=6.5 mm,h1=10 mm,r2=8 mm,h2=4 mm,l=5 mm,d=2 mm.圖3(a)—(d)給出了壓電聲子晶體板分別在開路和短路兩種不同電邊界條件下的能帶結構及傳輸損失譜,可以看出在傳輸損失中出現的衰減頻率范圍和能帶結構圖中的帶隙頻率范圍基本符合,這很好地驗證了能帶結構的數值結果.開路條件下,如圖3(b)所示,可觀察到頻率在0—2000 m/s(以頻率和晶格常數的乘積為單位)的范圍內有10個完全帶隙,前三個完全帶隙分別為199.5—766.4,810.8—830.9以及942—1054 m/s.圖3(c)為短路條件下的能帶結構,同樣可以觀察到10個完全帶隙,前三個完全帶隙分別為199.2—764.7,809.4—838.6和877.3—990.3 m/s;與圖3(b)相比,可以發現隨著電邊界條件的交替施加,第一和第二完全帶隙的邊緣幾乎保持不變,而在高頻范圍有多條完全帶隙發生了明顯的變化,這種顯著的差異表明,通過施加不同的電邊界條件,新型聲子晶體結構可以同時對多條完全帶隙進行主動調控.

為了進一步解釋電邊界條件對帶隙的影響,我們計算了不同頻率下的位移矢量場,如圖4所示.可以看出較低頻帶所對應的振動模式主要為壓電散射體的面內扭轉模式,其表面沒有發生形變,而高頻帶對應的振動模式主要為壓電散射體的彎曲振動,這使得壓電材料產生了壓電效應.因此,通過使用不同的電邊界條件,可以改變壓電聲子晶體板的頻帶間隙.利用這種可變特性,可以通過聲子晶體板表面上的電邊界條件來實現對不同頻率聲波能量流的控制.

作為對比,我們對Hsu[22]提出的由圓柱形壓電散射體周期性嵌入到均質薄板中構成的二元傳統聲子晶體板帶隙特性進行了計算,結果如圖5所示.可以觀察到圖5中出現了兩個完全帶隙,分別為978—1083和1214—1373 m/s.通過比較和分析,可以得出:具有周期性涂層及連接板結構的三組元壓電聲子晶體可以在相對較低的頻率范圍內獲得帶寬更大的完全帶隙,并在高頻范圍出現更多的完全帶隙.

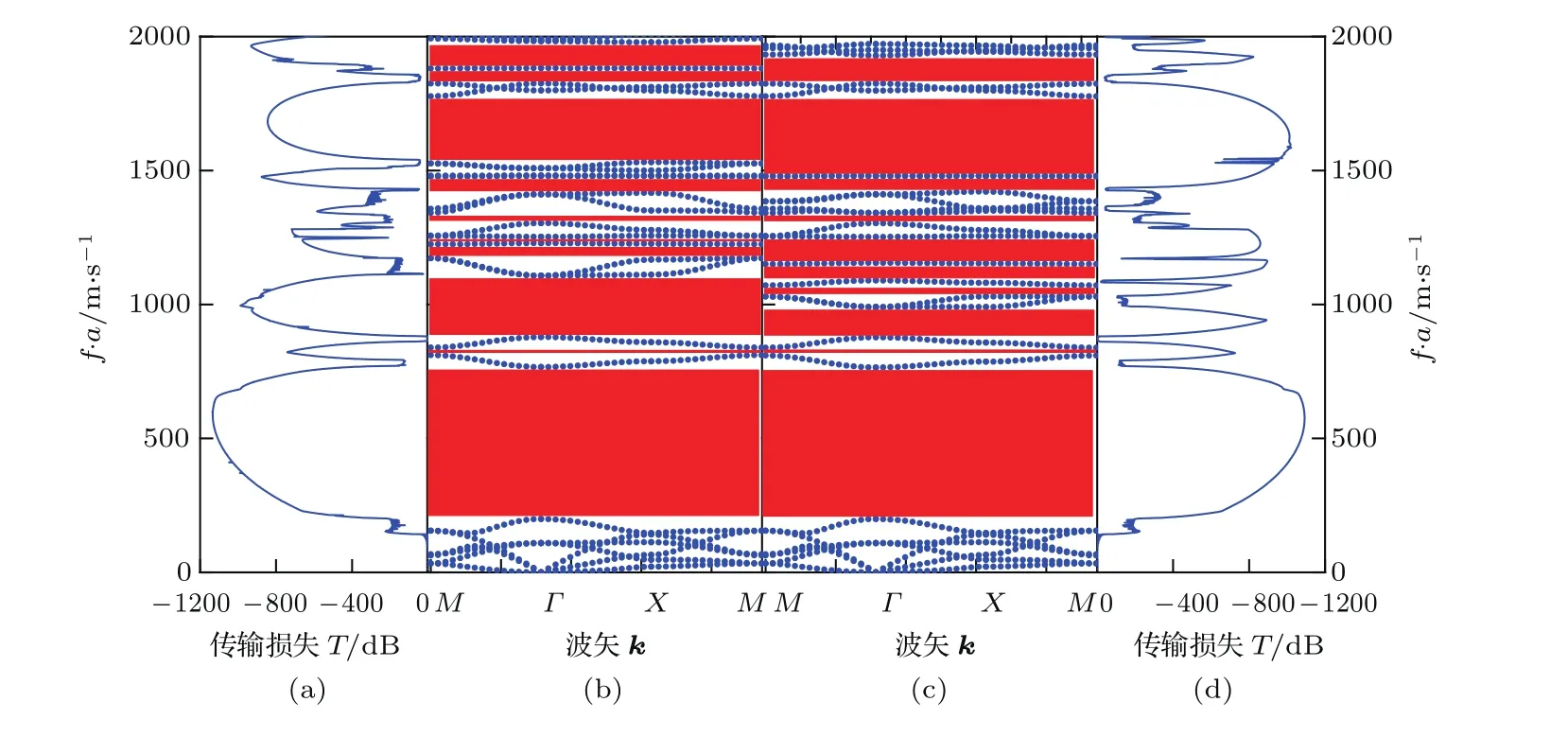
圖3 開路和短路電邊界條件下的能帶結構和傳輸損失譜 (a)和(b)開路電邊界條件;(c)和(d)短路電邊界條件Fig.3.Band Structures and transmission loss spectra with open and short electrical boundary conditions:(a),(b)Open-circuit conditions;(c),(d)short-circuit condition.

圖4 不同本征模對應的位移矢量場Fig.4.Eigenmode displacement fields of the different eigenmodes.

圖5 二組元傳統聲子晶體板及能帶結構示意圖Fig.5.Schematic diagrams of the binary phononic crystal plate and the band structure.

3.2 壓電效應對能帶結構的影響

壓電效應使得壓電材料的特性與彈性材料不同,壓電常數(e15,e31,e33)與電彈性耦合強度直接相關.接下來,將通過改變壓電常數來研究帶隙上的壓電效應.為此,新的壓電常數e′被定義為如果考慮真實的壓電材料屬性,設定e′/e=1,對于沒有壓電效應的情況,e′/e=0.圖6分別給出了具有壓電效應和不具有壓電效應時該新型二維壓電聲子晶體板的能帶結構,發現考慮壓電效應時,圖6(a)給出的能帶結構和圖3(b)相同;當壓電效應被忽略時,第一和第二完全帶隙的邊緣發生了微小的變化,帶隙寬度與考慮壓電效應時的帶隙寬度基本相同,而高頻完全帶隙發生了明顯的變化,如圖6(b)所示.為了進一步揭示壓電效應對帶隙的影響規律,將壓電常數e′/e從0(無壓電)逐漸改變為1(實際值).圖7所示為第三和第四完全帶隙邊緣隨壓電常數的變化情況,可以看出,隨著壓電常數逐漸增加,第三完全帶隙的下邊緣幾乎保持不變,帶隙的上邊緣隨著耦合強度的增加而上移,從而使得帶隙的寬度逐漸變寬;第四完全帶隙的上下邊緣均隨著壓電常數的增大而向上移動.因此,可以得出:壓電效應對完全帶隙有顯著影響,受壓電效應影響的頻帶會隨著壓電常數的增大向上移動,這有利于完全帶隙的擴大和形成.

圖6 壓電聲子晶體板能帶結構 (a)有壓電效應;(b)無壓電效應Fig.6.Band structures of the piezoelectric phononic crystal slab(a)with piezoelectric effect and(b)without piezoelectric effect.

圖7 壓電常數e′對第三和第四完全帶隙上邊緣和下邊緣的影響Fig.7.Effects of the piezoelectric constant e′on the upper and lower edges of the third and fourth complete bandgaps.

3.3 壓電聲子晶體板的缺陷模式

前面已經證明了通過改變電邊界條件可以有效調控壓電聲子晶體板中的完全帶隙,基于該結果,本節旨在設計出可切換路徑的二維聲子晶體波導.圖8(a)給出了具有電邊界缺陷的聲子晶體板能帶結構,這里通過將一個壓電散射體的開路電邊界條件替換為短路來形成電邊界缺陷,如圖8(a)中內插圖所示.采用超晶胞方法模擬無限長壓電聲子晶體板波導并計算其能帶結構,計算中采用的超晶胞含有五個單位元胞,Bloch周期性邊界條件施加在四個邊界上,并將波矢k沿著Γ—X方向掃描得到該方向的能帶結構.將圖8(a)和圖3(b)進行對比,可以看到在950—1100 m/s之間存在三個頻散曲線(即缺陷頻帶).圖8(b)給出了三種不同缺陷模式的總位移場,它們相應的頻率分別與圖8(a)中的標記點一一對應.模式A—C是良好導向模式,其彈性能量主要限制在電邊界缺陷(即短路區域)附近.隨著短路條件的施加,壓電散射體的有效彈性剛度因消除切向電場而減小,因此可以將彈性波限制在點缺陷周圍.與圖8(b)所示的其他缺陷模式相比,模式C的振動局域在短路條件的壓電散射體中,更強烈地限制在缺陷處.

圖8 (a)由電邊界缺陷產生的壓電聲子晶體板波導的能帶結構;(b)壓電聲子晶體板波導的幾種缺陷模式Fig.8.(a)Band structure for the piezoelectric phononic crystal slab waveguide produced by electrical boundary defects and(b)several defect modes of the piezoelectric phononic crystal slab waveguide.

圖9為缺陷聲子晶體板和完美聲子晶體板的傳輸損失譜對比示意圖.在0—1150 m/s范圍內,完美聲子晶體板傳輸損失譜有三個明顯的能量衰減區域,能量衰減的頻率范圍分別為200—769,810—831以及940—1055 m/s,這與圖3(b)中的帶隙頻率范圍對應一致.當引入線缺陷時,第一和第二完全帶隙的頻率范圍幾乎保持不變,而在1023 m/s附近出現峰值,表明峰值是由于缺陷造成的.

圖9 彈性波在由5×1超晶胞構成的有限陣列結構中沿x方向傳播的透射譜示意圖Fig.9.Schematics of the transmission spectra of a finite array structure composed of 5×1 supercell for elastic waves propagating along x direction.

4 結 論

在聲子晶體中引入壓電材料,利用對壓電效應的控制改變聲子晶體中壓電組元的材料參數,形成可調帶隙聲子晶體,可以克服聲子晶體結構在材料參數及結構參數確定后帶隙不可變的局限性,以適應不同振動環境下的減振降噪需求.本文利用有限元法詳細計算了所設計的由包裹有機玻璃涂層的圓柱形壓電材料按正方形晶格周期性連接在四個環氧樹脂短板上構成的新型二維壓電聲子晶體板的能帶結構、傳輸損失譜及位移場.結果表明:與二組元的傳統聲子晶體板相比,這種新型周期結構可以在較低頻率范圍內獲得更寬的完全帶隙,帶隙寬度擴大了5倍;通過改變施加在壓電散射體上下表面的電邊界條件,可以同時對多條完全帶隙進行調控,可實現對完全帶隙的主動控制;壓電效應對能帶結構影響很大,比較分析發現壓電效應有利于完全帶隙的擴大和產生.此外,對電邊界缺陷形成的二維聲子晶體板波導進行了研究,結果表明電邊界缺陷可能導致完全帶隙中存在多條缺陷頻帶,利用電邊界條件的轉換可以實現對不同頻率彈性波傳播的主動控制.本工作所研究內容能夠為主動控制傳輸、引導、切換和發射彈性波的聲子晶體結構設計提供有價值的參考.