渦扇發動機軸向定位彈性環優化設計

盧玲玲，于進學

(中國航發四川燃氣渦輪研究院，成都 610500)

1 引言

彈性元件在航空發動機中的應用非常廣泛[1]，主要位于各軸承處，用于調節支點剛度。某型發動機的軸向彈性環安裝于4#支點的軸承前端，起軸承內環軸向定位作用。該發動機在試驗后分解發現，4#軸承內環與軸之間存在周向劃痕，彈性環存在約0.080 mm的軸向殘余變形。通過分析，推斷引起該問題的主要原因為：軸向彈性環使用過程中產生的軸向殘余變形太大，導致軸承內環工作時軸向定位不可靠，在軸承的作用下發生周向轉動。

本文針對該彈性環塑性變形問題，采用有限元法對軸向彈性環進行了應力及變形分析，解釋并驗證了彈性環的殘余變形。在此基礎上，用力學解析法對彈性環結構參數進行優化，得出影響彈性環強度和剛度的三個主要因素(支反力、材料屬性及結構參數)。最后根據發動機空間結構及相關需求，在保證一定支反力的情況下確定了優化方案，解決了彈性環在使用過程中軸向殘余變形過大的問題。

2 彈性環強度分析

2.1 結構參數

軸向彈性環在發動機上的裝配及三維實體結構示意見圖1，結構參數見表1。彈性環材料為1Cr11Ni2W2MoV[2]。初始裝配時，彈性環的軸向壓緊量為0.200 mm。

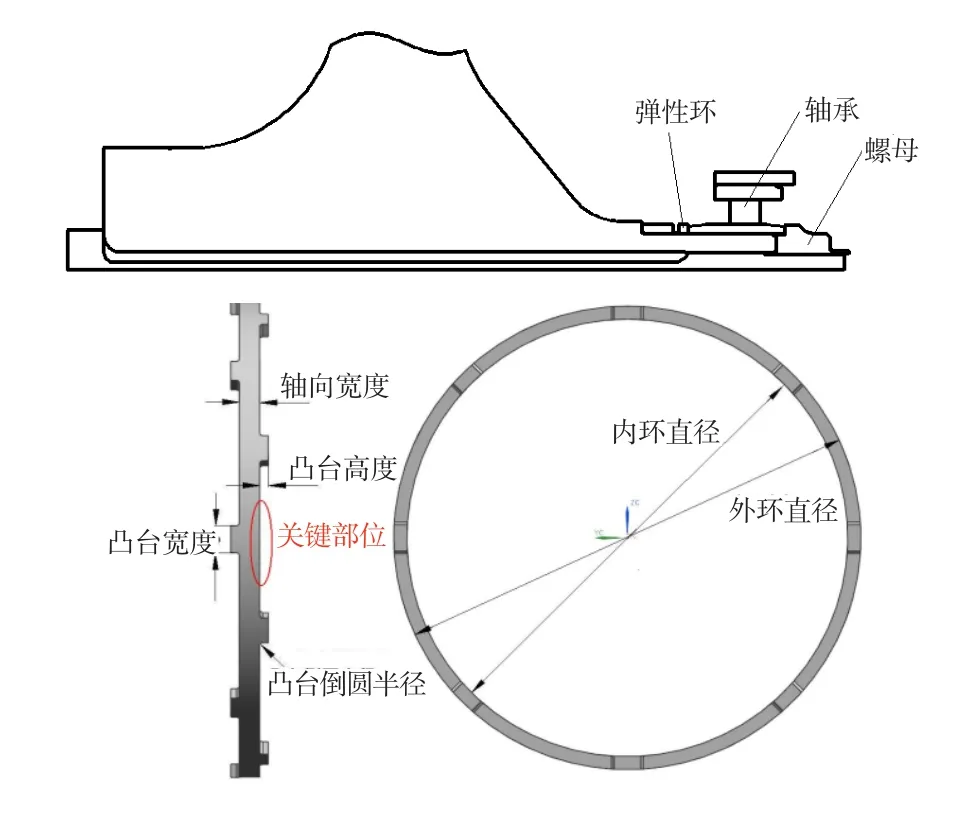
圖1 軸向彈性環裝配及實體結構示意圖Fig.1 Assembly and structure schematic of an axial elastic ring

表1 軸向彈性環原始結構參數Table 1 Original structural parameters of an axial elastic ring

2.2 有限元模型

以整圈彈性環作為計算模型采用帶中節點的六面體單元劃分網格。圖2為彈性環有限元模型。

圖2 彈性環有限元模型Fig.2 Finite element model of an axial elastic ring

2.3 靜強度結果分析

2.3.1 彈性計算

在彈性環兩側分別建立剛性面，8個凸臺端面與剛性面接觸，強度計算時固支其中一側剛性面的自由度，另一側剛性面施加0.200 mm的軸向強迫位移。圖3為彈性環等效應力分布，圖4為彈性環第一主應力分布。由3和圖4可看出，彈性環凸臺倒圓處主要為壓應力，凸臺背部主要為拉應力，且均超過材料的屈服極限，需對其進行結構優化。由圖5可知，在0.200 mm強迫位移下，彈性環大面積進入了屈服階段，需對其進行彈塑性分析。圖6給出了彈性環軸向變形分布。

圖3 彈性環等效應力分布Fig.3 Equivalent stress distribution of an axial elastic ring

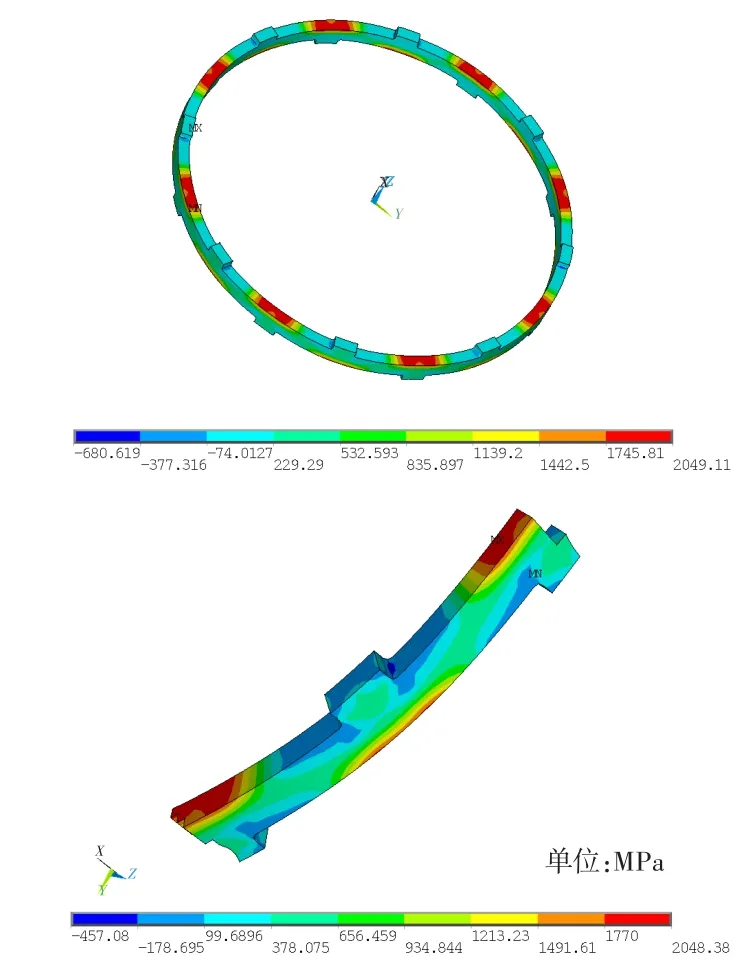
圖4 彈性環第一主應力分布Fig.4 First principal stress of an axial elastic ring

2.3.2 彈塑性計算

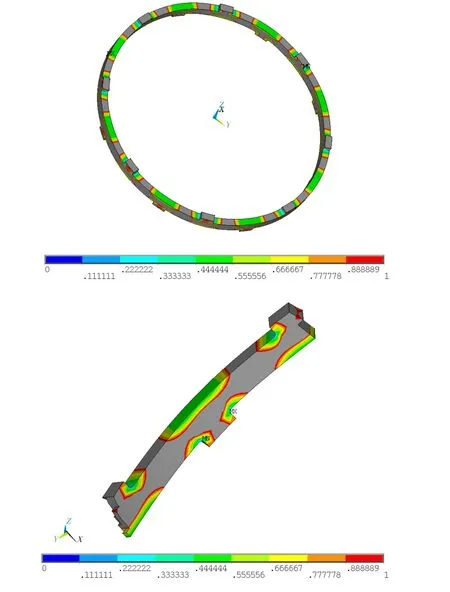
圖5 彈性環屈服強度儲備分布Fig.5 Yield strength reserve distribution of an axial elastic ring

圖6 彈性環軸向變形分布Fig.6 Axial deformation distribution of an axial elastic ring

由于彈性環凸臺根部倒圓、凸臺背部較大區域進入屈服，且應力較高，影響了支反力計算的準確性，同時也為分析其使用后的殘余變形，進行了彈塑性計算分析。分析時，分兩個載荷步：第一步加載，固支彈性環一側剛性面的自由度，另一側剛性面施加0.200 mm的軸向強迫位移邊界；第二步卸載，固支彈性環一側剛性面的自由度，另一側剛性面自由邊界。圖7為彈性環軸向殘余變形分布。由圖可知，卸載后彈性環的殘余變形量約為0.064 mm。彈性環實際使用分解后的殘余變形量約為0.080 mm，有限元計算結果與實際情況基本相符。在0.200 mm壓縮量下，彈性環大部分區域產生了塑性變形，需要對彈性環的結構進行優化設計。圖8給出了彈性環塑性應變分布。

3 彈性環優化設計

3.1 解析法參數分析

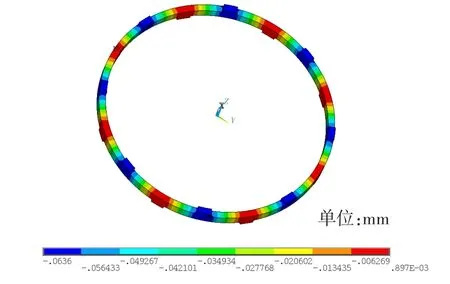
圖7 彈性環殘余變形分布Fig.7 Residual deformation distributionof an axial elastic ring

圖8 彈性環塑性應變分布Fig.8 Plastic strain distribution of an axial elastic ring

由于彈性環是循環對稱結構，為便于分析，取1/8的彈性環近似簡化成簡支梁，見圖9。彈性環的軸向寬度為a，徑向厚度為b，簡支梁的長度為L。

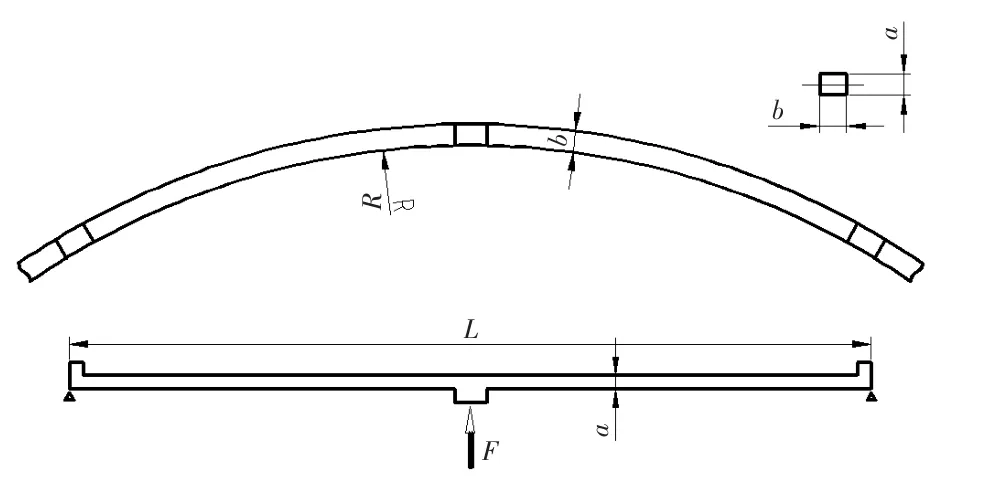
圖9 軸向彈性環結構簡化示意圖Fig.9 Simplified schematic diagram of an axial elastic ring structure

簡支梁的撓度[3]為：

式中：F為彈性環所受的壓力(本文與支反力相反），E為彈性模量，I為抗彎模量。

最大彎曲截面的應力為：

彈性環的屈服強度儲備系數為：

彈性環的剛度為[4]：

彈性環結構在使用后產生了較大塑性變形，需要提高其關鍵部位的屈服強度儲備系數。另外，為保證彈性環的定位作用及裝配精度，彈性環剛度應保持不變或降低。為此，需增大彈性環的屈服儲備系數與剛度的比值。根據公式(1)～(4)，可得：

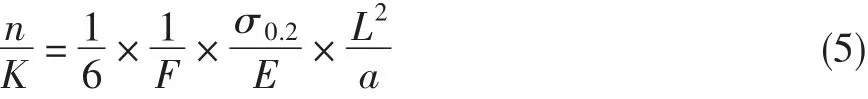
3.2 優化方案分析

根據彈性環加工、裝配要求以及使用特點，確定其結構優化指標如下：①為保證裝配可靠，彈性環壓縮量不低于0.150 mm；②為保證軸承內環的定位可靠，彈性環的支反力為7 000～9 000 N；③為保證加工質量，彈性環軸向寬度應不小于1.200 mm；④受結構空間限制，彈性環內外環直徑保持不變，總軸向寬度不大于3.600 mm。

根據上述優化原則及剛度、強度影響因素分析結果，確定彈性環優化方向為：①材料優化——選擇材料性能更好(更高)的材料。②載荷優化——彈性環壓縮量從原來的0.200 mm降低至0.150 mm，增大項。③結構優化——考慮到彈性環傳遞軸向力均勻、軸承內環定位可靠等問題，優化后彈性環凸臺數最終確定為8個，與原結構保持一致；為降低凸臺倒圓處的應力集中，增大凸臺倒圓半徑；通過減小彈性環的軸向寬度，增大項的值。

3.3 材料優化

航空發動機常使用1Cr11Ni2W2MoV、GH4169[5]以及GH145等作為彈性元件的材料，分別對這3種材料彈性環的屈服強度與彈性模量比值進行對比分析，結果見表2。從表中可看出，GH4169材料的項值最大，更適合作為彈性環的材料。

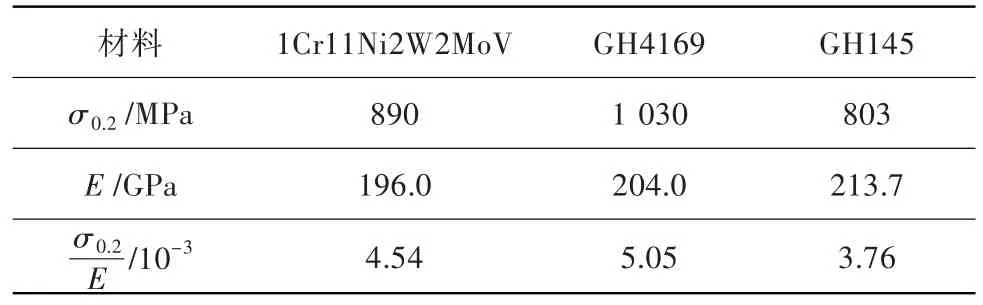
表2 材料性能對比Table 2 Comparison of material properties

3.4 載荷優化

由于受空間限制，彈性環很薄，為保證裝配及強度可靠，彈性環壓縮量從原來的0.200 mm降至0.150 mm，從而使得彈性環載荷降低，提高了彈性環的強度儲備。

3.5 結構優化

基于彈性環材料為GH4169，通過調整軸向寬度對彈性環進行進一步的優化設計，表3給出了彈性環各優化方案的結構參數。經分析，凸臺倒圓半徑對應力的影響不大，但增大可以增加凸臺背部的剛性，結構優化時將凸臺的倒圓半徑增大為5.000 mm。

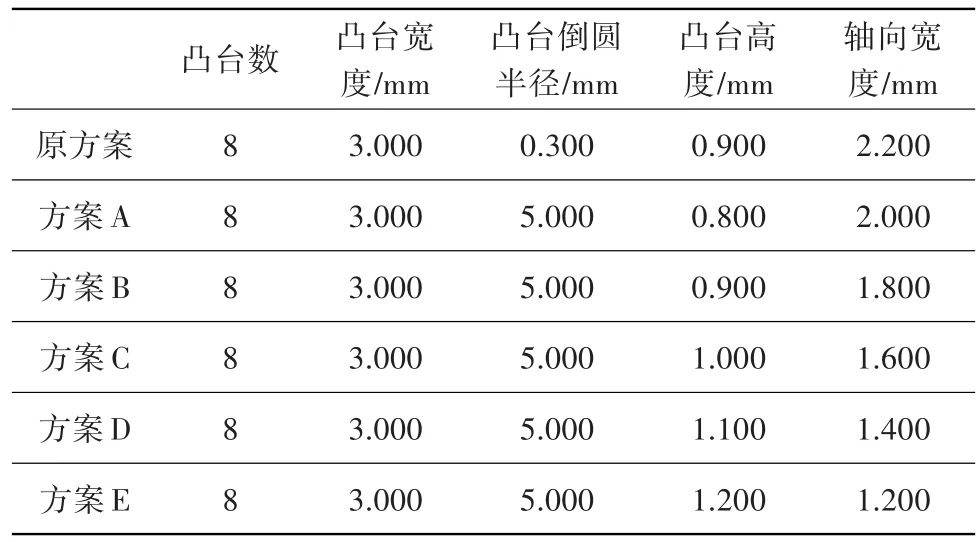
表3 各方案結構參數Table 3 Structural parameters of various concepts

在0.150 mm強迫位移邊界下，彈性環各優化方案的彈性計算結果見表4。可看出，方案A、方案B以及原結構方案關鍵部位屈服儲備最低，且擠壓面的支反力大于9 000 N，不滿足使用要求；方案E強度儲備最高，但支反力低于7 000 N，也不滿足使用要求；方案C、方案D支反力滿足7 000～9 000 N的要求，關鍵部位屈服儲備相當。考慮到彈性環的加工質量和裝配定位可靠，選擇軸向寬度和支反力相對較大的方案C為最終優化方案。

表4 彈性計算結果Table 4 Elastic calculation results

3.6 優化方案彈塑性分析

由于彈性環優化方案C關鍵部位局部進入屈服，為分析其殘余變形，對其進行了彈塑性分析。圖10為殘余變形分布，圖11為彈性環塑性應變分布。計算分析得到，優化方案C在0.150 mm的軸向壓縮量下，擠壓面的支反力為7 850 N，滿足使用要求；彈性環塑性應變從原狀態最大塑性應變0.025降低為0.002，優化后彈性環在0.150 mm的壓縮量下會發生0.006 mm的軸向殘余變形，優化后彈性環的殘余變形量明顯降低。

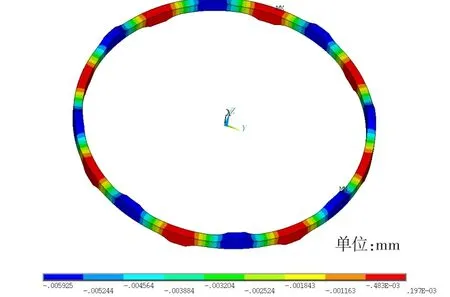
圖10 優化后的殘余變形分布Fig.1 0 Residual distribution after optimization

4 試驗驗證

發動機采用優化后的軸向彈性環后，經多次試驗分解，4#軸承內環未發現周向劃痕，彈性環無明顯殘余變形。這證明優化后的軸向彈性環能起到軸向壓緊軸承內環的作用，滿足發動機的使用要求。

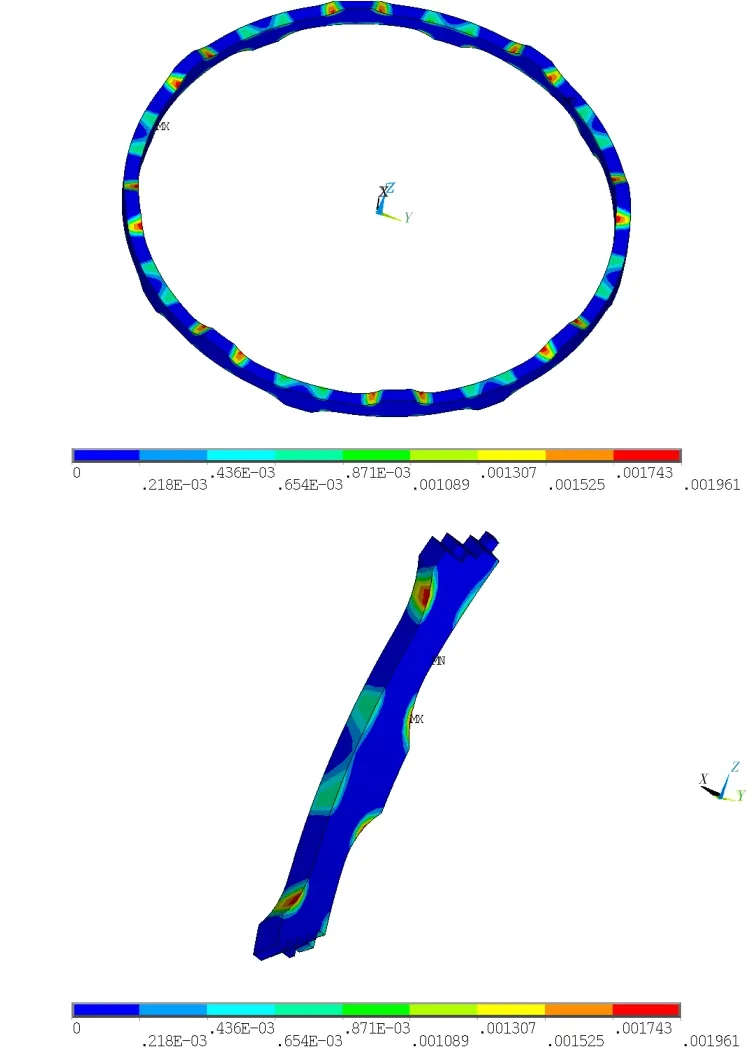
圖11 優化后的塑性應變分布Fig.1 1 Plastic strain distribution after optimization

5 結論

針對渦扇發動機4#支點處的軸向彈性環存在較大的殘余變形導致的軸向定位不可靠問題，通過力學解析以及有限元法，對材料、載荷以及結構進行優化，確定了合理的優化方案，使軸向彈性環滿足發動機使用要求，解決了工程實際問題。對于彈性環的結構優化，文中根據其結構及承載特點，提出的優化目標函數能夠高效地定位優化方向和關鍵參數，快速獲得最佳優化參數，可為其他類似彈性環的優化提供參考。