一種采用遺傳算法優化離心葉輪結構的方法

陳鼎欣，銀越千，鄔國凡

(中國航發湖南動力機械研究所，湖南 株洲 412002)

1 引言

隨著高功重比航空發動機的發展，以犧牲發動機油耗、機動等特性為代價，單純通過增加結構材料提高關鍵零部件強度和可靠性，已難以滿足先進發動機的研制需要。離心葉輪作為大多數中小型航空發動機的核心轉子件，其結構性能的優劣直接影響整個航空發動機的功能實現[1]。如何通過多目標優化的方法改善離心葉輪的結構性能，提高結構質量的利用率，成為許多專家學者關注的課題[2-9]。蔡顯新等[2]運用改進的耦合分析數學模型對葉輪應力分布進行了優化，陸山等[3]通過二維、三維方法對整體葉片盤進行了以改善應力分布為目的的分步優化，雒婧等[4]通過對離心葉輪葉輪背結構特征參數進行優化減小了離心葉輪的應力集中程度。然而，由于傳統多目標優化的局限性，這些研究往往集中于局部特征優化，難以實現結構的全面最優設計。

遺傳算法基于生物進化原理搜索最優解，在整個解群體中不斷自適應地進行隨機搜索，具有內在的隱并行性和更好的全局尋優能力，引入遺傳算法一定程度上能克服單純利用數值計算處理多目標優化問題的局限。劉小民等[5]運用遺傳算法對離心葉輪葉片結構進行了優化設計，張明輝等[6]運用神經網絡與遺傳算法對離心葉輪全局優化進行了部分理論研究。不過在全面考慮設計參數特點的基礎上，綜合采用數值擬合與遺傳算法對離心葉輪結構參數進行全局優化的相關研究還較少。

本文以結構質量與結構應力指標為優化目標，提出一種基于代理模型-遺傳算法的離心葉輪結構設計參數全面優化方法。主要包括利用拉丁超立方試驗設計方法獲取樣本數據，運用Kriging近似模型構造覆蓋整個設計參數范圍的響應面，以遺傳算法對多目標參數響應面的高適應度區域尋優；采用整體到局部的多目標優化步驟，實現結構的優化設計；通過不同狀態離心葉輪結構強度的對比分析，驗證結構優化設計的有效性。

2 結構優化方法

對于離心葉輪結構優化問題，若確定結構質量最小作為主要目標，對于其他如應力、變形等目標函數只要滿足一定限制條件，即可把這些函數當作約束來處理[10]，從而將多目標優化問題表示為如下數學模型：

式中：X為設計變量，離心葉輪質量m為目標函數，Xs、Xt分別為設計變量的上、下限，vi(X)為約束函數。

為獲取離心葉輪結構的全局優化結果，采用代理模型-遺傳算法進行多目標優化。代理模型的確定包括獲取試驗設計樣本和以樣本數據為前提的數值模型替代[11]。通過合理選擇代理模型構造響應面不僅能減小問題的非線性，也能有效減少對真實問題再現的計算量，提高遺傳算法的效率。代理模型-遺傳算法結構參數優化流程如圖1所示，具體過程如下：

(1)根據待優化離心葉輪的結構特點設計初步結構優化方案，確定作為設計變量的輸入參數，以及作為目標函數的輸出參數。

(2)運用試驗設計方法與強度計算模塊，獲得設計變量與響應的樣本數據集合。

(3)通過樣本數據點構造代理模型的響應面，并對響應面進行遺傳算法尋優，形成基于代理模型的預測最優解F1。

(4)將預測最優解點的設計參數代入進行強度計算，獲得目標實際解F2。由于代理模型是通過真實數據構造，故可認為遺傳算法尋優的響應面是真實情況的函數替代。公式(1)通過相對誤差E判斷優化解是否可信。若不可信，說明構造的響應面與真實情況存在過大誤差，需提高響應面精度；預測可信，即可認為對真實情況進行了有效替代，代理模型-遺傳算法優化結果有效。

圖1 結構優化流程Fig.1 Structure optimization process

3 離心葉輪結構優化

待優化離心葉輪為某型離心葉輪的方案設計結構，其材料為鍛件TC11鈦合金(強度性能見表1)。以輪盤最高工作溫度260℃為屈服強度評價溫度，插值獲得其屈服強度為768.5 MPa。設計轉速為49 000 r/min。離心葉輪前端施加78 400 N預緊力，后端面施加軸向和周向的位移約束。由于氣動力對輪盤強度的影響相對較小，故文中不予考慮。輪盤強度評價采用EGD-3的標準[12]，即最大當量應力σmax不大于屈服極限σ0.2，最大徑向應力σrmax不大于80%的屈服極限，最大周向應力σθmax不大于95%的屈服極限。

表1 TC11性能參數Table 1 TC11 performance parameters

3.1 結構方案初步設計

離心葉輪結構初步優化方案輪廓及具體待優化參數如圖2所示，初步優化參數的確定充分參考了以往設計經驗并結合了其輪盤結構具體特點。

圖2 參數化優化結構Fig.2 Parameterized optimization structure

運用ANSYS對初始模型及初步優化的參數模型進行穩態熱力學與結構力學聯合計算，并由此構造輸入設計變量運行計算、提取結構質量與最大應力值為輸出參數的強度計算模塊。由圖3中的當量應力分布可看出，初始結構的當量應力最大值在輪心邊緣位置，初步優化結構的最大當量應力接近盤心中部，雖然其值有一定增加，但較大應力分布區更大，且其最大徑向和周向應力均有一定程度減小。表2給出了最大應力及質量對比。由以上結果可知，本文提出的結構初步優化方案較合理，能有效優化離心葉輪的應力分布，并減小結構質量。初步優化方案的最大應力均有較大裕度，故可在強度限制條件下對結構參數進行多目標優化，以實現離心葉輪結構的全局最優設計。

3.2 結構參數整體優化

根據離心葉輪初步優化方案，選取整體多目標各參數。

圖3 初始結構與初步優化結構應力Fig.3 Structural stress of initial structure and initial optimization

表2 初步計算結果對比Table 2 Comparison of preliminary calculation results

目標約束：σmax≤768.5 MPa，σrmax≤614.5 MPa，σθmax≤730.1MPa。

目標函數：m最小。

設計變量尋優范圍充分考慮了去料最大化與優化結構合理性。由于拉丁超立方設計在樣本空間取值的均勻分散性、取值分布隨機性及充分覆蓋設計空間的全面性，適合多參數、大采樣空間取樣[11]，因此文中選擇拉丁超立方試驗設計獲取設計變量范圍內的全局樣本數據。

按圖1流程，通過試驗設計選取90組參數樣本并調用強度計算模塊獲得每組樣本的質量與目標應力，運用代理模型構造樣本數據的響應面。因Kriging代理模型具有相對更好的擬合平滑性和統計學的方差最小特征，以及對高維度問題更好的適應性[11]，故文中選擇該模型對樣本數據進行擬合。

通過遺傳算法內部尋優機制捕捉響應最優點，形成與預測點對應的強度模塊提取結果的對比條件判斷。式(1)中遺傳算法預測可信條件取e=1%，不可信則返回計算數據加入樣本數據集以提高最優區域響應面精度，可信即取強度計算結果為最終優化目標結果。

圖4為相對誤差隨迭代次數的變化。由圖可知，影響優化結果收斂的主要原因是最大徑向與周向應力的預測誤差，可能是由于這兩項應力指標在結構優化過程中存在位置轉換導致。經28次迭代，遺傳算法預測結果滿足收斂條件，獲得的優化參數結果見表3；判斷優化解收斂時，最優解下的遺傳算法預測結果與強度計算結果對比見表4。

圖4 相對誤差的變化趨勢Fig.4 Relative deviation trend

表3 設計變量優化的取值Table 3 Optimization value of design variable

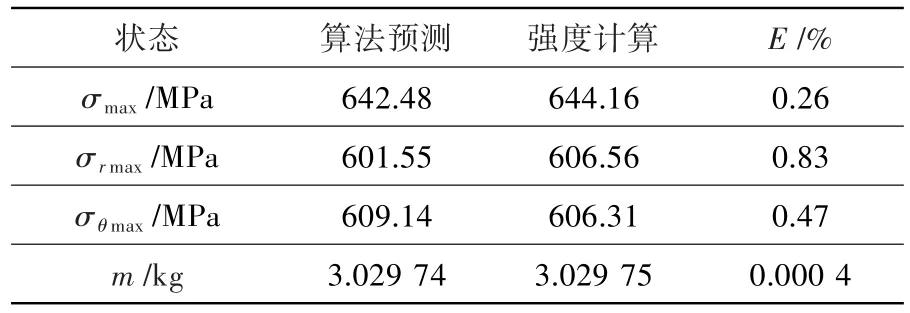
表4 整體優化結果對比Table 4 Comparison of the overall optimization results

對比表4與表2結果可知，通過代理模型-遺傳算法優化，離心葉輪質量明顯減小，相對于初步優化結構，整體優化后離心葉輪總質量減小約6.3%，結構的最大徑向和周向應力值有一定增加，但均控制在強度約束條件內。

3.3 局部結構再優化

以整體優化后的結構參數為設計變量，將參數偏移±5%作為變量約束，通過取樣和擬合，可獲得在以上求得的最優解區域基于Kriging代理模型的目標函數對各設計變量的局部靈敏度，如圖5所示。局部靈敏度反映了引起響應變化的輸入變量的權重，正、負值分別表示正、負相關。可見，經整體優化后仍然存在局部參數對目標值影響較大的情況，故有必要選取局部靈敏度相對較高的 A3、L3、L4為設計變量，其余參數均取已求得的優化值，再次運用圖1所示流程進行結構局部優化。

圖5 整體優化最優解點的局部靈敏度Fig.5 The local sensitivity of optimal solution point in overall optimization

局部優化范圍及結果見表5，最優點對應的優化目標函數預測及計算值見表6。對比可知，經局部參數優化，當量應力小幅增加，結構質量在整體優化基礎上減小了近2.0%。可見，合理選擇局部優化參數有效實現了結構再優化。

表5 局部變量優化的取值Table 5 Optimization value of local variable

表6 局部優化結果對比Table 6 Comparison of local optimization results

圖6 離心葉輪優化結構當量應力分布Fig.6 Centrifugal impeller equivalent stress distribution

離心葉輪優化后的當量應力分布如圖6所示。可見，相對于初步優化結構和整體優化結構，最終優化進一步提高了原低應力區域的應力水平，有效改善了離心葉輪應力分布不均。各階段優化結構外形對比如圖7所示。

圖7 優化前后結構對比Fig.7 The structure comparison before and after optimization

3.4 優化結果評價

引入平均應力值來衡量結構對質量的利用程度：

式中：σi、mi分別為不同節點位置的應力和質量。

由式(2)計算可得，初始結構、初步優化結構、整體優化結構、最終優化結構的平均應力值，分別為156.43、171.95、184.22、191.63 MPa，可見優化結構的平均承力明顯提高。圖8為四種結構不同應力范圍的質量分數對比，可見結構優化減少了結構在200 MPa以下低應力區的質量分數，提高了高應力區質量分數。遺傳算法優化顯著提高了300 MPa至500 MPa質量分數，由初步優化結構的7.2%，增加到整體優化及最終優化結構的12.9%與15.4%。由此可知結構優化通過增加較大應力區比例，提高了結構的利用效率，其中通過整體-局部優化流程的提高效果更為顯著。

圖8 不同應力范圍的質量分數Fig.8 Mass fraction of different stress ranges

另選取對壓氣機性能和結構布局影響較大的大葉片葉尖變形作為評價依據，根據結構優化前后其葉尖變形的變化量衡量其結構優化的可靠程度[8]。引入平均變形量：

式中：Di為葉尖某節點變形量，n為葉尖提取線上總節點數。

葉尖平均變形量Davg越小，葉片工作狀態與設計狀態差異越小，越有利于氣動狀態的穩定及氣動效率的提高。圖9為葉尖的總變形量的軸向分布(以順氣流方向為正)。由葉尖變形變化的趨勢分析可知，結構優化后葉尖總的變形量在流道進口區域得到顯著控制，初步優化結構、整體優化結構和最終優化結構最大相對減小，分別約為23.3%、46.6%和61.3%；流道中部區域變形量隨優化的進行有一定增大，至葉尖出口區域又趨于一致，結構優化對葉尖出口變形影響不明顯。通過式(3)進一步求得初始結構、初步優化結構、整體優化結構及最終優化結構的平均變形量，分別為0.44、0.40、0.37、0.36 mm，可見結構優化有效減小了離心葉輪葉片變形的程度。因此，在控制葉尖間隙確保安全的前提下，結構優化尤其是代理模型-遺傳算法優化同時也有助于減小離心葉輪葉尖平均變形量，一定程度上提高離心葉輪整體的可靠性。

圖9 葉尖總變形對比Fig.9 Comparison of the total blade tip deformation

4 結論

(1)在減重設計中對離心葉輪進行結構優化，不僅能有效減輕輪盤質量，也能使輪盤應力分布得到優化。

(2)運用代理模型-遺傳算法對輪盤結構參數進行多目標分步優化，能有效提高離心葉輪結構的利用率。針對本文算例，整體優化結構相對初步優化結構總質量減小約6.3%，局部優化在此基礎上還可再減小約2.0%。

(3)通過代理模型-遺傳算法結構優化，離心葉輪葉尖的區域變形量得到有效控制，有助于離心葉輪整體可靠性的提高。