方差與數據的穩定性

馬兆兵

蘇科版《數學》九年級上冊117頁的第3題是這樣描述的：

要從甲、乙兩名運動員中選出一名參加校際100m比賽，對這兩名運動員進行了10次測試，成績如下（單位：s）：

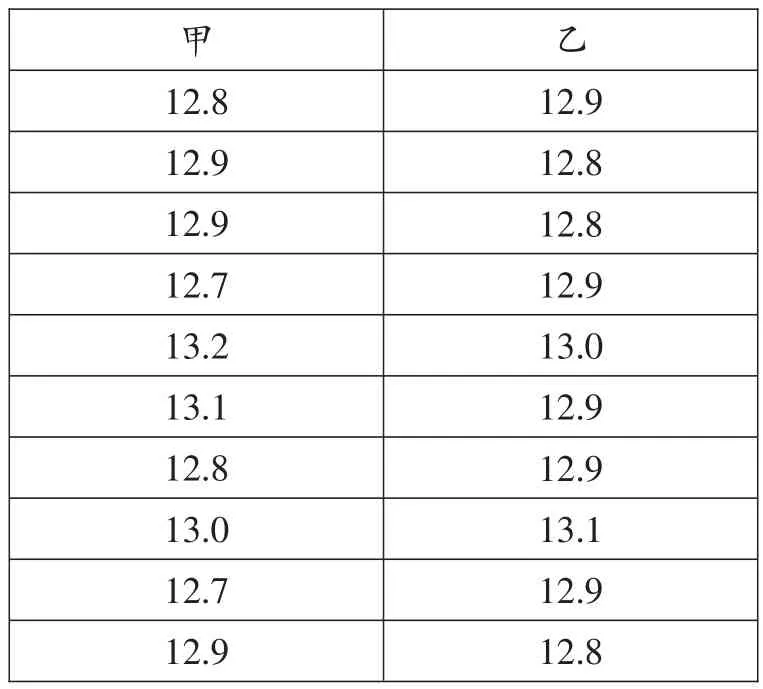
12.9 12.8 12.8 12.9 13.0 12.9 12.9 13.1 12.9 12.8甲乙12.8 12.9 12.9 12.7 13.2 13.1 12.8 13.0 12.7 12.9

根據測試成績，你認為選派哪一名運動員參賽更好些？為什么？

兩名運動員的平均成績都是12.9s，此時可通過計算兩組數據的方差來比較他們的穩定性.甲的方差為0.024，乙的方差為0.008，則選擇乙參加比賽.顯然，方差刻畫一組數據的離散程度（穩定性）.

一、用方差判斷一組數據的穩定性

例1甲、乙兩種水稻試驗品種連續5年的平均單位面積產量如下（單位：噸/公頃）：

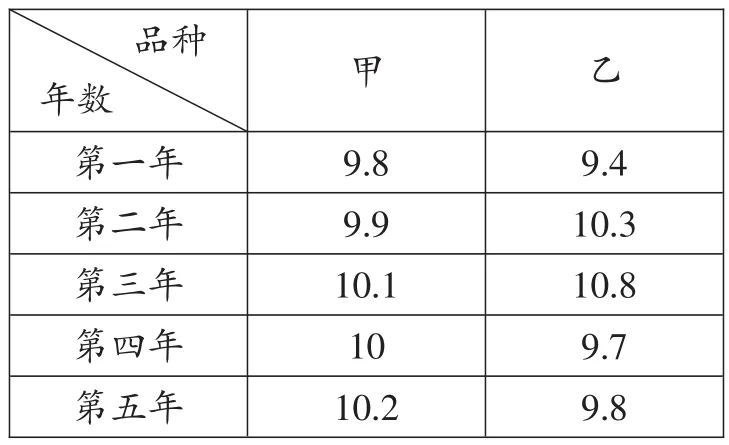
9.4 10.3 10.8 9.7 9.8品種年數甲乙第一年第二年第三年第四年第五年9.8 9.9 10.1 10 10.2

經計算，x甲=10噸/公頃，x乙=10噸/公頃，試根據這組數據估計________種水稻品種的產量比較穩定.

【解析】甲種水稻產量的方差是：

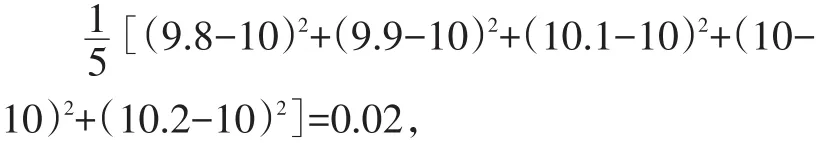
乙種水稻產量的方差是：

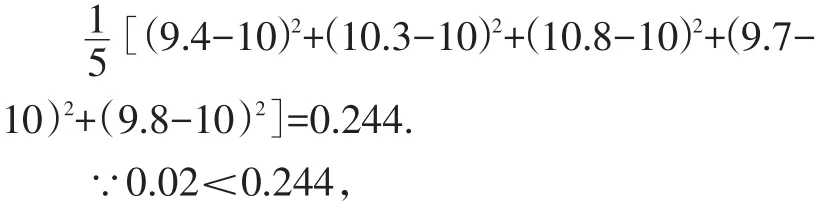
∴甲種水稻品種的產量比較穩定.

【點評】1.比較兩組數據的穩定性的步驟：

（1）計算這兩組數據的平均數.

（2）分別計算各自方差：s2=［（x1-x）2+（x2-x）2+…+（xn-x）2］.

（3）一組數據的方差越大，說明這組數據的離散程度越大；一組數據的方差越小，說明這組數據的離散程度越小.

2.比較一組數據的穩定性需要注意的問題：

一般情況下，兩組數據只有在平均數相同的情況下才根據方差的大小確定它們的離散程度.

二、利用圖表解決數據穩定性的問題

例2 為了從甲、乙兩名選手中選拔一人參加射擊比賽，現對他們進行一次測驗，兩個人在相同條件下各射靶10次，為了比較兩人的成績，制作了如下統計圖表：

甲、乙兩人的射擊成績統計表

（1）請補全上述圖表（請直接在表中填空和補全折線圖）.

（2）如果規定成績較穩定者勝出，你認為誰應勝出？說明你的理由.

（3）如果希望（2）中的另一名選手勝出，根據圖表中的信息，應該制定怎樣的評判規則？為什么？

【解析】（1）根據折線統計圖，得甲的射擊成績為（去掉第八次的成績）9，6，7，6，2，7，7，8，9，平均數為7環.

則甲第八次射擊成績為：

70-（9+6+7+6+2+7+7+8+9）=9（環），

從小到大排列甲的成績為：2，6，6，7，7，7，8，9，9，9，中位數為7環.

甲成績的方差為：

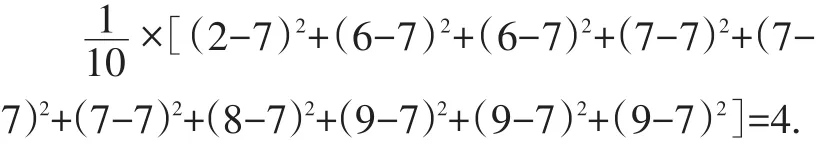
乙的射擊成績為：2，4，6，8，7，7，8，9，9，10，則平均數為：

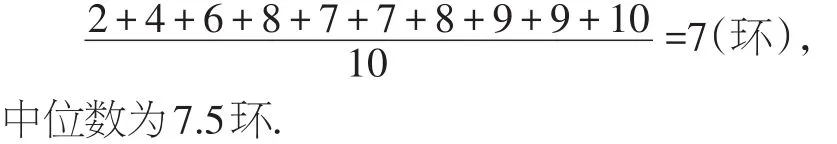
乙成績的方差為：

補全表格和折線圖如下：

甲、乙兩人的射擊成績統計表

（2）甲應勝出.理由：由于甲的方差小于乙的方差，故甲成績較穩定，甲應勝出.

（3）若希望乙勝出，可以制定規則為：命中10環的總次數多的勝出.

理由：因為甲命中10環的次數為0，而乙命中10環的次數為1.

【點評】利用圖表解決數據穩定性的問題注意：

1.從圖表中獲取正確的數據.

2.計算各組數據的平均數、方差.

3.比較大小，確定其穩定性.

三、方差的性質

例3 若一組數據a1，a2，a3的平均數為4，方差為3，那么數據a1+2，a2+2，a3+2的平均數和方差分別是（ ）.

A.4，3 B.6，3 C.3，4 D.6，5

【解析】∵數據a1，a2，a3的平均數為4，

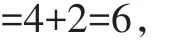
∴數據a1+2，a2+2，a3+2的平均數是6.

∵數據a1，a2，a3的方差為3，

故選：B.

【點評】一組數據x1，x2，x3，…，xn的平均數、方差之間的關系如下：

一組數據方差s2 s2表示形式平均數x x+a x1，x2，x3，…，xn（x1+a），（x2+a），（x3+a），…，（xn+a）kx1，kx2，kx3，…，kxn（kx1+a），（kx2+a），（kx3+a），…，（kxn+a）kx k2s2 kx+a k2s2