無線傳感器網絡立體定位算法與仿真

張留朝，張 彭，劉貞德

（濰坊學院 計算機工程學院，山東 濰坊 261061）

0 引 言

在無線傳感器網絡中，位置信息對傳感器網絡的監測活動至關重要，事件發生的位置或獲取信息的節點位置是傳感器節點監測信息中的重要組成部分，沒有位置信息的監測消息是無意義的[1]。因此，無線傳感器網絡節點定位是其最基本的功能之一，對無線傳感器網絡應用的有效性起關鍵作用。

無線傳感器定位算法包括基于測距的定位和無需測距的定位兩種[2-3]。基于測距的定位算法是利用接收信號強度指示（RSSI）估計待定位節點到參考節點的距離，然后根據測距定位算法計算待定位節點的坐標。典型的測距定位算法包括多邊定位、邊界盒定位、MDS-MAP等[4]。無需測距的定位利用網絡連通性、節點分布、跳數等方法實現定位，典型的無需測距的定位算法包括質心定位、DV-HOP定位和APIT定位等[5-6]。

上述定位算法中，無論是基于測距的定位，還是無需測距的定位都存在以下兩方面的局限：

（1）信標節點的位置無法移動；

（2）待定位節點和信標節點[6]必須在同一平面上，否則定位精度會受影響。

針對上述局限，本文提出了無線傳感器網絡的立體定位方法。

1 立體定位算法描述

本文提出了一種無線傳感器網絡的立體定位算法，設立多個信標節點和一個終端用戶節點，所設立的信標節點不在同一平面上，而是位于“棱錐”或“棱柱”的頂點。建立三維直角坐標系，標定信標節點在直角坐標系中的位置坐標。信標節點在三維直角坐標系中的相對位置和坐標始終不變（信標節點發生移動時，直角坐標系隨參考節點的移動而移動，這樣信標節點在直角坐標系中的位置坐標即可保持）。信標節點負責接收待定位節點發射的無線信號，并根據RSSI測距公式計算出待定位節點到該信標節點的距離。然后把計算得到的這一距離和該待定位節點的身份標識發送至終端用戶節點。終端用戶節點根據接收到的信息計算出待定位節點的位置坐標。

1.1 信標節點分布模型

本文提出的無線傳感器網絡立體定位算法的信標節點不在同一平面上，分別位于“棱錐”或“棱柱”的頂點。建立三種信標節點分布模型，即“三棱錐”分布模型、“三棱柱”分布模型和“四棱柱”分布模型，分別如圖1～圖3所示。

圖1 信標節點“三棱錐”分布模型

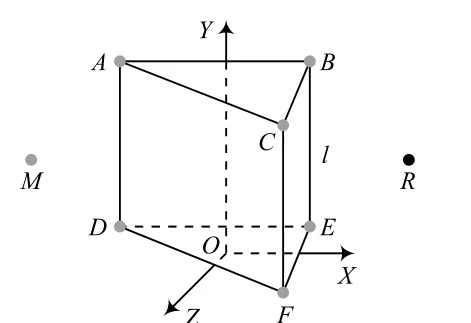
圖2 信標節點“三棱柱”分布模型

圖3 信標節點“四棱柱”分布模型

在上述三圖中，A，B，C，D，E，F，G，H均為信標節點，M是任一待定位節點，R是終端用戶節點。待定位節點M周期性地發送包含自身信息的無線信號至信標節點，信標節點接收待定位節點發送的無線信號后，解析出該節點的身份標識，并測定接收到的信號強度指示RSSI，根據RSSI測距公式[8]計算出待定位節點到此信標節點的距離，然后把這一距離和待定位節點的身份標識發送至終端用戶節點R。終端用戶節點R根據信標節點發送的距離信息計算出待定位節點的坐標。

1.2 立體定位算法

建立三維直角坐標系，標定信標節點在直角坐標系中的位 置 坐 標 A（x1，y1，z1），B（x2，y2，z2），C（x3，y3，z3），D（x4，y4，z4），E（x5，y5，z5），F（x6，y6，z6），G（x7，y7，z7），H（x8，y8，z8），假設待定位節點M的坐標為（x，y，z）。用di（i=1，2，…，8）表示待定位節點到信標節點的距離。具體研究中，通常使用的RSSI定位模型如下[8-10]：

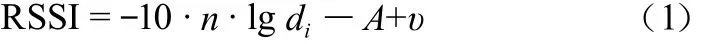
式中：A為信號距離為1 m時，接收信號的功率（dBm）；n為信號傳輸常數，與信號的傳輸環境有關；di為發射節點到信標節點的距離；υ服從（0，δ2）高斯分布，為零均值的隨機測量噪聲，表示環境對數學模型影響的程度。文獻[4]中提到，通過實驗證明，v對距離的計算結果影響不大，因此本文去除υ，用簡化后的信號傳輸模型來估計距離。

用（xi1，yi1，zi1），（xi2，yi2，zi2），（xi3，yi3，zi3） 和（xi4，yi4，zi4）表示圖1～圖3三個信標節點分布模型中任意一組不在同一平面上的四個信標節點坐標，di1，di2，di3和di4分別表示待定位節點到此四個信標節點的距離，則任一待定位節點坐標（x，y，z）滿足如下關系：

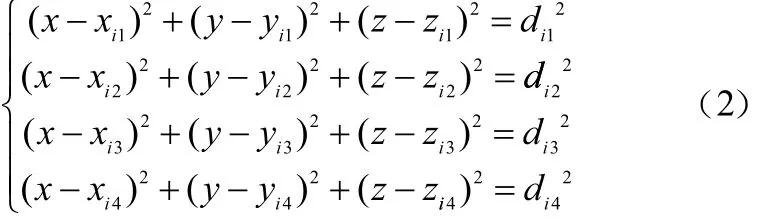
用式（2）中的第1～3個方程減去第4個方程，并表示成線性方程的形式AX=b，其中：

在AX=b兩邊同乘A－1得到X=A－1b，即待定位節點坐標為（x，y，z）。

需要注意的是，在圖1所示的信標節點分布模型中，一共有四個信標節點，只可得一個如式（2）所示的方程組，所以只能計算得到一個待定位節點的坐標。而在圖2和圖3所示的信標節點分布模型中，信標節點的數量分別為6個和8個，可得到多個如式（2）所示的方程組，可由此計算得到多個待定位節點的坐標。在實際應用時，可根據需要取其均值，作為待定位節點的坐標。

2 實驗設計

2.1 實驗環境

信號RSSI在不同環境下對應的距離曲線不同，因此我們搭建了如下實驗環境來進行距離曲線實驗。

上述無線傳感器網絡節點選用網蜂科技有限公司生產的ZigBee模塊，實物如圖4所示，其核心芯片為CC2530。

測試場地選在物聯網實訓實驗室，如圖5所示。

圖4 實驗節點

圖5 測試場地

2.2 實驗方法和結果

實驗時，發送節點和接收節點離地高度均為0.5 m，并保持天線垂直于地面，發送節點和接收節點為直視鏈路，且每隔0.5 m測量接收到的RSSI值。在發送節點和接收節點距離為1 m時，實驗測得的接收信號功率A=41 dBm。通過兩組信號強度-距離測試數據，利用（1）式計算得到n=2.3。把所有的測試數據進行4次Matlab曲線擬合，得到信號強度對應的距離曲線如圖6所示。

3 定位仿真

3.1 信標節點間距對定位精度的影響

本節利用圖1所示的“三棱錐”分布模型探索在室內環境中，信標節點間距對定位精度的影響。定位精度用平均定位誤差表示[11-12]，平均定位誤差的定義如下：

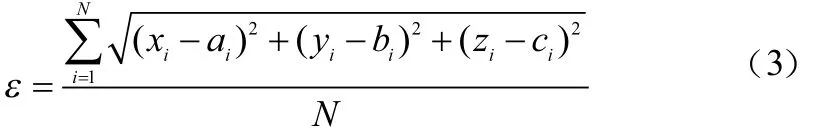
式中 ：（xi，yi，zi）是計算得到的待定位節點的坐標 ；（ai，bi，ci）為實際坐標；N為測試次數。

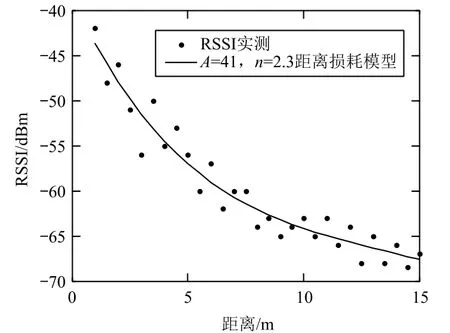
圖6 信號強度對應的距離曲線

仿真步驟如下：

（1）設定圖1“三棱錐”模型中信標節點的間距l，計算每個信標節點在坐標系中的坐標，4個信標節點的坐標分別為

（2）當移動節點處于不同位置時，位置坐標用（ai，bi，ci）表示，分別計算移動節點到4個信標節點A，B，C，D的距離：

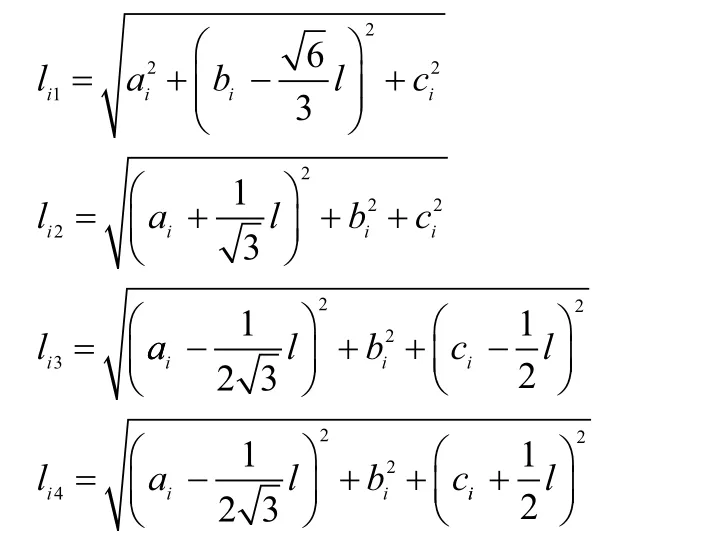
（3）根據步驟（2）得到的移動節點到信標節點的距離，在圖6所示的距離損耗模型中標定對應的信號強度RSSI；

（4）根據步驟（3）標定的RSSI，利用公式（1）計算移動節點到每一個信標節點的距離di；

（5）根據步驟（4）得到的移動節點到每一個信標節點的距離 di，利用公式（2）計算移動節點的坐標（xi，yi，zi）；

（6）將步驟（5）計算得到的移動節點坐標（xi，yi，zi）和移動節點的實際坐標（ai，bi，ci）代入公式（3），計算得到平均定位誤差。

按照上述步驟，利用Matlab2014進行仿真，仿真結果如圖7所示。

從圖7的仿真結果可以看出，平均定位誤差隨著信標節點間距的增加而減小。當信標節點間距為1 m時，平均定位誤差為1.8 m；當信標節點間距為5.5 m時，平均定位誤差為1.38 m。當采用“三棱錐”分布模型，信標節點間距為5.5 m時，比信標節點間距為1 m時的平均定位誤差減小了0.42 m。

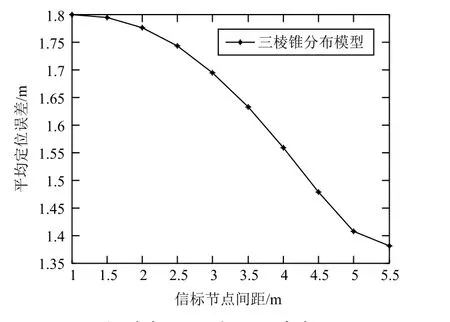
圖7 信標節點間距對定位精度的影響

3.2 信標節點分布模型對定位精度的影響

按照和“三棱錐”分布模型相類似的仿真步驟，當信標節點按“三棱柱”模型和“四棱柱”模型分布時，分別對定位精度進行仿真。

需要注意的是，“三棱柱”模型和“四棱柱”模型中，信標節點的數量分別為6個和8個，可得到多個如式（2）所示的方程組，由此得到多個待定位節點的坐標。所以，在利用（3）式計算時，可得到多個平均定位誤差值。把這多個值取算術平均，得到圖8所示的仿真結果。

圖8 信標節點分布模型對定位精度的影響

從圖8所示的仿真結果可以看出，當信標節點的分布模型為“三棱柱”模型和“四棱柱”模型時，定位精度會隨信標節點間距的增加而提高。當信標節點間距為4.5 m時，“三棱柱”模型和“四棱柱”模型的平均定位誤差最小，分別為1.3 m和1.17 m。從信標節點的三種分布模型來看，“四棱柱”模型性能最優，“三棱柱”模型次之，“三棱錐”模型最差。當信標節點間距一定時，“四棱柱”模型的定位精度比“三棱柱”模型的定位精度高約10%，而“三棱柱”模型的定位精度又比“三棱錐”模型的定位精度高約10%。之所以得到這樣的結果，是因為“三棱柱”模型中信標節點的數量是6個，“四棱柱”模型中信標節點的數量是8個，兩者分別比“三棱錐”模型多出了2個和4個信標節點。所以，定位精度的提高是以多付出的信標節點設備為代價的，這與常見的無線傳感器網絡定位理論相一致。

此外，可由圖8所示的仿真定位誤差曲線看出，采用“三棱柱”模型和“四棱柱”模型，且當信標節點間距大于4.5 m時，平均定位誤差反而會隨著信標節點間距的增大而增大。所以，通過本文的仿真可知，定位精度并非完全隨著信標節點間距的增加而提高。在實際應用中，選取合適的信標節點間距十分必要。

可采用“三棱柱”模型和“四棱柱”模型，當信標節點間距大于4.5 m時，為了減小平均定位誤差，對算法進行優化：“三棱柱”模型和“四棱柱”模型中，信標節點的數量分別為6個和8個，計算時，會有多個如式（2）的方程組，由此計算得到多個待定位節點的坐標。在利用（3）式計算時，可得到多個平均定位誤差值。一旦某個平均定位誤差高于某值，就會舍棄這一組數據。經過優化后的仿真結果如圖9所示。

經優化后，“三棱柱”模型和“四棱柱”模型的平均定位誤差最小值分別為1.15 m和1.05 m，比優化前分別小了0.15 m和0.12 m。

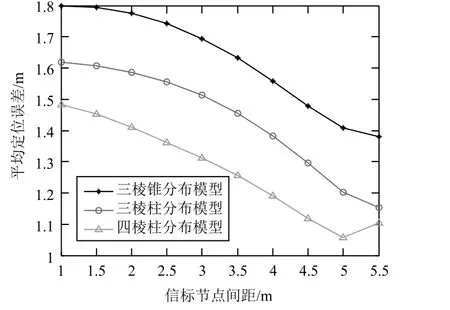
圖9 優化后的仿真結果

4 結 語

本文提出了信標節點可移動的無線傳感器網絡立體定位算法。建立了三種信標節點的分布模型——“正三棱錐”分布模型、“正三棱柱”分布模型和“正四棱柱”分布模型，仿真了不同信標間距對定位精度的影響，以及信標節點分布模型對定位精度的影響。仿真結果表明，本文提出的立體定位算法能準確定位待定位節點的相對位置坐標。本算法將在室內定位、物品追蹤等領域有較廣闊的應用前景。