巖石薄片顯微圖像采集自動聚焦方法

陳旺，滕奇志，何海波，蘇桂芬

（1.四川大學電子信息學院圖像信息研究所，成都610065；2.成都西圖科技有限公司，成都 610065；3.國土資源實物地質資料中心，三河 065201）

0 引言

巖石薄片是地質勘探中獲得的寶貴實物資料，通過光學顯微鏡對巖石薄片進行礦物鑒定是石油地質行業的常規手段，而顯微成像為薄片的數字化保存、信息共享以及圖像處理分析提供了條件。

在顯微鏡下進行薄片圖像采集，一次只能得到一個小視域的圖像，要得到完整的全薄片圖像，需要通過載物臺移動，逐視場采集并將圖像拼接起來。在切換視場的過程中，由于巖石薄片無法達到絕對的平整，因此要求在切換視場后，通過調整載物臺的高度對物距進行調整，保證采集圖像清晰。

在當前的聚焦系統中，分為主動式聚焦和被動式聚焦兩種[1]。主動式聚焦不僅硬件繁雜，而且很容易出現因焦距測量不準確導致聚焦失敗。目前主流采用的聚焦方式為被動式聚焦，該方式通過分析相機實時捕獲的畫面清晰度，對圖像質量做出評價，通過移動載物臺，使之呈現出清晰畫面示意到達焦點[2]。

1 聚焦算法設計

相機捕捉畫面形式為圖像，其模糊狀態下和清晰狀態下所含納的信息量具有顯著差異，在描述圖像信息含量時，通常采用圖像梯度的方式，圖像梯度表示當前像素與相鄰像素的差異情況，梯度越大，圖像表現為邊緣更明顯，包含信息量更大；梯度越小，表示該像素處于圖像的平滑區域，包含信息量越少[3]。因此，可以根據圖像的梯度信息含量作為圖像聚焦狀態的參考值。通過調整載物臺的高度使之達到清晰度最高的點，達到聚焦的目的。

1.1 清晰度評價函數

聚焦準確的前提是所選擇的清晰度評價函數能夠判斷當前圖像清晰與否，優秀的清晰度評價函數，其曲線應具備單峰、陡峭、準確、平滑等特性[4-5]。清晰度評價函數的工作通俗意義上就是將視覺上圖像的感官清晰與否以數值高低的形式表現出來。以下為常用的清晰度分析方法[6]。

（1）時域分析法。時域分析法主要是獲取原始圖像的梯度信息，根據梯度數值大小示意細節豐富程度。常用的時域分析法主要有Sobel函數、灰度差分絕對值之和函數法、Robert函數法、灰度方差函數法等。

（2）頻域分析法。頻域分析法原理是將圖像進行傅里葉變換或小波變換，依據其能量分布，設置下限頻率，通過累計高頻能量值的多少，從而判斷清晰度。

（3）信息熵分析法。信息熵分析法是基于香農理論，通過對原始圖像進行信息熵的計算，判斷圖像清晰度，通常信息熵越大，圖像越清晰。

通常，時域分析法較頻域分析法、信息熵分析法更具優勢。小波變換和傅里葉變換等頻域分析法計算量大，空間梯度通過相鄰像素灰度值的簡單計算即可獲得，而熵函數靈敏度較低，根據圖像內容差異可能出現與實際情況相反的結果。

本文采用Sobel函數作為清晰度評價函數，該函數采用Sobel算子對原始圖像水平和垂直方向進行邊緣信息量提取，并累計梯度信息，計算出清晰度值。

假設采用內核為3的Sobel算子提取圖像梯度分量：

（1）橫向梯度：

式中，F(x,y)為待進行邊緣提取的圖像，Gx(x,y)為與橫向Sobel算子卷積后的臨時結果圖像。

（2）縱向梯度：

式中，F(x,y)為待進行邊緣提取的圖像，Gy(x,y)為與橫向Sobel算子卷積后的臨時結果圖像。

（3）近似梯度：

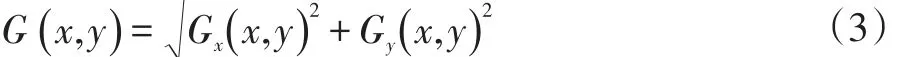
式中，Gx(x,y)，Gy(x,y)為待進行邊緣提取的圖像，G(x,y)為綜合橫向、縱向邊緣梯度提取后的結果圖像。

（4）清晰度評價函數：

式中，D為清晰度計算結果，M為圖像寬度，N為圖像高度，G(x,y)為綜合橫向、縱向邊緣梯度提取后的結果圖像。

1.2 聚焦區域與爬山對焦

在聚焦過程中，需選取一定的區域作為清晰值計算的來源。區別于全景聚焦，選取部分區域作為清晰度計算區域可以大大降低計算量，有效提高清晰度值的計算效率[2]。

聚焦區域選取目前主要采用1D區域選擇、中心取窗區域選擇、多點取窗區域選擇、非均勻采樣等主流算法[7]，對于顆粒信息豐富的巖石薄片，采用以上方法均能取得良好效果，但是，在實際應用中存在大量目標稀疏的薄片，而選取固定位置進行單點聚焦往往無法包含顆粒信息而造成誤判，導致聚焦不準確甚至聚焦失敗。

針對以上問題，本文采取多點聚焦的方法，單獨對每一區域進行清晰度值計算，選擇清晰度值最大的兩個位置，其結果求和作為最終清晰度值。空白區域不含目標顆粒，而光線波動加重了清晰度評價函數曲線的毛刺現象，經大量實驗分析，同一薄片，其空白區的清晰值不高于該薄片目標顆粒區清晰值的1/3，利用這種特性，可判斷出該位置是否空白，從而在聚焦過程中有效規避空白區域。

如圖1所示，本文選擇四個位置進行多點聚焦，若四個位置計算后清晰度值依次為D1，D2，D3，D4且D1>D2>D3>D4。根據本文算法，最終清晰度值為V=D1+D2。

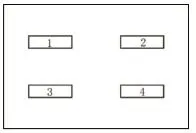
圖1 聚焦位置

聚焦算法中，最主要的三個部分為：聚焦區域選擇、清晰度評價函數設計、峰值點搜索策略[8]。選擇聚焦區域與清晰度評價函數后，合理設計搜索策略尤為重要。

傳統的搜索策略采用固定步長爬坡聚焦，首先試探性垂直移動載物臺固定距離，再根據移動前后清晰度值對比，可判斷出正確的搜索方向，再使用爬坡法搜索焦點。

具體算法如下：

（1）計算當前位置清晰值V1，載物臺試探性向下移動固定步長，計算移動載物臺后視場的清晰值V2；

（2）比較載物臺移動前后的清晰度值，若清晰度值增大，則按原方向移動載物臺固定步長，若清晰度值減小，則按原方向的反方向移動載物臺固定步長；

（3）重復步驟2，直至載物臺移動出現反轉。

在薄片的制造過程中，受限于制作工藝，薄片往往存在局部不平整的情況，通常，在切換視場后需重新搜索新市場的焦點，如下圖2所示，受光線波動的影響，清晰度評價函數曲線存在大量毛刺，該毛刺的存在可能導致聚焦不準確甚至聚焦失敗，尤其是切換視場后，當前位置偏離新市場焦點較遠時，清晰度評價函數曲線在該點附近較為平緩，毛刺影響顯著，移動的步長過小使得聚焦陷入局部極值，導致聚焦失敗；而在焦點附近，移動步長過大使得聚焦不準確，偏離焦點較遠甚至成像模糊聚焦失敗。因此在實際設計搜索算法時，不能采取固定單一步長進行聚焦，聚焦步長需根據當前偏離焦點的多少具有可變性：離焦點較遠時，采用大步長進行聚焦；離焦點較近時，采用小步長進行聚焦[9-10]。

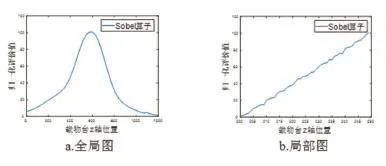
圖2 清晰度評價函數曲線

觀察清晰度評價函數曲線上升（下降）段，曲線呈現出明顯拐點，該拐點可反映出曲線斜率的增減。對于實際聚焦過程，測繪完整的清晰度評價曲線尋找拐點準確位置不僅耗時，而且繁瑣。數學上拐點的定義給予我們靈感，當曲線從“凹增”變化為“凸增”時，其割線斜率從增大變化為減小。計算割線斜率只需記錄聚焦過程載物臺移動前后其清晰度值及移動步長。通過判斷割線斜率的增長（減小）趨勢，能夠大致得到拐點范圍，從而選擇合適的步長進行聚焦。

以曲線上升段為例，拐點以左，斜率增大；拐點以右，斜率減小。在斜率增大的區間段，此時偏離焦點較遠，宜采用大步長進行焦點的搜索；在斜率減小的區間段，此時已接近于焦點，宜采用小步長進行精確搜索。

具體算法如下：

（1）計算當前位置清晰值V1,載物臺試探性向下移動固定步長，計算移動載物臺后視場的清晰值V2；

（2）比較載物臺移動前后清晰度值V1、V2：

若V1>V2,則往上移動載物臺同等固定步長，并記錄移動后的清晰度值V3,若|V3-V1|>|V2-V1|,采用大步長進行聚焦，反之，采用小步長進行聚焦；

若V1＜V2，則往上移動載物臺同等固定步長，并記錄移動后的清晰度值V3,若|V3-V2|>|V2-V1|,采用大步長進行聚焦，反之，采用小步長進行聚焦。

（3）按傳統爬坡法進行焦點搜索，當清晰度值增減由急升變為平緩時，改用小步長。

2 實驗結果分析

為了體現本文算法的優勢，選取巖石顆粒較為稀疏的視場進行聚焦。實驗采用偏光顯微鏡，載物臺垂直方向電機精度0.001㎜，設置單次步長0.01㎜。相機分辨率3456×2304，程序基于VS2010平臺開發實現，假設視場長度為W，高度為H。

本文算法選取計算范圍如下：

位置1起點（2*W/15,H/4）

位置1終點（11*W/30,7*H/20）

位置2起點（19*W/30,H/4）

位置2終點（13*W/15,7*H/20）

位置3起點（2*W/15,13*H/20）

位置3終點（11*W/30,3*H/4）

位置4起點（19*W/30,13*H/20）

位置4終點（13*W/15,3*H/4）

計算面積占視場面積7/75,聚焦面積占視場面積7/150。

采用不同的清晰度評價函數，其邊緣檢測效果不同，本文對比拉普拉斯函數、Sobel函數、雙線性濾波Sobel函數法、灰度方差函數法、Robert函數法，定向移動載物臺，使用多種算子計算圖像清晰度，繪制清晰度評價函數曲線如圖3。

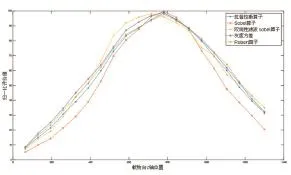
圖3 不同算子清晰度評價函數曲線

從圖像上看，基于拉普拉斯算子、Sobel算子、灰度方差、Robert算子的清晰度評價函數均具有良好的無偏性，經雙線性濾波后的Sobel函數其峰值偏離焦點較遠，以上清晰度評價函數均滿足單峰性要求，相比于其他清晰度評價函數，基于Sobel算子的清晰度評價函數更為靈敏且存在明顯的拐點，適宜于本文搜索策略，能夠達到快速聚焦的目的。

3 結語

本文所提出的基于Sobel算子多點聚焦算法雖然存在波峰較寬的不足，但具有良好的無偏性、單峰性、快速性，特別是在目標顆粒不均勻的情況下，比傳統的聚焦算法具有更加優秀的抗噪性能。結合基于斜率變化的變步長搜索策略，本文的自動搜索算法可以實現巖石薄片顯微圖像采集的自動聚焦。