中國省際碳排放額度分配方法研究

李小勝 李 月 李 燕

(1.安徽財經大學 統計與應用數學學院,安徽 蚌埠 233030; 2.吉林大學 商學院，吉林 長春 130012)

一、引言及相關文獻回顧

2009年《聯合國氣候變化框架公約》第15次締約方大會在哥本哈根召開前夕，中國政府鄭重承諾到2020年單位GDP碳排放強度在2005年的基礎上降低40%～50%。由于中國各省份的經濟發展水平和技術水平存在著顯著差異，未來各個省份的減排潛力也會不同。為了落實降低碳排放強度的承諾，根據效率和公平的原則，需要在碳排放總額固定的情況下，重新分配各個省份的碳排放額度，減少排放效率低的省份排放額度，增加排放效率高的省份額度，這也有賴于各個地區的合作。現實中碳排放額度的分配存在著很多方法，各有優勢和劣勢。但現有的方法多是從一個指標或者幾個指標的簡單線性加權組合得出碳排放分配額度，因而有可能考慮的因素不夠全面。本文利用改進的數據包絡模型，即“零和博弈”數據包絡(Zero Sum Gains DEA，ZSG-DEA)模型，既考慮多投入和多產出，又考慮在效率提升情況下的重新分配，對中國30個省份的二氧化碳排放總額進行重新分配，較以往的單指標研究，這種分配考慮的指標更全面，結果更加合理。

在現有文獻中，學者們采用不同的方法研究了碳排放額度分配問題。Gomes et al.(2008)首先利用“零和博弈”數據包絡模型，將二氧化碳排放作為唯一投入變量，人口、GDP和能源消耗作為產出變量對《京都議定書》簽約國家中的64個國家的CO2排放進行重新分配，分配后所有國家的效率都為1。Wu et al.(2013)采用全局效率最大化的博弈模型對歐盟15個成員國的農業溫室氣體排放的效率進行估計，并對排放額度進行重新分配，分配后的總效率達到最大化。Wu et al.(2014)采用考慮期望產出和非期望產出都同時擴張的數據包絡(DEA)模型對中國各省份2007—2011年的工業效率進行評價，并計算了各個省份期望產出增加的數量和非期望產出應該減少的數量。Wang et al.(2013)采用考慮了松弛作用的“零和博弈”效率評價模型，對2020年中國各個省份CO2排放額度、能源消耗和非化石能源消費等三種投入進行了重新分配。林坦等(2011)根據Gomes et al.(2008)思想對2009年歐盟21個成員國的碳排放額度進行了重新分配。

本文認為，根據“零和博弈”思想，首先，Gomes et al.(2008)將CO2排放看成是唯一的投入，將人口、能源消耗和GDP作為模型產出變量，對歐盟各國碳排放額度進行重新分配。這種對數據的投入和產出的處理方式明顯不符合經濟學原理。目前比較公認的是將CO2排放看成是非期望產出， GDP作為產出指標，就業人員或者人口數、能源作為投入指標。其次，林坦等(2011)對Gomes et al.(2008)的模型進行改進，考慮了多個投入，其中一個投入按照“零和博弈”進行競爭，但模型只針對存在競爭的投入減少比例進行優化而忽略了其他投入，這種情形與大多數的實際生產活動不相符合。最后，苗壯等(2012)考慮了非期望產出的弱可處置性，在規劃模型中采用等式的形式進行約束，并采用產出競爭的形式來研究CO2排放額度分配，但是效率的測算卻限制在對CO2排放額的改進中，并未考慮期望產出GDP，因而模型對應的生產可能集并不符合弱可處置生產可能集特征。鑒于上述研究的不全面，本文利用“零和博弈”DEA模型對相關問題做進一步探索，并對中國2012年碳排放額度進行重新分配，擬為后續的中國碳排放交易市場額度分配提供依據。

二、“零和博弈”DEA方法

(一)“零和博弈”DEA模型

在采用數據包絡分析模型對決策單元(DMU)的效率進行評價時，各決策單元投入和產出之間互相獨立。實踐中經常會出現所有決策單元的總產出或者總投入是固定的情況下，一個個體增加投入或者產出，另一個個體必然發生減少投入和產出的情況，Lins et al.(2003)將這種研究資源競爭情況下的博弈模型，叫做“零和博弈”數據包絡分析(ZSG-DEA)模型。他們在其研究中針對這種資源間的競爭關系，考慮了兩種情況：一種情況是一個決策單元增加的數量，正好是其它決策單元減少這個數量的平均分配。例如分別有A、B、C三個決策單元，它們的產出分別是20、40、60。決策單元A想提高產出8個單位，即產出為28，按照其他決策單元減少相同數量的原則，那么B減少4個單位，變成36個單位，C減少4個單位，變成56個單位，這種分配原則是總的產出不變，某個單元的增加量正好等于其他單元減少量的和，并且是在其他個體間進行平均分配。另一種情況是按照比例分配，即依據決策單元產出大小進行比例分配，即A單元的產出為28時，增加的8個單位在B、C單元間按照產出的比重進行分配，即B減少8×40/(40+60)=3.2，變為36.8，C減少8×60/(40+60)=4.8，變為55.2，三者的總量還是不變，這種分配方式考慮各自的產出大小，明顯較上述的平均分配合理。

Gomes et al.(2008)認為，在投入導向下按照比例分配的原則，一個決策單元無效的話，它必須通過減少投入變成有效，而減少的投入按照比例分別增加到其他單元的投入上，設有n個決策單元(DMUj)(j=1,…,n)，每個決策單元有相同的m項投入xij(i=1,…,m)，s項有競爭關系的產出yrj(r=1,…,s)，q項無競爭關系的產出 zpj(p=1,…,q)，λj表示決策單元權重，具體的決策單元用j0表示，對于投入之間存在著競爭關系的ZSG-DEA模型，可以用下式來表示：

(1)

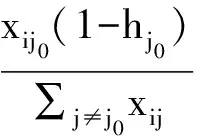
對于產出之間存在著競爭關系的ZSG-DEA模型，可以用下式來表示：

(2)

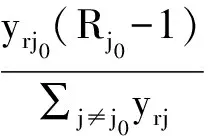
式(1)和式(2)為非線性規劃，Lins et al.(2003)已經證明ZSG-DEA模型在單個投入具有競爭關系時，與經典的數據包絡模型之間存在著轉換關系。令決策單元經典的效率評價值分別為θk、θj等，W是效率值小于1的決策單元的組合，定義qkj=θk/θj， “零和博弈”模型的效率值hk與經典的效率值之間存在下列關系：

(3)

當產出之間存在競爭性關系的ZSG-DEA的效率值為Rk時。令個體經典的效率評價值分別為Vk、Vj，定義Qkj=Vk/Vj，那么Rk與經典的DEA效率之間的關系，可以表示為：

(4)

通過上述變換，我們發現單個投入或者產出存在著競爭關系的非線性模型，可以很方便地從經典的投入產出模型中推導出競爭性資源情況下的效率值。但是式(3)和式(4)應用的條件是只有一個投入或者產出之間存在著競爭關系才能成立。首先，Wu et al.(2013)認為這種模型太理想化，不太現實，在他們的研究中提出了全局的效率最大化。其次，模型的應用條件是只有一個產出和投入具有“零和博弈”關系時才能成立，一種投入的減少或者一種產出的增加，并不容許其他投入和產出同比例的縮減和擴張，這種設置明顯不符合數據包絡的原理，只是在Lins et al.(2003)和Gomes et al.(2008)的文章中才成立，因為他們只研究了一種投入，并且是具有競爭性關系的投入。Wu et al.(2014)的模型不但研究了具有競爭性關系的投入和產出，還考慮了沒有競爭性關系的投入和產出，所以這種模型更加適合現實情況。目前國內外的其他文獻并沒做如此設置，為了符合Wu et al.(2014)的設定，我們對模型進行修改，在具有競爭性關系的產出或投入的分配基礎上也考慮了非競爭性產出或投入的擴張(或減少)。

(二)改進的“零和博弈”DEA方法

采用數據包絡模型對CO2排放績效和額度分配進行研究，涉及CO2排放數據究竟是投入還是產出，目前國際上還存在爭議：一是將其看成是弱可處置性，在模型中用等式表示。二是將CO2排放看成產出，但要進行數據處理，要么取倒數，要么所有數據取負號，再進行平移變化，這種方法在Seiford et al.(2002)研究中有所體現。三是將CO2排放看成投入，這種方法符合生產中投入要素的基本原理，即投入越少越好。目前對于環境績效進行評價的模型，應用最多的方法是將CO2看成弱可處置或者看成產出。在研究資源的競爭性模型時幾乎都是采用最后一種方法，即把CO2排放看成投入，是越小越好的變量，Gomes et al.(2008)、林坦等(2011)、鄭立群(2012)、Wu et al.(2014)、Wang et al.(2013)都采用這種方法。若看成是弱可處置性，則不適合研究競爭性模型要求，因為等式約束時，CO2排放數據究竟是按照產出還是按照投入競爭的形式就會存在困難。本文將CO2排放也按照投入處理，根據這種思想和上述的數據來源，本文構建以下公式：

(5)

式(5)中的符號和式(1)以及數據來源中的符號是一致的，其中，∑jλi=1表示規模報酬可變，Lins et al.(2003)認為現實生產的理論沒有證據表明是規模報酬不變的，所以本文也設置為規模報酬可變。從式(5)我們可以看出其與以往的模型明顯不同，即不但能夠處理多個投入具有競爭關系，而且還考慮了沒有競爭關系的個體間的投入按比例縮減情況。根據式(5)，我們采用中國2012年的碳排放等數據對CO2排放的額度進行重新分配，擬為中國碳排放交易市場的初始額度確定提供一些定量基礎。

三、數據來源和實證結果分析

(一)數據來源

根據研究碳排放額度分配模型的要求，我們選擇三項投入指標：(1)各個省區的能源消費(Ei)，數據來自《中國能源統計年鑒》。(2)就業人數(Li)，數據來自各省份統計年鑒和《中國統計年鑒》。(3)資本存量(Ki)，對于期初的資本存量，我們采用Hall et al.(1999)的方法，Ki0=Ii0/(δ+gi)，Ii0表示固定資本形成總額，δ表示折舊率，本文取8%，gi表示各個省份的GDP的平均增長率，以1978年為基期，按照永續盤存法公式Kit=(1-δ)Kit-1+Iit得到各省份資本存量數據，然后調整成2005年不變價。產出指標主要包括：期望產出為地區生產總值，數據來自《中國統計年鑒》，選用2005年不變價GDP表示。非期望產出是CO2排放，參照IPCC的方法和國內外的文獻，我們采用能源消費和碳排放系數之間的關系進行核算，具體可以參照杜立民(2010)等文獻。由于西藏的數據不全，我們只研究了中國大陸30個省份。

(二)實證結果分析

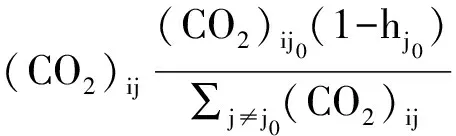
表1 ZSG-DEA模型下各省份CO2排放額度

注：人口數，單位為萬人；各省份GDP是以2005年價表示的，單位為億元；2012年各省份CO2排放，單位為萬噸。

從以上結果我們可以看到，按照效率最大化原則，采用ZSG-DEA模型分配效果較好，模型有一定的合理之處。但是上述結果也有令人不滿意的地方，分別是寧夏和山東，一個是投入和產出都較小的省份，一個是投入和產出都較大的省份，最終的結果是寧夏的效率高于全國的平均值，山東的效率低于全國的平均值，寧夏應該增加碳排放的額度，山東應該減少碳排放的額度，這有可能是由于決策單元的數目不是非常多，從某種程度上導致構造的生產前沿面不能反映一些極端值的情況。但從本文的整體研究看，采用ZSG-DEA模型進行分配后的結果還是比較符合實際情況的，特別是效率的高低與現實的經濟表現密切相關。

我們將依據ZSG-DEA模型進行重新分配后的碳排放數據和其他投入數據代入式(5)中，發現遼寧、吉林、福建的效率值為0.999，其余各個省份的效率值都為1，這種結果表明重新分配后的額度能夠使所有個體的效率達到最大化，是最優的分配，模型不需要按照“零和博弈”的思想繼續分配。

(三)實證結果比較分析

上述的分配是從全要素的角度出發，考慮效率最大化情況下各省份之間CO2的重新分配。從分配的結果看，發達省份基本都是排放較少的狀態，效率低和經濟不發達省份的CO2多數處在超排狀況，這一結果符合目前經濟的發展狀況，也符合效率的原則。除了從投入和產出的角度考慮外，很多學者認為還要考慮公平的原則，例如，國際上關于中美碳排放的數值大小問題的爭論，丁仲禮(2010)認為沒有考慮人均排放和累積排放這兩個指標。陳文穎等(1998)提出碳排放的混合機制，其實是部分考慮了效率的原則。本文結合這兩種思想，提出按照人口和排放強度的角度來進行分配的原則。將該種原則與按照ZSG-DEA效率的原則進行比較分析。設MQTi為第i個省份調整后的排放額度，POPi為第i個省份的總人口，QTi為第i個省份的排放量，QTg為一個國家允許的總排放額度，GDPi為第i個省份的生產總值。依據人口分配的原則得到各個省份的排放，可以用式(6)表示。式(6)是從公平的角度對碳排放額進行測算，認為人均排放應該相等是基本的公平原則。

(6)

按照CO2排放強度的原則進行分配得到各個省份的額度，可以用式(7)表示。式(7)是利用單個指標，從效率的角度對各省份碳排放額進行測算。

(7)

從公平和效率的角度考慮，按照上述兩個原則進行混合分配，得到各個地區的額度，可以用式(8)表示。

(8)

依據各省份人口分配額度的原則，即式(6)，得到重新分配后的額度即表2中的第(3)列。按照排放強度分配額度的原則，即式(7)，得到重新分配后的額度即表2的第(5)列。按照排放強度和人口混合分配的原則，即式(8)，得到重新分配后的額度即表2的第(7)列。依據上述原則，我們分別計算了重新分配后的額度與原來實際的排放之差，從表2中可以看到：按照人口分配額度的原則，額度增加的有16個省份，額度減少的有14個省份。可以發現，很多發達省份重新分配后的額度大于原來的排放，例如上海、江蘇、天津、山東增加了額度。按照排放強度分配額度的原則，額度增加的省份有17個，額度減少的省份有13個。發達省份江蘇、山東減少了額度。按照人口和排放強度進行混合分配，排放額度增加的有19個省份，減少的有11個省份，與按照排放強度進行分配的結果一樣，江蘇、山東與原來的排放相比，額度仍然是減少的。而按照ZSG-DEA模型計算結果來看，發達省份中只有山東出現了額度減少狀況，額度增加和額度減少的省份明顯較后續單個指標計算的結果合理。發達省份重新計算后的額度一般都大于原來的排放數據，即出現額度增加的情況，但是按照上述單指標計算的原則，明顯沒有按照ZSG-DEA模型計算的合理。可見，按照ZSG-DEA模型所確立的碳排放額度可以為未來碳排放市場的初始額度分配提供一定的參考。

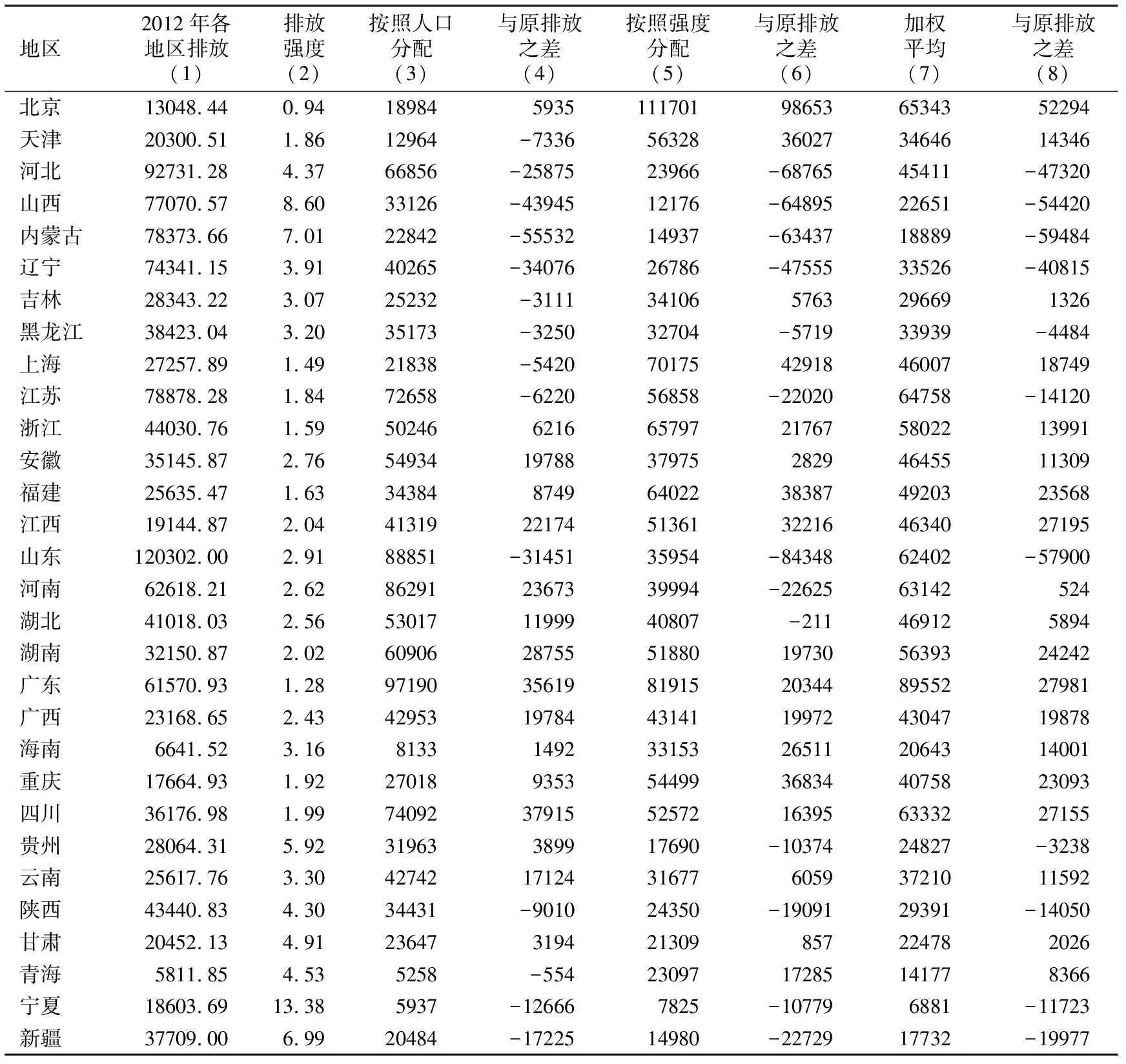
表2 按照公平、效率和兩者混合分配的結果

四、結論及進一步研究方向

碳排放交易市場是適應新常態下經濟可持續發展需求，降低碳排放、發揮市場作用的重要機制設計，但是好的制度設計需要論證不同制度的微觀影響。本文正是在這樣的背景下，應用改進的“零和博弈”DEA(ZSG-DEA)模型對中國碳排放的額度進行分配。研究結果表明，以考慮效率最大化為目標，各省份CO2重新分配后的效率明顯提高。從分配的結果看，發達省份的CO2基本都是排放較少的狀態，效率低和經濟不發達省份的CO2多數處在超排的狀態。由此提醒我們，對于效率低下和碳排放超標的省份，應該轉變經濟發展方式，調整產業結構，否則一旦建立統一的碳排放市場，按照效率分配的原則實施初始額度分配，這些地方的排放額度不足，需要從市場上進行購買，就會加重其經濟負擔，導致其陷入“貧窮的陷阱”。同樣按照效率分配的思想也可以為中國碳排放市場的初始額度確定提供參考依據。

為了論證按照ZSG-DEA效率分配結果的合理性和有效性，本文最后采用考慮公平和效率的單指標進行分配，發現其效果并沒有按照ZSG-DEA模型分配的好，這表明按照ZSG-DEA模型進行分配更加符合經濟的發展狀況，符合國家的整體利益。 從本文的研究來看，按照ZSG-DEA模型分配的思想也出現了一些不盡合理的地方：首先是山東的效率低于寧夏，但是從單個指標排放強度看，山東明顯好于寧夏，這有可能是數據包絡分析模型的樣本容量不足所造成的，極端值導致構造前沿面時不盡合理。其次，有關中國碳排放額度分配的研究，由于數據缺乏，目前都是分析省級額度的分配問題，下一步的研究方向應該是企業間的分配問題，因為參與碳排放交易市場的主體是企業。