一類特殊矩陣的特征值

烏仁其其格

（赤峰學院 數學與統計學院，內蒙古 赤峰 024000）

1 預備知識

定義1.1[1]設A是n階方陣，若存在數λ和n維非零向量x，使關系式Ax=λx成立，則稱數λ是方陣A的特征值，非零向量x稱為A的屬于特征值λ的特征向量.

定義 1.2[1]的特征多項式，它是以為λ未知數的一元n次多項式，也記為 f(λ).稱 |λE-A|=0 為 A 的特征方程.

定理 1.1[1]設 n 階方陣 A 的特征值為 λ1,λ2,λ3,…,λn，則：

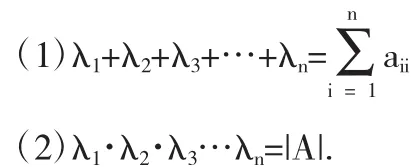
2 主要結論

定理2.1 反對角矩陣

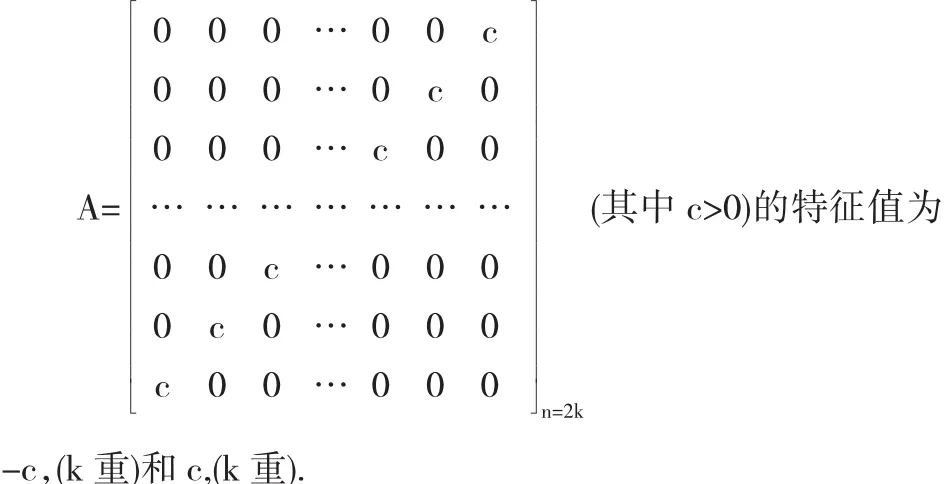
證明 用數學歸納法，

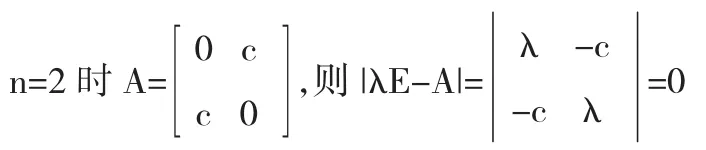
λ2=c2，解得 λ1=c，λ2=-c

假設 n=2k-2，時

得 λ1=c，(k-1 衙） λ2=-c(k-1 重)成立.

得，λ1=c，（k重）λ2=-c,（k重）成立.

定理2.2反對角矩陣

證明用數學歸納法，

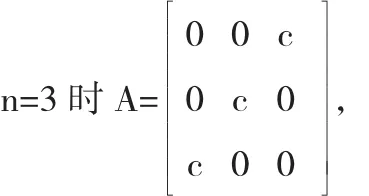
(λ-c)(λ2-c)=0，解得 λ1=c,(2 重) λ2=-c

假設 n=2k-1，時

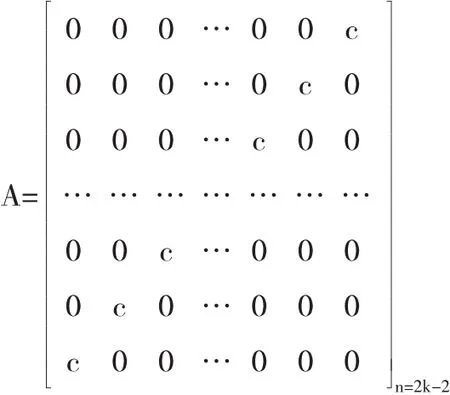
從 |λE-A|=0，得(λ-c)k(λ+c)k-1=0，

得 λ1=c,(k重) λ2=-c(k-1重)成立.

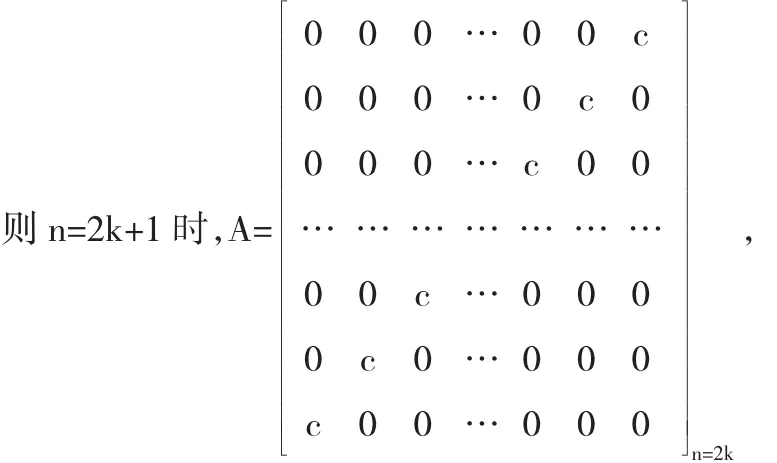
則A的特征方程為|λE-A|=0

A的特征多項式為：

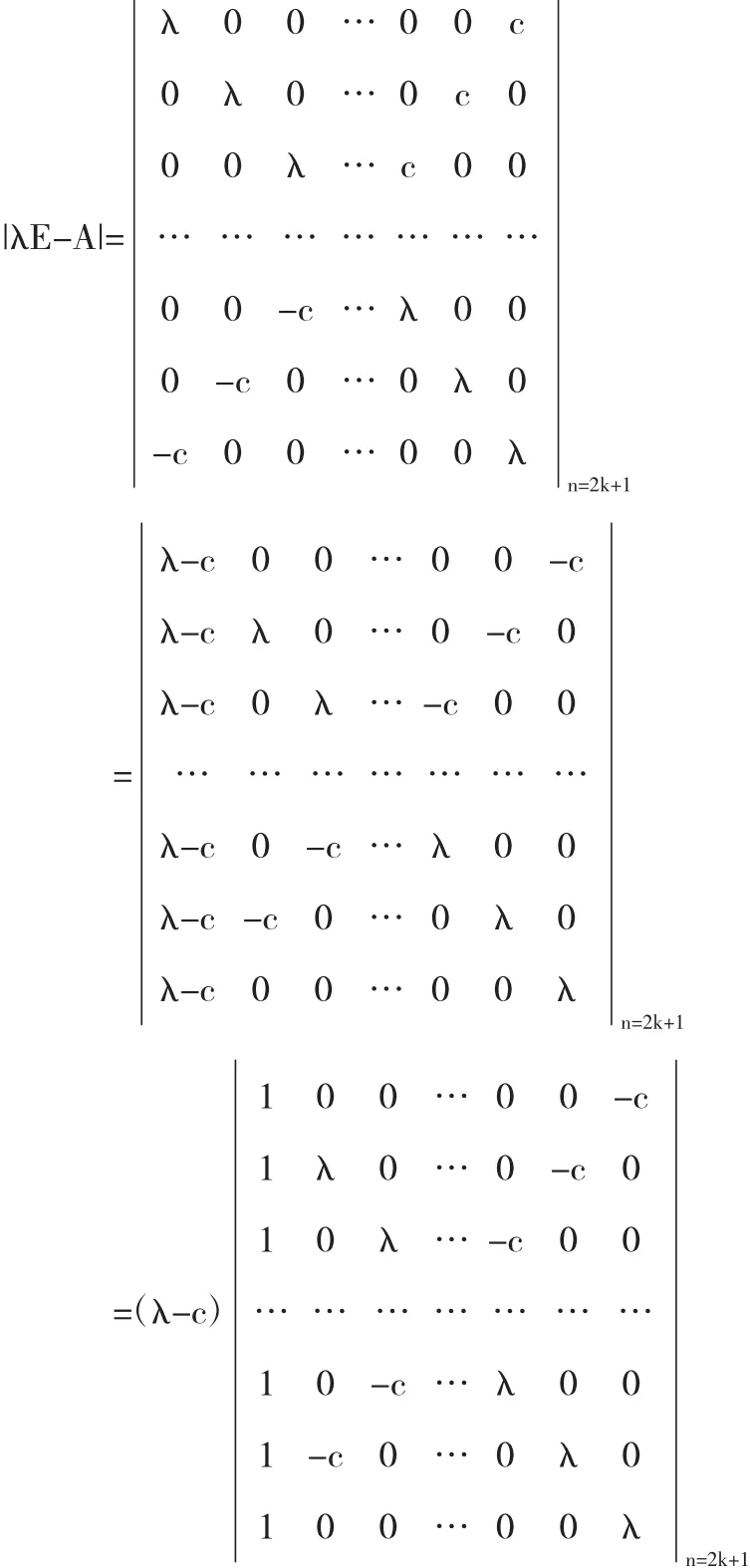
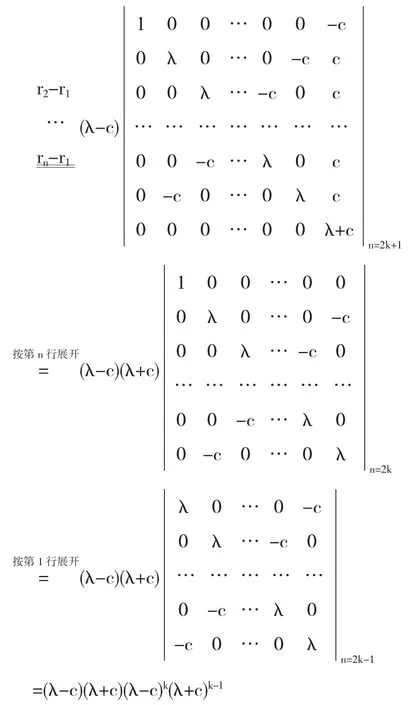
解(λ-c)(λ+c)(λ-c)k(λ+c)k-1=0 得，

得，λ1=c，（k+1重）λ2=-c,（k重）成立.

推論2.1反對角矩陣

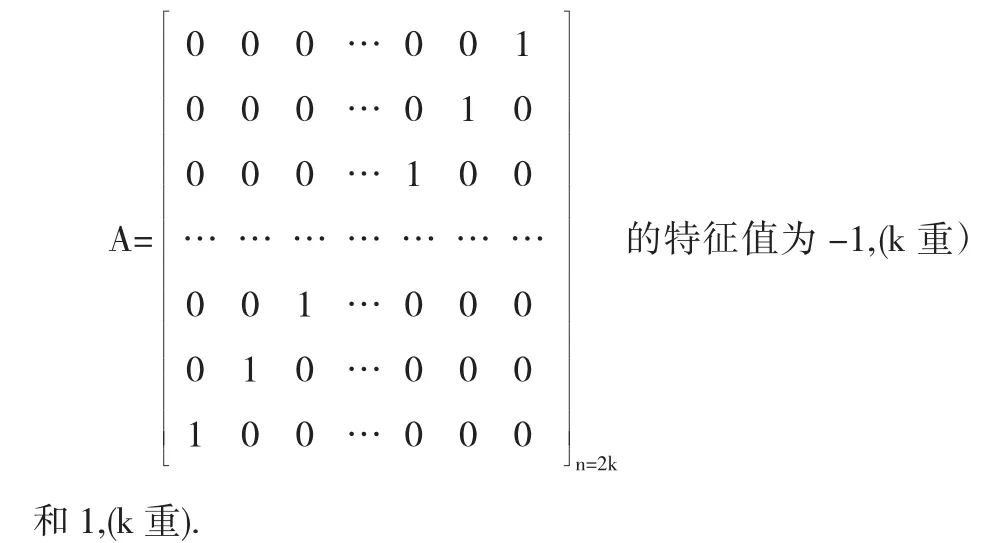
推論2.2反對角矩陣和1(k+1重).

定理2.3設n階方陣

證明由定理1.1[1]和定理2.1可知顯然成立.

定理2.4設n階方陣

證明由定理1.1[1]和定理2.1可知顯然成立.