應用Tsallis算法和關鍵度度量的決策樹構建

李 梁，叢培強，陳亞茹

(重慶理工大學 計算機科學與工程學院， 重慶 400054)

決策樹是機器學習的主要方法之一，在一些領域仍在積極研究，如圖像插值、語音綜合[1-5]。決策樹是根樹結構，容易理解，并且有較好的計算結果和計算效率，其中每個非葉節點是決策節點，其表示將情況分成兩個或多個子樹的標準，每個分支代表當前節點1種分類情況，每個葉節點表示整個數據集1種分類情況，自根節點至每個葉節點存在1條路徑，代表1種分類途徑。決策樹分類器是自上而下的構建過程，并進行預剪枝和后剪枝，預剪枝是在完全正確分裂訓練集之前，較早地停止樹的生成，后剪枝是在完全生成樹結構后進行剪枝。決策樹分類器通過使用節點中的條件來決定分支，從根節點向下移動到葉節點，從而為任何看不見的情況預測類別。

當前有很多文章對決策樹提出了改進，徐鵬等[6]提出C4.5-K，在C4.5中引入了可調節參數K，限制信息增益率的取值范圍，取得較好的性能，但是該算法只面向期貨數據有較好效果；李孝偉等[7]提出了基于分類規則選取的C4.5改進算法，但對復雜樣本分類問題有待進一步研究；宋廣陵等[8]提出了A-CART，能產生多個子節點，但是該算法只適用于兩分類問題。

決策樹的核心問題是樹的構建過程，也就是屬性的分割問題，在過去幾十年出現了一系列文獻，提出了一些分割算法，其中最具代表性的如ID3、C4.5、CART等。ID3基于香農熵構建決策樹；C4.5基于信息增益率，被認為是歸一化的香農熵，彌補了ID3不能處理連續屬性的缺陷；而CART算法基于基尼系數。這些算法是獨立存在的，都有各自相應的優勢。本文提出了一個統一的Tsallis熵框架，這不僅統一了上述3種流行分割標準，而且還可以通過可調參數q值來適應各種數據集。

訓練樣本集存在樣本分類不平衡的情況，也存在小類屬數據集的問題，即在訓練集中有些類屬的樣本數量遠遠小于其他樣本數量，見表1。假設構建的決策樹只有2個葉節點，A1和A2表示當前葉節點樣本數據類別，即A1和A2樣本數據各有 2 000個和200個，A2屬于小類屬；在決策樹構建過程中，對葉節點進行類屬標識時，采用“少數服從多數”的標準，即在對葉節點進行類屬標識時，選出該節點樣本數量最多的類，并以該類標識葉節點。對表1而言，葉節點1與葉節點2均被標識為A1，小類屬A2被忽略。由于上述兩點，使得小類屬被忽略，在預測新數據時，無法判別出小類屬數據。 為解決該問題，本文提出關鍵度度量，取代“少數服從多數”的標準。

表1 訓練樣本實例

1 Tsallis熵框架

1.1 Tsallis熵

為了解決非廣延熵問題，Tsallis受多重分形的啟示，提出了非廣延熵的概念。 Tsallis熵定義如下：

，q∈R

(1)

其中：X取值為{X1，X2,…,Xn}；隨機變量p(Xi)是Xi的概率。

1.2 Tsallis熵框架

香農熵、增益比率和基尼指數統一于Tsallis熵框架中，Tsallis熵與三者的具體對應關系如下：

1) 當可調參數q→1時，Tsallis熵等價為香農熵。

(2)

2) 當可調參數q→2時，Tsallis熵等價為基尼指數Gini。

(3)

計算信息增益率CainRatio(GR)時，將計算香農熵的過程替換為計算Tsallis熵的過程，則信息增益率就轉變成了Tsallis信息增益率(TGR)。

當可調參數q→1時，TGR等價為基尼指數Gini。

(4)

調節不同的q，Tsallis熵退化為香農熵、信息增益率和基尼指數。因此，可以通過調節q的值來提高構建決策樹的性能。

2 關鍵度度量

決策樹葉節點的標識基于“少數服從多數”原則，在某些領域該原則能代表整體數據，但對分類問題，該原則忽略了一些少數但不可忽略的類別，或許這些類別才是更重要的。該問題出現的原因在于：對葉節點進行標識時只考慮到屬于葉節點j的樣本數據集，而并未考慮到總體樣本數據集。在訓練樣本集中，一些類Ai的樣本數量遠遠小于其他類別樣本數量，并在構建決策樹過程中該類別數據不斷被劃分到不同葉節點，最終在各樣本子集中，Aj類別的樣本數量占據較小比例。因此，使用關鍵度度量標準替代“少數服從多數”原則，不僅考慮當前葉節點中的各類樣本數據比例，也注重各類樣本總體數量，能完全解決小類屬被忽略的問題。

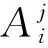
定義1 類分散度aij表示類Ai在節點j的分散程度，即節點j中Aj類樣本數量占總訓練樣本集中Ai的比例。

(5)

定義2 類決策度βij描述第i類樣本在節點j的權威性，即節點j中Ai類樣本數量占節點j中樣本數據的比例。

(6)

當建立完決策樹，對葉節點進行標識時時，綜合考慮aij和βij，βij表示當前類i的樣本在葉節點j中所占比例。未改進前，決策樹構建以βij為基礎按照“少數服從多數”的標準標識葉節點；改進后，不僅考慮βij，同時還將考慮aij，解決了小類屬無“話語權”的缺陷。當βij>0.8時，以類i標識葉節點j；當βij≤0.8時，使用關鍵度度量作為標識標準。

定義3 關鍵度度量dij為類分散度和類決策度的乘積，即

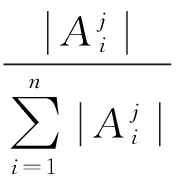
(7)

由式(6)(7)可知：aij和βij取值范圍均為[0，1]，因此dij取值范圍為[0，1]。當dij越接近1，則類i作為葉節點j的可能性越大；當dij=1時說明類i中所有樣本數據均分布在葉節點j，并且節點j中的類屬是純類。提出關鍵度度量后，為葉節點進行類標識時，選取關鍵度度量最大的類別，而不是選擇樣本數據最多的類別。

由上述可知：最終葉節點的標識類選取標準為

select(Ai)=arg max{dij}

(8)

對于表1，其類分散度和類決策度如表2所示。

表2 分散度和決策度

葉節點1：d11=a11β11=0.894 6，d21=a21β21=0.000 3

葉節點2：d12=a12β12=0.051 3，d22=a22β22=0.462 7

改進前，對表1中葉節點的類別標識以“少數服從多數”為標準。葉節點1以A1為標識，葉節點2以A2為標識。在本訓練樣本數據集中，A2屬于小類屬，被忽略掉。改進后，以“關鍵度度量”為標準，葉節點1中β11>0.8，所以葉節點1的類標識為A1；葉節點1中β11<0.8，A2類的關鍵度度量較大，所以葉節點2的類標識為A2，解決了小類屬屬性被忽略的缺陷。

3 基于Tsallis熵框架和關鍵度度量的決策樹構建

(9)

決策樹構建完成后，需要標識每個葉節點的類別，此時摒棄原始“少數服從多數”的原則，采用關鍵度度量的方式標識每個葉節點屬于哪種類別。遍歷所有葉節點，根據式(7)計算出每個葉節點中不同類別對應的關鍵度度量，由式(8)得到當前葉節點標識為關鍵度度量最大的類別。至此，決策樹構建完成。

4 實驗

本實驗分為兩部分：第1部分是在不同數據集上使用Tsallis框架和ID3、C4.5、CART算法形成決策樹，以這兩種決策樹為對測試樣本集進行分類，比較分類結果的準確度和樹規模，驗證本文基于Tsallis框架構建決策樹的性能；第2部分為在不同數據集上使用Tsallis框架構建決策樹時，引入“關鍵度度量”準則進行葉節點的標識，并在測試集上驗證準確度和決策樹規模，并與第1部分基于Tsallis框架構建決策樹進行比較。

4.1 基于Tsallis框架構建決策樹性能分析

在不同數據集上基于Tsallis框架和ID3、C4.5、CART算法構建決策樹并進行測試，比較準確度和決策樹規模。實驗數據采用UCI中Abalone數據集、Census Income數據集、Connect-4數據集、Image Segmentation 數據集、Mushroom數據集，決策樹構建過程同本文第3節，每組數據樣本包含的各類樣本數量均相同，因此避免了數據集中小類屬現象，得到5組測試結果，如表3所示。

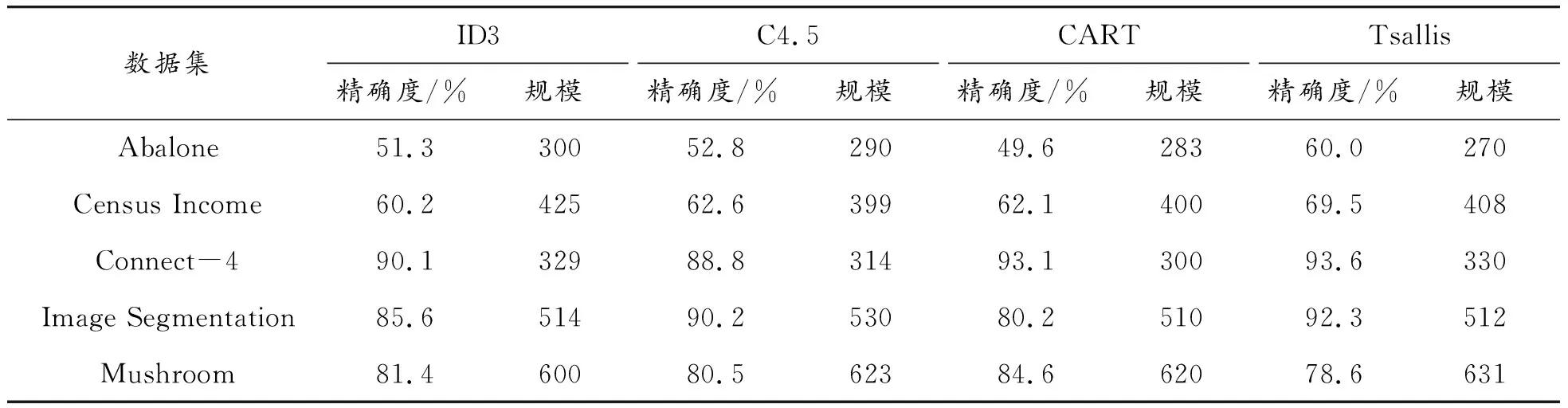
表3 基于Tsallis的決策樹

在Abalone數據集、Census Income數據集和Image Segmentation數據集上，采用C4.5分割算法構建決策樹準確度相對ID3和CART較好；在決策樹規模上，CART在Abalone數據集、Connect-4數據集和Image Segmentation數據集上性能好于ID3和C4.5分割算法。但是，基于Tsallis框架構建的決策樹，除Mushroom數據集外，準確度和樹規模上均好于其他3種經典算法，尤其是Abalone數據集，性能提高更加明顯。

4.2 基于Tsallis框架和關鍵度度量構建決策樹性能分析

在基于Tsallis框架構建決策樹的基礎上，以本文提出的“關鍵度度量”為基準標識葉節點，并在測試集上測試。其中，驗證部分仍采用10折交叉驗證法，但數據集中每類樣本數據不再均分到每組樣本，而是將數據集隨機分為10份，因此訓練數據集和測試樣本集中便會出現小類屬缺陷，目的為驗證本文提出的“關鍵度度量”標準，測試結果如表4所示。

表4 基于Tsallis框架和關鍵度度量的決策樹

對比表3和表4可知：出現小類屬屬性后的數據集，以Tsallis算法構建決策樹，準確性均有所下降，決策樹規模一定程度增大。當數據集中出現小類屬后，Tsallis仍以“少數服從多數”原則標識葉節點，因此小類屬分類被忽略后，在測試階段該類數據樣本被分錯類。當“關鍵度度量”取代“少數服從多數”標準后，在同樣的數據集上進行測試，準確度提高了，決策樹規模下降了，且相比本文1.2節基于Tsallis框架構建決策樹的性能也提高了。

4.3 不同參數q對構建決策樹的影響

本實驗采用UCI中Abalone數據集，該數據集有4 177個樣本實例，8個決策屬性，一個類別屬性，決策屬性中有1個離散屬性和7個連續屬性。調節q參數，調節范圍為[0.1，10.0]，q的變化梯度為0.1，對每個q驗證決策樹準確度和規模，將分類正確的樣本數量占測試集樣本數量的比重作為準確度。

實驗采用10折交叉驗證法，驗證構建決策樹的準確度和節點規模，整體Abalone數據集分為10組，每組數據集包含每類樣本均分的1/10，將其中任意9組樣本作為訓練集，剩余1組作為測試集，得到10組測試結果，求得10組準確度的平均值作為最終的準確度。不同q值在Abalone數據集上測試結果如圖1所示，圖1(a)是準確度，圖1(b)是決策樹規模。圖1(a)顯示：精確度對于參數q變化是敏感的，最高精確度在q=2.4處取得。圖1(b)顯示：決策樹規模對于參數q變化也是敏感的，最小決策樹規模在q=3.9處取得。最終，高精確度和低規模可以在q=1.7的位置取得。該實驗表明了參數q對決策樹精度和規模存在影響，在實際應用中可以根據精度和規模的側重點不同，調節q的取值。

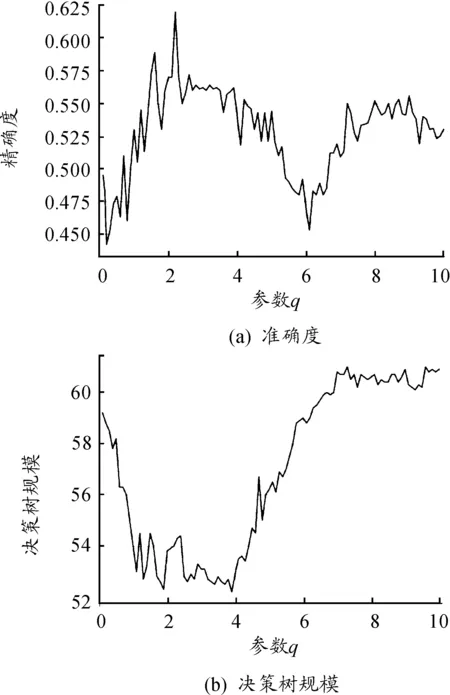
圖1 不同q值在Abalone數據集上的測試結果

5 結束語

本文對決策樹構建算法進行改進，提出Tsallis算法，將ID3、C4.5和CART統一起來，并通過調節q適應不同數據集，使Tsallis算法達到最優，同時結合“關鍵度度量”類標識標準，解決了數據集中小類屬被忽略的缺陷，以此方法構建的決策樹更加完美，不但準確度高，而且決策樹規模較小。實驗分為兩個部分：第1部分比較了Tsallis算法與傳統屬性分割方法構建決策樹準確度和樹規模，驗證了基于Tsallis算法構建決策樹性能的提高；第2部分在Tsallis算法基礎上引入了“關鍵度度量”并與Tsallis算法構建決策樹進行比較，準確度和樹規模均取得了更好的效果。經過兩部分的實驗，循序漸進地驗證了本文提出的改進措施，下一步研究重點為如何快速求得最佳參數q和進一步降低構建樹的時間復雜度。