貝塞爾曲線在浮式風(fēng)力機(jī)模型試驗(yàn)中的應(yīng)用

陳鳴芳，陳哲，何炎平，孟龍

（1.上海交通大學(xué)海洋工程國家重點(diǎn)實(shí)驗(yàn)室，上海 200240；2.高新船舶與深海開發(fā)裝備協(xié)同創(chuàng)新中心（船海協(xié)創(chuàng)中心），上海 200240；3.上海交通大學(xué)船舶海洋與建筑工程學(xué)院，上海 200240）

近年來，風(fēng)電行業(yè)得到進(jìn)一步發(fā)展。如2016年，國家發(fā)展改革委發(fā)布的《可再生能源發(fā)展“十三五”規(guī)劃》明確指出，要全面協(xié)調(diào)推進(jìn)風(fēng)電開發(fā)，到2020年底，風(fēng)電并網(wǎng)裝機(jī)確保達(dá)到2.1億千瓦以上。海上風(fēng)電由于來流穩(wěn)定、速度大，已逐漸成為重點(diǎn)發(fā)展方向。為更好的利用海上風(fēng)電資源，國內(nèi)科研院所積極開展不同形式的浮式風(fēng)力機(jī)模型試驗(yàn)。如上海交通大學(xué)海洋工程水池開展的TLP型浮式風(fēng)力機(jī)模型試驗(yàn)，哈爾濱工程大學(xué)海洋可再生能源實(shí)驗(yàn)室開展的Spar型浮式風(fēng)力機(jī)模型試驗(yàn)等。在浮式風(fēng)力機(jī)模型試驗(yàn)中，由于滿足弗汝德相似定律，試驗(yàn)產(chǎn)生較為嚴(yán)重的尺度效應(yīng)，導(dǎo)致幾何相似葉片產(chǎn)生的推力遠(yuǎn)小于目標(biāo)推力。為保證試驗(yàn)的準(zhǔn)確性，美國緬因大學(xué)Martin等在試驗(yàn)中嘗試對(duì)比多種消除尺度效應(yīng)的方法，提出重新設(shè)計(jì)模型葉片的方法可以較好的滿足試驗(yàn)要求。

本文以某6MW海上浮式風(fēng)力機(jī)模型試驗(yàn)為例，在弗汝德相似條件下，確定模型縮尺比為1：65.3。文章采用三次貝塞爾曲線定義模型葉片弦長和扭角沿展向分布，通過模式搜索法優(yōu)化曲線控制點(diǎn)坐標(biāo)得到滿足推力相似的模型葉片，并對(duì)多種試驗(yàn)工況進(jìn)行分析。

1 設(shè)計(jì)理論

1.1 葉素-動(dòng)量理論

本文采用葉素-動(dòng)量理論計(jì)算模型葉片推力。其基本思路是將葉片分為若干個(gè)有限微段，分別對(duì)每個(gè)微段進(jìn)行受力分析，最終確定整個(gè)葉片受力情況。對(duì)于單個(gè)微段，當(dāng)忽略相鄰葉素干擾時(shí)，可將其看作二維翼型，其受力情況如圖1所示。

根據(jù)動(dòng)量方程和葉素方程，通過迭代法確定每段葉素軸向和周向誘導(dǎo)因子，進(jìn)而求得葉素所處雷諾數(shù)大小。根據(jù)雷諾數(shù)和攻角數(shù)值，得到翼型升、阻力系數(shù)，確定葉素推力數(shù)值。最后，將所有葉素受到的風(fēng)輪推力疊加得到模型葉片推力。由于在模型葉片優(yōu)化設(shè)計(jì)中，葉素所處雷諾數(shù)和攻角數(shù)值隨著優(yōu)化過程不斷變化，為簡便計(jì)算，葉素升阻力系數(shù)建議采用低雷諾數(shù)升阻力系數(shù)圖譜確定。

圖1 葉素受力分析圖

1.2 貝塞爾曲線

貝塞爾曲線是法國工程師貝塞爾在1962年提出的，其形狀由曲線控制點(diǎn)確定，通過改變控制點(diǎn)位置可以實(shí)現(xiàn)曲線形狀的變化。其中，控制點(diǎn)起、終點(diǎn)與曲線的起、終點(diǎn)重合。

為保證模型葉片弦長和扭角沿展向連續(xù)分布，本文采用三次貝塞爾曲線定義弦長和扭角沿展向變化。三次貝塞爾曲線的參數(shù)公式為：

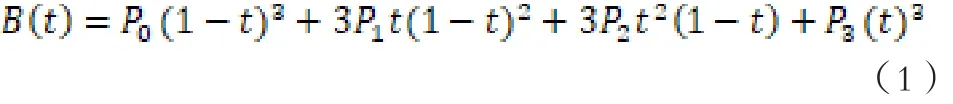
2 設(shè)計(jì)方法

2.1 葉片參數(shù)化表示

在模型葉片優(yōu)化設(shè)計(jì)中，首先需要確定優(yōu)化變量。試驗(yàn)任務(wù)書提供的原型葉片為離散數(shù)據(jù)，不利于葉片優(yōu)化設(shè)計(jì)，需要對(duì)葉片進(jìn)行參數(shù)化表達(dá)，以確定優(yōu)化變量。上海交通大學(xué)杜煒康等通過四次曲線和二次曲線分別表示葉片弦長和扭角沿展向變化。本文采用三次貝塞爾曲線定義模型葉片弦長和扭角沿展向分布，即在葉片展向位置分別定義4個(gè)控制點(diǎn)。其中，初始點(diǎn)為葉根處，終點(diǎn)為葉尖處，中間控制點(diǎn)分別布置在葉片距葉根37%和72%處，如圖2所示。

圖2 三次貝塞爾曲線定義幾何相似葉片弦長和扭角

2.2 葉片優(yōu)化設(shè)計(jì)

在葉片優(yōu)化設(shè)計(jì)中，保持曲線控制點(diǎn)沿展向位置不變，只改變控制點(diǎn)縱向坐標(biāo)實(shí)現(xiàn)曲線形狀的變化。其中，弦長和扭角曲線的起點(diǎn)和終點(diǎn)固定不動(dòng)，則優(yōu)化變量共有4個(gè)，即四點(diǎn)縱向坐標(biāo)值。以額定試驗(yàn)工況下目標(biāo)推力值為優(yōu)化設(shè)計(jì)目標(biāo)，通過模矢搜索法對(duì)4個(gè)變量進(jìn)行優(yōu)化，最終得到滿足目標(biāo)推力值的模型葉片，如圖3所示。

由圖3可知，優(yōu)化后，模型葉片弦長曲線控制點(diǎn)縱向坐標(biāo)增加，為弦長增大，且增大區(qū)域主要集中在葉片中部；扭角曲線控制點(diǎn)縱向坐標(biāo)減小，為扭角減小，減小區(qū)域主要集中在葉尖處。

3 對(duì)比分析

為更好的研究浮式風(fēng)力機(jī)性能，在模型試驗(yàn)中，需要對(duì)風(fēng)力機(jī)轉(zhuǎn)子在多種不同工況下進(jìn)行試驗(yàn)分析。本文根據(jù)模型試驗(yàn)任務(wù)書選取7種工況，對(duì)第2部分設(shè)計(jì)的模型葉片進(jìn)行計(jì)算分析，并與上海交通大學(xué)杜煒康等設(shè)計(jì)的模型葉片進(jìn)行對(duì)比，如圖4所示。

由圖可知，在額定工況下，貝塞爾曲線擬合法和多項(xiàng)式曲線擬合法均可得到滿足試驗(yàn)?zāi)繕?biāo)推力值的模型葉片。在其他工況下，貝塞爾曲線擬合法得到的模型葉片明顯優(yōu)于多項(xiàng)式曲線擬合法得到的葉片。

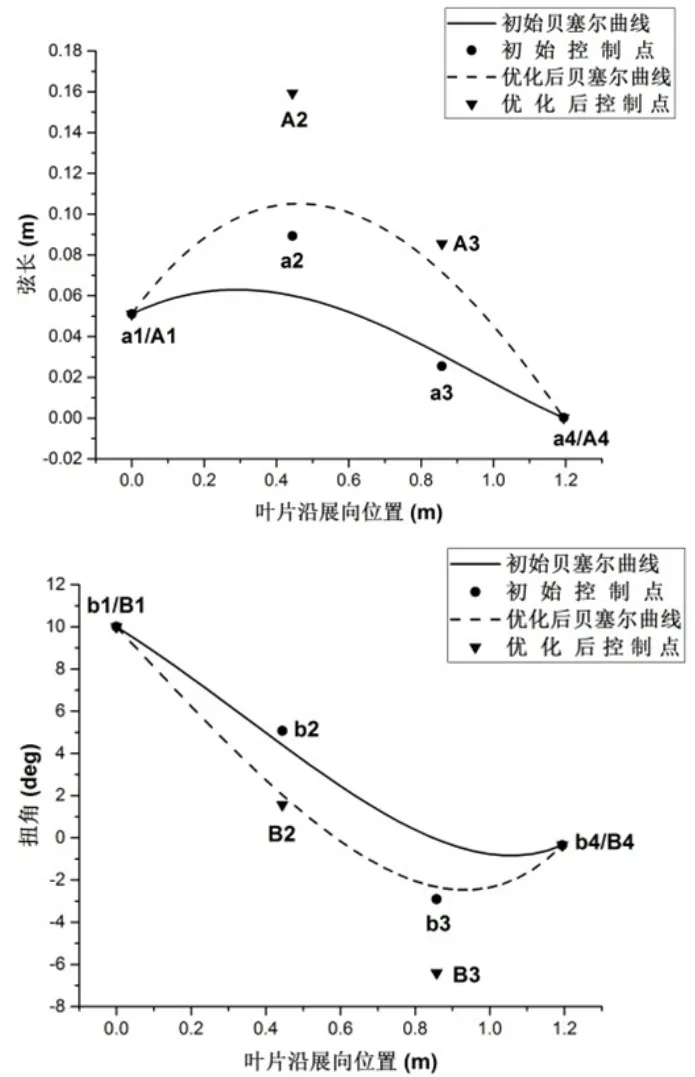
圖3 葉片弦長和扭角優(yōu)化前后對(duì)比

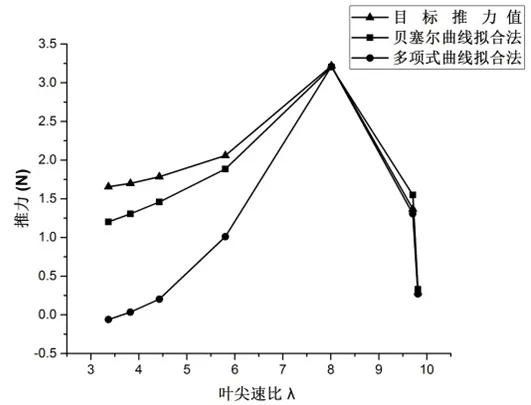
圖4 不同葉片推力數(shù)值對(duì)比

4 結(jié)語

（1）利用三次貝塞爾曲線定義模型葉片弦長和扭角沿展向分布情況，以額定工況下目標(biāo)推力值為優(yōu)化設(shè)計(jì)目標(biāo)，采用模式搜索法對(duì)模型葉片進(jìn)行優(yōu)化設(shè)計(jì)，得到滿足試驗(yàn)要求的模型葉片。

（2）與多項(xiàng)式曲線擬合得到的葉片對(duì)比分析，貝塞爾曲線擬合得到的葉片在其他試驗(yàn)工況下表現(xiàn)良好，具有較好的適應(yīng)性。