目標成本值最優的物聯網WSS蠕蟲抑制算法

黃一才 周偉偉 郁 濱

(解放軍信息工程大學 鄭州 450001) (huangyicai3698@163.com)

作為互聯網的發展與延伸，物聯網技術將廣泛應用于社會的方方面面[1-3].依據數據采集及傳輸方式，物聯網可分為有線服務系統和無線服務系統(wireless service system, WSS).物聯網WSS的實質是將最新的信息處理與通信技術進行有效的整合，利用各種感知設備和智能物體采集語音、圖像、位置等數據信息，并通過無線通信方式將采集到的信息傳遞到資源平臺進行云計算、數據挖掘等操作后，將處理與控制結果呈現給各用戶終端[4-6].然而，由于WSS需要將大量感知設備和物體連接到應用系統中，而且這些設備和物品信息大多采用資源受限的無線傳感器網絡節點進行傳輸，這在增加系統靈活性和方便性的同時，為蠕蟲在網絡中的大規模傳播提供了便利條件[7].蠕蟲可以竊取被感染節點的隱私數據和敏感信息，同時偽造身份向鄰居節點發送包含惡意代碼的無線再編程指令，使感染蠕蟲的節點數量不斷增加.被感染節點可能導致系統大面積數據阻塞甚至癱瘓.感知設備中嵌入的大多數無線傳感器節點具有資源有限的特性，如何最大限度地防御蠕蟲在系統中的傳播成為物聯網快速發展的關鍵.目前，針對無線網絡中蠕蟲的研究主要是利用傳統的流行病模型構建傳播體系[8]，在此基礎上，分析不同網絡參數對傳播速率的影響[9].

許多分布式網絡中的蠕蟲傳播及抑制方案這些年被相繼提出以保護采集數據的安全性和隱私性.有線網絡中經典的Kermack-Mckendrick參考模型將節點劃分為3種不同的狀態，利用控制參數和動力學微分方程描述蠕蟲的傳播速率，但僅將節點狀態假設為易感狀態，感染狀態和恢復狀態與WSS中IEEE 802.15.4協議不符[10].基于Markov鏈的傳播模型通過引入節點半徑與信道掃描的速率等參量求解各狀態變量的微分博弈方程，但該方法未考慮WSS中基站控制節點休眠和喚醒轉換概率的情況[11].基于細胞自動機的傳播模型對多跳廣播協議中的蠕蟲病毒傳播特點進行了模擬，但并未給出具體的防御和抑制方案[12].Bradley等人[13]提出了一種基于進程代數的復合主動蠕蟲傳播模型，通過PEPA流近似方法求解各狀態的常微分方程.但該模型需要消耗大量系統資源，并不適用于節點資源受限的WSS.基于分層結構的異構網絡蠕蟲傳播模型Enhanced-AAWP利用本地優先掃描蠕蟲和隨機掃描蠕蟲等方法研究蠕蟲的滲透傳播過程[14].由于傳統蠕蟲傳播模型中未考慮設備節點失效和休眠狀態，因此，現有傳播機制的分類并不適用于WSS.

高效的蠕蟲分類機制是提高蠕蟲傳播模型準確性和防御策略效率的重要因素.為解決現有蠕蟲分類準確性差的問題，朱克楠等人[15]基于樸素貝葉斯機器學習提出了利用行為序列報告和操作相似度窗口對蠕蟲進行自動分類的方法.該方法為WSS蠕蟲傳播及抑制模型的進一步研究提供了有力支撐.

上述方案僅利用各種傳播模型對蠕蟲在不同網絡環境下的傳播特點和分類方法進行了分析，依據動力學原理獲取不同節點的數據集，并未研究如何基于傳播規律建立動態防御策略集抑制蠕蟲在WSS中的傳播.

快速準確的蠕蟲檢測方法是實現WSS動態最優策略防御的基礎.近年來，一些學者通過降低噪聲和網絡隨機事件的干擾，提出了許多基于行為序列的檢測算法.毛蔚軒等人[16]利用節點休眠狀態和基于人工經驗的自適應學習方法，在分析網絡拓撲中各層節點數據流依賴關系的基礎上，給出了一種進程調用行為相似性與異常度結合的蠕蟲抑制算法.該算法保證在已知少量蠕蟲樣本的條件下得到理想的檢測率.文獻[17]提出基于平均場法建立免疫模型，但該模型的抑制策略中沒有休眠模式.針對混淆蠕蟲攻擊難以檢測的問題，馬洪亮等人[18]提出利用遍歷抽象語法樹(abstract syntax tree, AST)和單等級支持向量機(one class support vector machine, OC-SVM)檢測混淆并跟蹤節點相關的變量終值檢測反混淆.Das等人[19]用頻繁項離群確定同源度，并對同源判定閾值進行預定義，進而實現蠕蟲的同源判定.郭洋河等人[20]將數據和行為依賴關系相結合，提出了一種基于造價序列庫的蠕蟲識別機制.文獻[21-22]利用掛鉤API的方法追蹤外部節點的訪問行為，改善了動態檢測方法執行路徑單一的問題.這些檢測方法對蠕蟲的檢測成功率較高，但缺少與WSS匹配的蠕蟲最優防御算法.

在現有的蠕蟲檢測策略條件下，如何設計最優防御算法是WSS在高安全領域應用的關鍵.文獻[23]指出可以將蠕蟲防御問題轉化為動態博弈納什均衡的求解問題.Mishra等人[24]引入攻擊方的類型概率和收益矩陣，通過判斷貝葉斯博弈中收益函數值選取最優動作集合，但該方案不能實時校正外部節點的后驗概率.Pandey等人[25]將蠕蟲和系統的攻擊防御轉化為二者的最優化博弈問題，提出基于僵尸網絡環境的流行病模型以及微分博弈機制，在考慮防御策略及惡意軟件參數限制的基礎上給出了動態博弈的閉環納什均衡解.該方案雖然得到了微分博弈最優解，但未討論隔離狀態對其他網絡狀態的影響.這些方案雖然對蠕蟲在無線網絡中的傳播及抑制進行了一定程度的研究，但并未考慮WSS中基站能夠使易感節點免疫，同時可以廣播補丁程序治愈已感染節點.

結合WSS中的網絡參數及節點狀態特點，仍需重新建立傳播模型及基于時間特性的動態微分博弈模型，在滿足網絡參數約束條件的情況下，有效抑制蠕蟲在網絡中的傳播并使系統的安全成本最低.

本文的貢獻是構建一個描述物聯網WSS蠕蟲傳播規律的流行病模型和蠕蟲防御動態微分博弈模型，求解最優策略控制集合的取值并給出了抑制蠕蟲傳播的防御算法.具體地，本文主要得到3個方面的結果：

1) 依據物聯網中WSS的網絡拓撲結構，對蠕蟲攻擊下設備節點之間的狀態轉換過程進行分析，給出了WSS狀態轉換圖和各狀態微分方程，利用通信半徑確定具有感染能力的節點區域和數量并構建改進的流行病模型.

2) 建立蠕蟲和WSS間的動態微分博弈模型，通過目標成本函數量化攻擊方和防御方不同決策所得到的成本支付.

3) 利用漢密爾頓函數、瞬時成本函數以及終期成本函數的線性條件證明了動態微分博弈鞍點的存在性.結合成本函數與漢密爾頓函數的最小化極值特點，求解蠕蟲傳播的最優防御策略并給出了具體算法.

1 基礎知識

1.1 WSS系統結構

隨著物聯網在各個領域的快速發展，其安全問題越來越受到重視，尤其是對信息安全性和隱私性要求較高的WSS中.WSS大多采用無線傳感器網絡技術實現各節點之間的數據與圖像傳輸、數據處理、實時控制等.無線信道的開放性和節點的同構性使惡意軟件很容易在網絡中大面積傳播.

物聯網WSS的系統結構如圖1所示.該系統的目標是保證無論何時、何地、任何媒體設備的實時連通性和可控性.其結構主要包括無線傳輸系統、數據采集系統和終端用戶系統.由于WSS設備的移動性和采集數據分布范圍廣的特點，無線傳感器網絡技術在WSS數據采集和傳輸中的應用較為普遍.但嵌入無線傳感器網絡節點的設備一旦被蠕蟲感染，極易在網絡中傳播.這些被感染的節點對系統數據的機密性、隱私性和完整性構成了巨大威脅.

Fig. 1 System structure of WSS in IoT圖1 物聯網WSS的系統結構

1.2 網絡鏈路模型

(1)

節點間存在鏈接的概率p(da b)由WSS中的無線電通信機制以及節點間的通信半徑決定.信號發射端與信號接收端通過閾值判定模型確定節點間是否存在通信鏈路[26].

1.3 傳統流行病模型

流行病模型最早是用于預測和描述具有傳染性因素特征的部分人員集合隨時間實時變化的態勢.這些因素特征包括網絡節點的發送率、接收率、傳播速率等.依據不同網絡的特點，現有流行病模型分為SI[27]，SIS[28]，SIR[29]模型.

通常情況下，網絡中感染節點注入安全補丁可以轉變為恢復狀態.因此，SIR模型更適用于具有安全補丁的網絡流行病傳播特點.S(t)，I(t)，R(t)分別代表在時刻t易感節點、感染節點和免疫節點的數量.假設網絡中各節點之間存在通信鏈路，令α為蠕蟲感染速率，β為免疫速率，則描述各狀態節點變化速度的微分方程為

分析其他網絡模型時，可以依據經典SIR模型和具體的網絡協議進行分析和求解.

1.4 蠕蟲攻擊模型

WSS中傳播的蠕蟲主要指被動型蠕蟲.假設WSS中源節點的安全認證機制失效，蠕蟲控制該節點并獲取認證密鑰.感染節點利用簽名密鑰對嵌入蠕蟲字段的再編程命令幀簽名并發送到鄰居節點.其他鄰居節點收到偽裝的命令幀后驗證認證機制，更新配置并執行相應操作.蠕蟲在WSS節點間通過多跳的形式向外傳播.感染節點采集和傳輸的數據遭受竊聽、篡改和破壞.

2 WSS系統模型

2.1 狀態轉換

WSS中的蠕蟲傳播可以用包含易感節點、感染節點和免疫節點的區域來表示.不同狀態節點的分布如圖2所示.由于免疫節點在全網均勻分布，因此，未在系統模型中標出.

Fig. 2 System model of WSS圖2 WSS系統模型

Fig. 3 State transition diagram of nodes in WSS圖3 WSS節點狀態轉換圖

依據WSS的特點，節點可分為8種不同的狀態，各狀態之間的轉換關系如圖3所示:

1)S.處于狀態S的節點為易感節點，即易遭受蠕蟲感染，但目前仍處于正常工作狀態.

2)S1.處于狀態S1的節點是狀態S的休眠節點，由于節點處于休眠狀態時停止收發數據，該狀態的節點不會被蠕蟲感染.

3)I.處于狀態I的節點為感染節點，蠕蟲可以竊取節點存儲、處理、傳輸的數據，同時能通過該節點感染其他易感節點.

4)I1.處于狀態I1的節點為感染節點I的休眠節點，該狀態的節點失去通信功能，無法感染其他易感節點.

5)Q.處于狀態Q的節點為系統通過安全規則檢測并隔離的節點，該狀態的節點無法感染其他易感節點.

6)R.處于狀態R的節點為植入安全補丁后獲得對蠕蟲免疫狀態的節點.

7)R1.處于狀態R1的節點為狀態R的休眠節點.

8)D.處于狀態D的節點為失效節點，節點失去通信和數據處理功能.

8種不同狀態的節點滿足：

N=S(t)+I(t)+R(t)+S1(t)+
I1(t)+R1(t)+D(t)+Q(t).

(2)

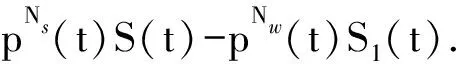
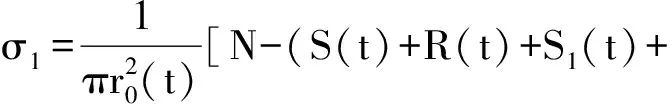
(3)

(4)

(5)

(6)

(7)

(8)

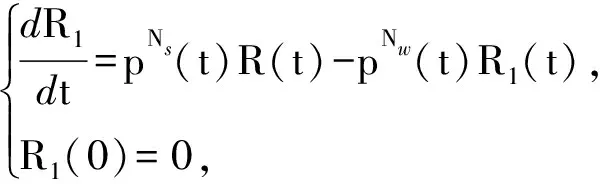
(9)

(10)

(11)

2.2 博弈模型

1)N={蠕蟲A，WSSD}是一個包含2個參與者的集合；

3)F={f(t,r(t),m(t),s(t))|fS,fI,fR,fS1,fI1,fR1,fQ,fD}，其中f(t,r(t),m(t),s(t))是一個隨時間連續變化的狀態函數，r(t)=(S(t),I(t),R(t),S1(t),I1(t),R1(t),Q(t),D(t))是一個8維的狀態變量，其中，

在定義1中，博弈雙方分別為蠕蟲A和WSSD，WSS通過調整防御策略S使目標成本函數J的值達到最小，而蠕蟲通過攻擊策略M保證J的值達到最大，該博弈模型為動態完全信息零和微分博弈，即攻擊方和防御方均知道對方采取每個策略的支付.

J(m(t),s*(t))≤J(m*(t),s*(t))≤J(m*(t),s(t)).

令V=J(m*(t),s*(t))，當攻擊方選擇策略m*(t)時，無論防御方采取何種防御措施，成本函數的值至少為V；當防御方采取策略s*(t)時，成本函數的值至多為V.當系統采取鞍點策略時，滿足關系V=V0=V1.

由于成本函數J與WSS的QoS相關，被蠕蟲感染的節點數據的機密性和隱私性遭到破壞，且影響節點的正常工作，節點持有的內部資源被非法調用和讀取，定義此時蠕蟲在感染節點集合中引起的瞬時成本為μII(t)，其中μI為協議中感染節點的瞬時成本相關系數.失效節點的增加會導致網絡中路由路徑發生改變，部分數據無法正常采集和傳遞，使成本函數值增加，由此，定義失效節點的瞬時成本為μDD(t),μD為失效節點的瞬時成本相關系數.同理可得,恢復節點的瞬時成本為μRR(t)，隔離節點的瞬時成本為μQQ(t)，休眠節點的瞬時成本函數分別為μS1S1(t)，-μI1I1(t)和μR1R1(t).

由以上分析可得，定義1中的成本函數可表示為

(12)

為了求解博弈K的鞍點策略，首先需要分析該博弈的鞍點是否存在.

定理1. 如果WSS中蠕蟲防御微分博弈滿足定義1及其約束條件，那么該博弈存在使系統達到最優的鞍點策略.

證明. 微分博弈存在鞍點策略必須滿足4個條件：

1) 系統的狀態函數在各狀態和控制策略上是連續且有界的；

2) 在成本函數中，瞬時成本和終期成本在各狀態和控制策略上是連續的；

3) 狀態函數和瞬時成本函數是由控制策略線性表示的，且博弈中定義的控制策略集合均是凸的；

4) 攻擊方和防御方的控制策略是有界的.

由定義1可知，狀態函數f(t,r(t),m(t),s(t))是連續的且其各狀態變量的取值由式(4)～(11)確定，M和S對控制策略的上下限進行約束，因此，狀態函數在各狀態和控制策略上是連續且有界的，條件1顯然滿足.瞬時成本和終期成本隨著各狀態和控制策略的增加而線性增加，其在各狀態和控制策略上是連續的，滿足條件2.由式(4)～(12)可知，狀態函數和瞬時成本函數均由控制策略線性表示，且控制策略集合中的參數可在連續區間內取值，故博弈中控制策略集合是凸的，滿足條件3.由協議中控制策略的約束條件可知，條件4顯然滿足.

因此，博弈K存在使系統性能達到最優的鞍點策略.

證畢.

3 博弈模型的求解

本節以動態微分博弈K的目標成本函數最小為求解依據，通過引入漢密爾頓函數，將目標成本函數最小問題轉化為判定雙方策略參數對應系數的正負問題.在此基礎上，結合狀態函數和初始狀態值，求解不同系數范圍下的最優控制策略.

由于參與者雙方的控制策略參數取值是一個連續的取值空間，博弈模型的最優策略求解無法通過線性分析和分類數值對比實現，且參數取值的無限特性使函數的凸性分析無法直接求解.因此，引入漢密爾頓函數作為對目標成本函數和各策略控制參數進行定量分析的工具，簡化最優控制策略的求解問題.

由于動態博弈存在鞍點策略，可以利用目標成本函數的性能泛函構建漢密爾頓函數，其協狀態函數可表示為

κ(t)=(κS(t)κI(t)κR(t)κS1(t)κI1(t)
κR1(t)κQ(t)κD(t))T.

利用拉格朗日乘子法，構造新的增廣泛函：

(13)

其中，κ(t)為8維的拉格朗日乘子系數矢量.純量函數H可表示為

H[t,κ(t),r(t),m(t),s(t)]=w(t,r(t),m(t),s(t))+
κ(t)f(t,r(t),m(t),s(t)).

(14)

H[t,κ(t),d(t),m(t),s(t)]為構造的漢密爾頓函數，則式(13)可簡化為

(15)

(16)

由式(15)展開歐拉方程可導出上述泛函極值的必要條件為

由式(12)和式(14)可得漢密爾頓函數如式(16)所示.

設漢密爾頓函數中各策略控制參數的系數分別為

可得：

(17)

依據漢密爾頓函數以及泛函極值的必要條件，可得協狀態函數的微分方程及極值，進而結合相應的初始條件得到協狀態函數κ(t)中的8個空間向量值，將其代入到式(17)可求解各策略控制參數的系數.

定理2. 如果蠕蟲與WSS之間的微分博弈滿足定義1，那么在動態微分博弈K中攻擊方蠕蟲A的最優控制策略為

防御方WSSD的最優控制策略為

證明. 由于漢密爾頓函數可表示為策略控制參數與相應系數的線性表達式，且泛函極值的必要條件中要求WSS中蠕蟲動態防御最優策略的鞍點必須滿足：

因此，當WSS策略控制參數相應的系數大于0時，策略控制參數取約束范圍內的最小值，反之取最大值.當蠕蟲策略控制參數相應的系數大于0時，策略控制參數取約束范圍內的最大值，反之取最小值.

證畢.

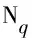
4 動態防御最優策略算法

依據第l個博弈階段的狀態節點數量初始值、狀態函數、協狀態函數以及各控制策略系數，由協議計算使蠕蟲動態防御最優的鞍點策略.該防御機制主要包括4個部分：參數存儲模塊(parameters storage module)、安全管理中心(security manage-ment center)、蠕蟲A(wormA)、WSSD.在此基礎上，設計適應于WSS的蠕蟲動態防御最優策略機制如圖4所示:

Fig. 4 Optimal defense strategy against worm propagation based on modified epidemic model圖4 基于改進流行病模型的蠕蟲動態防御最優策略機制

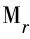
本方案中基于目標成本值最優的蠕蟲傳播最優攻擊算法和最優防御算法如下：

算法1. WSS蠕蟲傳播最優攻擊算法.

Step1. 初始化式(4)～(11)的假設條件，設置時間窗t=1，判斷是否滿足t≤k.若滿足條件，則利用狀態微分方程求解該博弈階段的各狀態值；否則跳轉到Step5.

Step2. 結合攻擊方和防御方控制參數初始值以及協狀態微分方程，將時刻lT0的協狀態值代入求解不同博弈階段的協狀態值κS(t),κI(t),κR(t),κS1(t),κI1(t),κR1(t),κQ(t),κD(t).

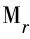
算法2. WSS蠕蟲傳播最優防御算法.

輸入：控制參數初始值及博弈階段起點t=1；

Step1. 設置初始時間窗t=1，配置初始化參數并由狀態微分方程求解各博弈階段狀態值，判斷是否滿足t≤k，若滿足執行下一步操作；否則跳轉到Step5.

Step2. 加載博弈中參與者的控制參數初始值以及協狀態微分方程，將時刻lT0的協狀態值代入求解不同博弈階段的協狀態值.

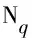
5 實驗與結果分析

5.1 實驗設計

本實驗在HP Z238工作站(3.2 GHz 8核心超線程、8 GB內存、Windows XP)上實現，使用的WSS網絡仿真平臺是NS-2，NS-2是由UC Berkeley開發的面向對象的無線網絡仿真模擬器.它通過設置虛擬時鐘并逐個執行離散事件完成算法的運行.從VXHeaven中抽取5個蠕蟲樣本并隨機選取一種作為WSS蠕蟲攻擊源.

Table 1 Parameter Configuration in NS-2表1 NS-2參數設置

NS-2配置細胞自動機算法[12]的類型為混沌型，采用諾伊曼細胞空間對網絡節點進行編號，節點i的狀態為Si∈{1,2,3,4,5,6,7,8}，該節點的2鄰居狀態分別為(Si-1,t)和(Si+1,t)，利用轉換規則函數表切換各節點狀態.

Enhanced-AAWP掃描算法[21]中蠕蟲實例的平均掃描速率為η=7，一個掃描時間單元的長度為60 s，系統采取隨機掃描和本地掃描的概率分別為P1=0.875和P2=0.125.

在上述網絡環境下運行細胞自動機算法[12]、Enhanced-AAWP掃描算法[21]和本文算法，利用NS-2中的State sniffer進程追蹤并統計各狀態節點以及策略參數的變化情況，結合MATLAB 2010a對實驗結果進行數值分析.通過仿真實驗對比這3種算法在WSS蠕蟲防御方面的性能差異.

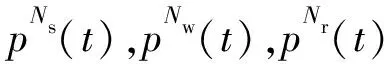
5.2 方案性能測試

通過仿真環境實現文獻[12,21]中的方案及初始條件，對比不同狀態節點所占比例隨時間的變化曲線.為了得到更加精確的結果，重復實驗20次并取所有結果的平均值.

如圖5所示，在文獻[21]中，網絡模型通過Enhanced-AAWP隨機掃描和本地掃描蠕蟲，未考慮休眠節點和隔離節點對策略均衡的影響，導致在計算防御策略的閾值時存在較大誤差，S和I的實驗測定值與文獻[21]中均衡方程的計算值誤差超過6%.在第1個博弈階段，算法中防御參數的切換延遲，易感節點所占的比例迅速下降.感染節點所占比例在第43個博弈階段達到最大值.隨著恢復節點所占比例的增加，感染節點縮小對周圍節點發送蠕蟲命令幀的數據量，開始執行使感染節點轉變為失效節點的策略.該方案在建立脆弱性主機自治系統的全局可達網絡時假設狀態為I的節點均有蠕蟲傳播能力，而感染節點區域內距離外部易感節點距離超過Rc的感染節點不具備感染能力.在最終平衡態時易感節點的比例保持在2.19%～3.06%，由感染節點轉變為失效節點的比例為32.29%，方案的均衡策略不能達到實際的最優抑制效果.

Fig. 5 Fraction curve of nodes in each state of Ref [21]圖5 文獻[21]中各狀態節點曲線

與文獻[21]相比，文獻[12]在建立網絡模型時考慮了靠近感染節點區域內側時無法與外側易感節點通信的情況，但在流行病模型的計算中未引入休眠節點和隔離節點的微分方程.如圖6所示，易感節點所占比例在整個博弈階段明顯優于文獻[21].當博弈結束時，易感節點所占比例的穩態值7.69%大于文獻[21].感染節點所占比例的曲線波峰到來的時間遲于文獻[21].失效節點增加的速度有所減小，且穩態時所占比例保持在21.31%，低于Enhanced-AAWP中的32.29%，由于休眠節點和隔離節點對蠕蟲傳播具有抑制作用，該方案將這2種節點均作為易感節點進行數值計算，防御策略的參數取值時間不夠準確.失效節點和感染節點所占比例均超過18%.

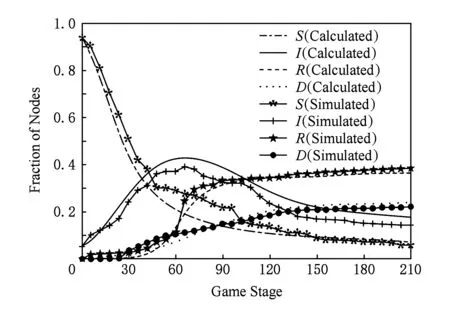
Fig. 6 Fraction curve of nodes in each state of Ref [12]圖6 文獻[12]中各狀態節點曲線

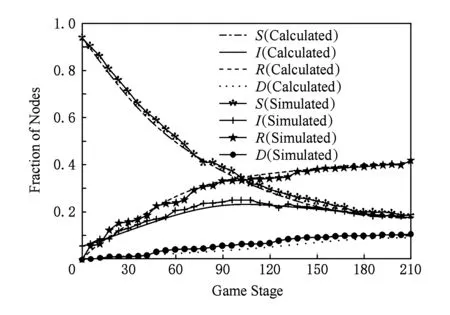
Fig. 7 Fraction curve of nodes in each state of this paper圖7 本文中各狀態節點曲線

本文方案中各狀態節點所占比例的理論值與仿真計算值如圖7所示.動態防御最優策略算法在S-I-R動力學模型的基礎上添加了休眠狀態(S1，I1，R1)以及安全隔離狀態(Q)，且利用Rc=50及式(3)計算了具備蠕蟲傳播能力的感染節點.易感節點在穩態時的比例保持在19.17%～20.62%，失效節點的比例在整個博弈階段低于10%，感染節點比例控制在17.29%～18.06%.感染節點的比例在第96個博弈階段時達到最大值22.17%，遠低于其他防御策略.從第96個博弈階段開始，基站向網絡中發送大量安全補丁，同時大量節點處于休眠狀態阻止蠕蟲在系統中的傳播，因此，恢復節點的比例并未迅速增長.與上述2種方案相比，改進流行病模型得到的鞍點策略在蠕蟲傳播方面具有更好的抑制效果.

State sniffer采集到的數據代入式(12)得到各算法目標成本值隨時間的變化情況，如圖8所示.I(0)=120的目標成本值不到I(0)=240的目標成本值的40%，這是由于達到均衡時I(t)和D(t)在目標成本值中所占比例

較大.隨著博弈階段的更新，當I(0)=120和I(0)=240時，本文算法在各階段達到策略均衡時的目標成本值均遠小于其他算法，且差值逐漸擴大.基于改進流行病模型和目標成本值最優的抑制算法在WSS蠕蟲傳播防御方面具有明顯優勢.

Fig. 8 Comparison of target costs in different strategies圖8 不同策略下的目標成本值對比

5.3 參數分析

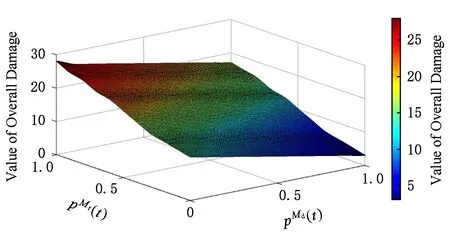
Fig. 9 Target cost under different and 圖9 不同和下的目標成本值

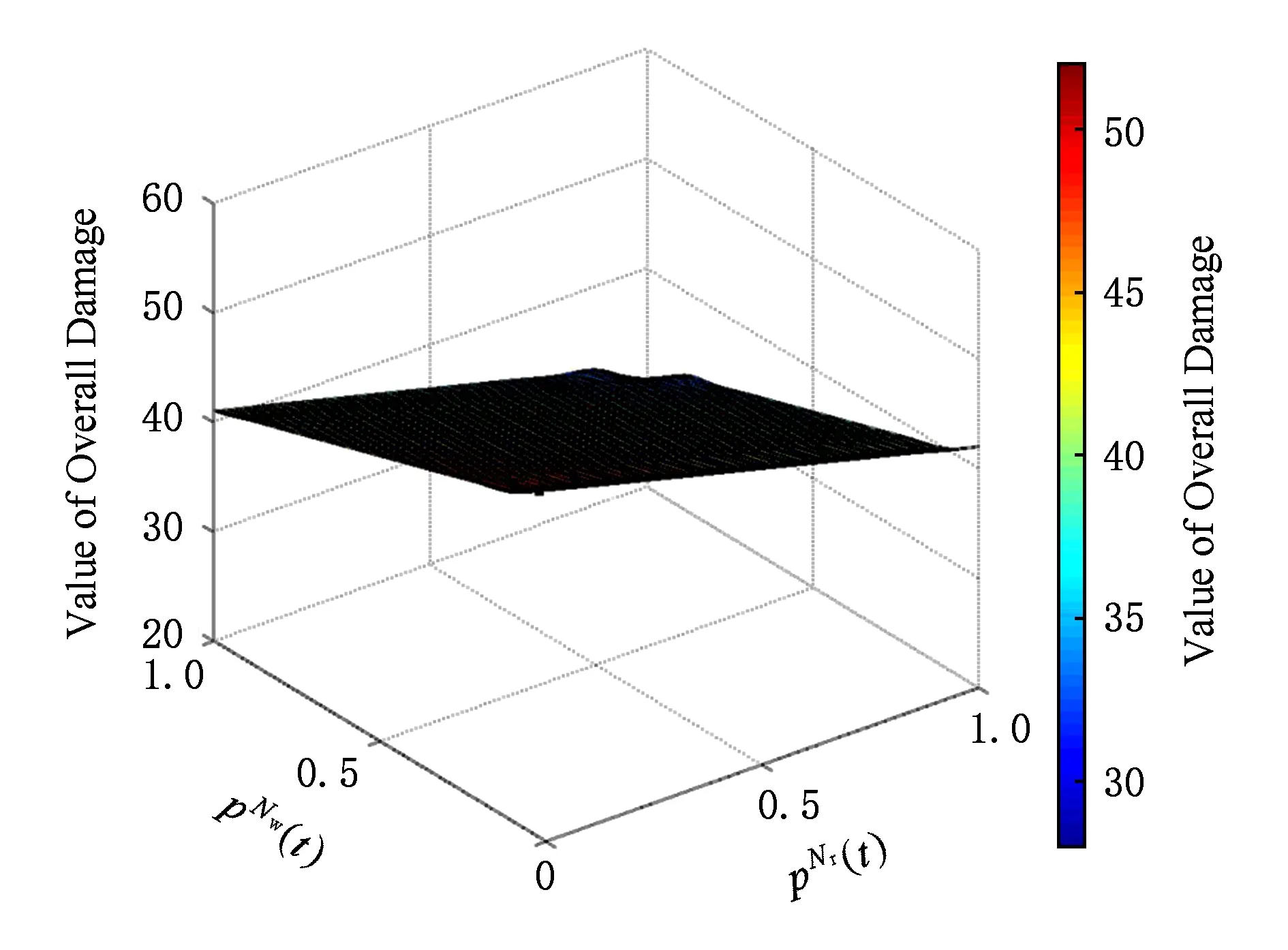
Fig. 10 Target cost under different and 圖10 不同和下的目標成本值

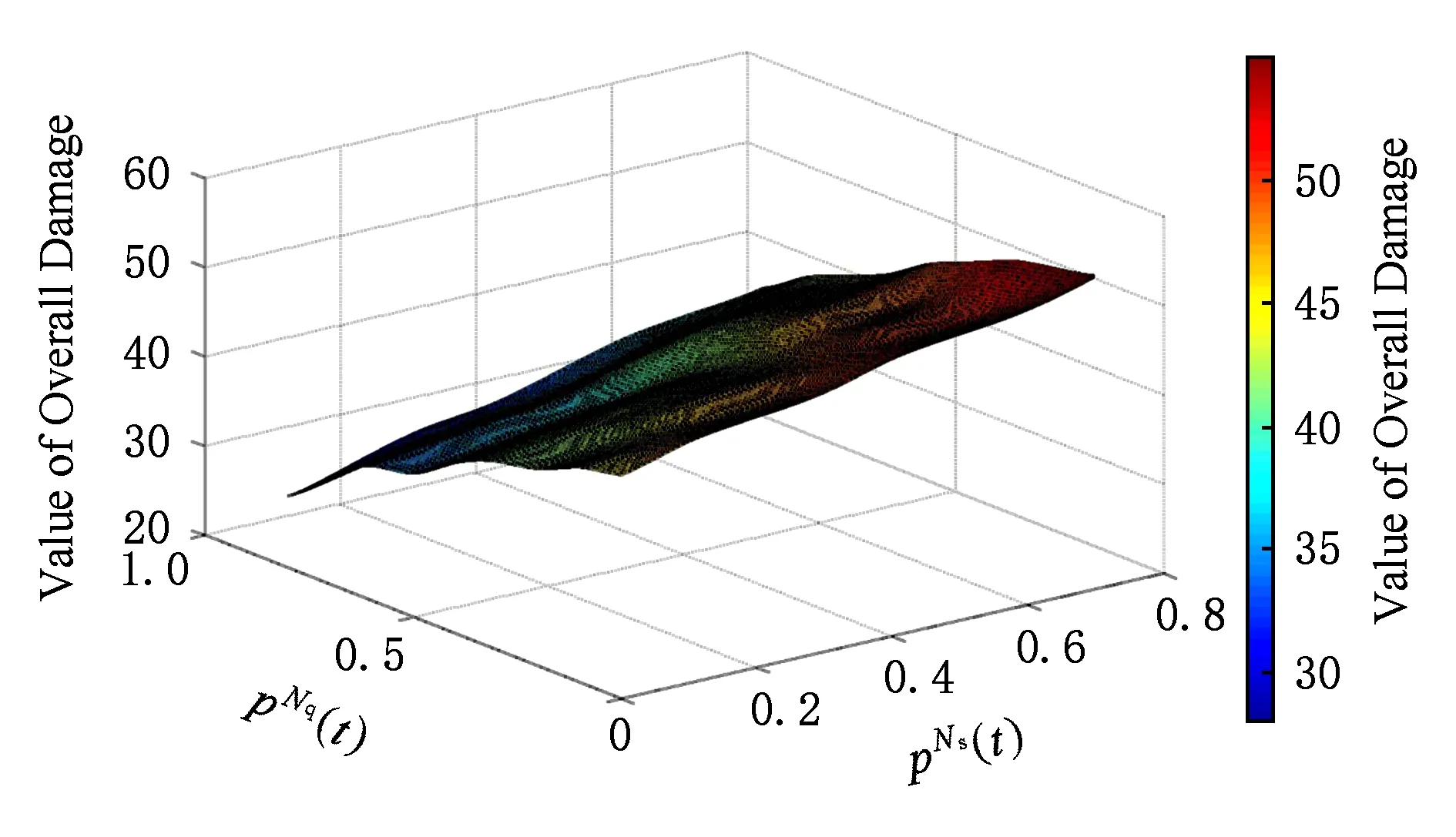
Fig. 11 Target cost under different and 圖11 不同和下的目標成本值

由圖9～11可知:本文中WSS蠕蟲傳播最優攻擊算法以及最優防御算法的控制參數取值相對于目標成本函數具有最優特性，即圖4中的方案在不同博弈階段的參數取值對攻擊者和防御者均為最優策略.基于目標成本值最優的蠕蟲傳播抑制算法可以最大限度地提高WSS的安全性能.

6 結束語

物聯網WSS中的蠕蟲傳播問題嚴重限制了其在工業生產、災害預警、智能管理等領域的應用.為了解決這一問題，自主研究具有最優特性的WSS蠕蟲傳播抑制算法.

本文提出了一種基于目標成本值最優的WSS蠕蟲傳播抑制算法，和其他同類型算法相比具有3個方面優點：

1)在傳統SIR模型的基礎上，引入休眠狀態和隔離狀態，建立了狀態轉換圖和改進的流行病模型，并給出了各狀態節點的微分方程及初始狀態，使不同博弈階段狀態節點數量的計算更加準確；

2)本文構建了蠕蟲傳播的系統模型，利用節點的通信半徑以及感染節點的分布規律，準確計算了具有蠕蟲傳播能力的感染節點數量，使感染節點的狀態微分方程對下一時刻狀態節點的預測更加精確；

3)本文建立了WSS和蠕蟲的動態微分博弈模型，以目標成本值最優作為鞍點策略的求解條件，通過狀態變量、協狀態變量以及漢密爾頓函數的線性特點實現均衡策略的求解，在此基礎上，提出了蠕蟲傳播抑制最優策略算法，與其他算法相比，本文算法在不同博弈階段狀態節點預測以及WSS蠕蟲傳播抑制方面具有明顯優勢.